Question 7. [Maximum mark: 5]
A function is defined by \(f (x) = 2 – \frac{12}{x+5}\) for −7 ≤ x ≤ 7, x ≠ −5.
a. Find the range of f . [3]
b. Find the value of f −1 [2]
Answer/Explanation
(a) (f(-7)=) 8 and (f(-7)=)1 range is f(x) ≤ 1, f (x) ≥ 8
(b) EITHER sketch of f and y = 0 or sketch of f−1 and \(x = 0 \) OR
finding the correct expression of f−1 (x) =\(\frac{-2-5x}{x-2}\) OR
\(f^{-1}(0)=\frac{-2-5(0)}{x-2}\) OR
\(f (x) = 0\) THEN f−1 (0) =1
Question
Consider the numbers \(2\), \(\sqrt 3 \), \( – \frac{2}{3}\) and the sets \(\mathbb{N}\), \(\mathbb{Z}\), \(\mathbb{Q}\) and \(\mathbb{R}\).
Complete the table below by placing a tick in the appropriate box if the number is an element of the set, and a cross if it is not.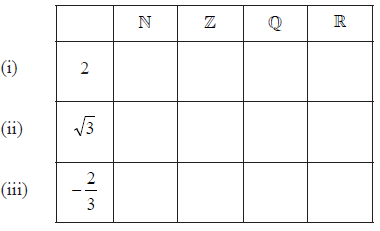
[3]
A function \(f\) is given by \(f(x) = 2{x^2} – 3x{\text{, }}x \in \{ – 2{\text{, }}2{\text{, }}3\} \).
Write down the range of function \(f\).[1]
Answer/Explanation
Markscheme
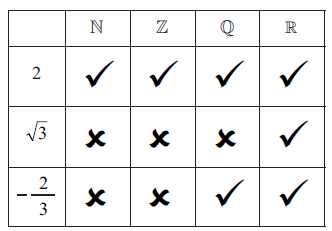(A1)(A1)(A1) (C3)
Note: Accept any symbol for ticks. Do not penalise if the other boxes are left blank.[3 marks]
\({\text{Range}} = \{ 2{\text{, }}9{\text{, }}14\} \) (A1)(ft) (C1)
Note: Brackets not required.[1 mark]
Question
Factorise the expression \({x^2} – 3x – 10\).[2]
A function is defined as \(f(x) = 1 + {x^3}\) for \(x \in \mathbb{Z}{\text{, }} {- 3} \leqslant x \leqslant 3\).
(i) List the elements of the domain of \(f(x)\).
(ii) Write down the range of \(f(x)\).[4]
Answer/Explanation
Markscheme
\((x – 5)(x + 2)\) (A1)(A1) (C2)
Note: Award (A1) for \((x + 5)(x – 2)\), (A0) otherwise. If equation is equated to zero and solved by factorizing award (A1) for both correct factors, followed by (A0).[2 marks]
(i) \( – 3\), \( – 2\), \( – 1\), \(0\), \(1\), \(2\), \(3\) (A1)(A1) (C2)
Note: Award (A2) for all correct answers seen and no others. Award (A1) for 3 correct answers seen.
(ii) \( – 26\), \( – 7\), 0,1, 2, 9, 28 (A1)(A1) (C2)
Note: Award (A2) for all correct answers seen and no others. Award (A1) for 3 correct answers seen. If domain and range are interchanged award (A0) for (b)(i) and (A1)(ft)(A1)(ft) for (b)(ii).[4 marks]
Question
The graph of a quadratic function \(y = f (x)\) is given below.
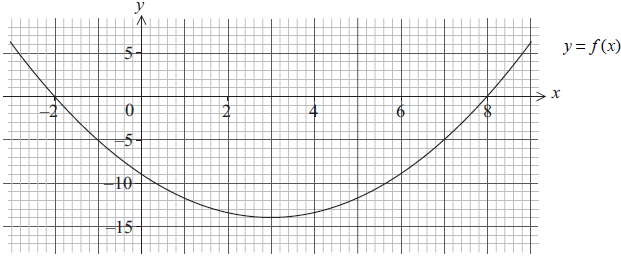
Write down the equation of the axis of symmetry.[2]
Write down the coordinates of the minimum point.[2]
Write down the range of \(f (x)\).[2]
Answer/Explanation
Markscheme
x = 3 (A1)(A1) (C2)
Notes: Award (A1) for “ x = ” (A1) for 3.
The mark for x = is not awarded unless a constant is seen on the other side of the equation.[2 marks]
(3, −14) (Accept x = 3, y = −14) (A1)(ft)(A1) (C2)Note: Award (A1)(A0) for missing coordinate brackets.[2 marks]
y ≥ −14 (A1)(A1)(ft) (C2)
Notes: Award (A1) for y ≥ , (A1)(ft) for –14.
Accept alternative notation for intervals.[2 marks]
Question
Given the function \(f (x) = 2 \times 3^x\) for −2 \( \leqslant \) x \( \leqslant \) 5,
find the range of \(f\).[4]
find the value of \(x\) given that \(f (x) =162\).[2]
Answer/Explanation
Markscheme
\(f (-2) = 2 \times 3^{-2}\) (M1)
\(= \frac{{2}}{{9}}(0.222)\) (A1)
\(f (5) = 2 \times 3^5\)
\(= 486\) (A1)
\({\text{Range }}\frac{2}{9} \leqslant f(x) \leqslant 486\) OR \(\left[ {\frac{2}{9},{\text{ }}486} \right]\) (A1) (C4)
Note: Award (M1) for correct substitution of –2 or 5 into \(f (x)\), (A1)(A1) for each correct end point.[4 marks]
\(2 \times 3^x = 162\) (M1)
\(x = 4\) (A1) (C2)[2 marks]