Question
Consider the functions \(f(x) = \frac{{2x + 3}}{{x + 4}}\) and \(g(x) = x + 0.5\) .
Sketch the graph of the function \(f(x)\), for \( – 10 \leqslant x \leqslant 10\) . Indicating clearly the axis intercepts and any asymptotes.[6]
Write down the equation of the vertical asymptote.[2]
On the same diagram as part (a) sketch the graph of \(g(x) = x + 0.5\) .[2]
Using your graphical display calculator write down the coordinates of one of the points of intersection on the graphs of \(f\) and \(g\), giving your answer correct to five decimal places.[3]
Write down the gradient of the line \(g(x) = x + 0.5\) .[1]
The line \(L\) passes through the point with coordinates \(( – 2{\text{, }} – 3)\) and is perpendicular to the line \(g(x)\) . Find the equation of \(L\).[3]
Answer/Explanation
Markscheme
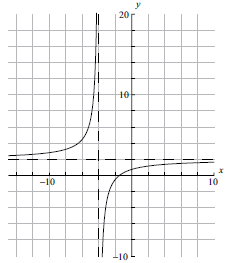(A6)
Notes: (A1) for labels and some idea of scale.
(A1) for \(x\)-intercept seen, (A1) for \(y\)-intercept seen in roughly the correct places (coordinates not required).
(A1) for vertical asymptote seen, (A1) for horizontal asymptote seen in roughly the correct places (equations of the lines not required).
(A1) for correct general shape.[6 marks]
\(x = – 4\) (A1)(A1)(ft)
Note: (A1) for \(x =\), (A1)(ft) for \( – 4\).[2 marks]
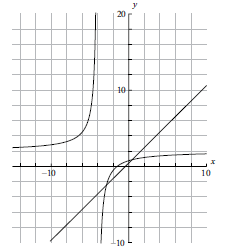(A1)(A1)
Note: (A1) for correct axis intercepts, (A1) for straight line[2 marks]
\(( – 2.85078{\text{, }} – 2.35078)\) OR \((0.35078{\text{, }}0.85078)\) (G1)(G1)(A1)(ft)
Notes: (A1) for \(x\)-coordinate, (A1) for \(y\)-coordinate, (A1)(ft) for correct accuracy. Brackets required. If brackets not used award (G1)(G0)(A1)(ft).
Accept \(x = – 2.85078\), \(y = – 2.35078\) or \(x = 0.35078\), \(y = 0.85078\).[3 marks]
\({\text{gradient}} = 1\) (A1)[1 mark]
\({\text{gradient of perpendicular}} = – 1\) (A1)(ft)
(can be implied in the next step)
\(y = mx + c\)
\( – 3 = – 1 \times – 2 + c\) (M1)
\(c = – 5\)
\(y = – x – 5\) (A1)(ft)(G2)
OR
\(y + 3 = – (x + 2)\) (M1)(A1)(ft)(G2)
Note: Award (G2) for correct answer with no working at all but (A1)(G1) if the gradient is mentioned as \( – 1\) then correct answer with no further working.[3 marks]
Question
Mal is shopping for a school trip. He buys \(50\) tins of beans and \(20\) packets of cereal. The total cost is \(260\) Australian dollars (\({\text{AUD}}\)).
The triangular faces of a square based pyramid, \({\text{ABCDE}}\), are all inclined at \({70^ \circ }\) to the base. The edges of the base \({\text{ABCD}}\) are all \(10{\text{ cm}}\) and \({\text{M}}\) is the centre. \({\text{G}}\) is the mid-point of \({\text{CD}}\).
Write down an equation showing this information, taking \(b\) to be the cost of one tin of beans and \(c\) to be the cost of one packet of cereal in \({\text{AUD}}\).[1]
Stephen thinks that Mal has not bought enough so he buys \(12\) more tins of beans and \(6\) more packets of cereal. He pays \(66{\text{ AUD}}\).
Write down another equation to represent this information.[1]
Stephen thinks that Mal has not bought enough so he buys \(12\) more tins of beans and \(6\) more packets of cereal. He pays \(66{\text{ AUD}}\).
Find the cost of one tin of beans.[2]
(i) Sketch the graphs of the two equations from parts (a) and (b).
(ii) Write down the coordinates of the point of intersection of the two graphs.[4]
Using the letters on the diagram draw a triangle showing the position of a \({70^ \circ }\) angle.[1]
Show that the height of the pyramid is \(13.7{\text{ cm}}\), to 3 significant figures.[2]
Calculate
(i) the length of \({\text{EG}}\);
(ii) the size of angle \({\text{DEC}}\).[4]
Find the total surface area of the pyramid.[2]
Find the volume of the pyramid.[2]
Answer/Explanation
Markscheme
\(50b + 20c = 260\) (A1)[1 mark]
\(12b + 6c = 66\) (A1)[1 mark]
Solve to get \(b = 4\) (M1)(A1)(ft)(G2)
Note: (M1) for attempting to solve the equations simultaneously.[2 marks]
(i)
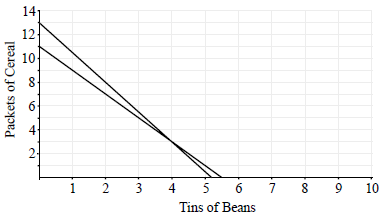(A1)(A1)(A1)
Notes: Award (A1) for labels and some idea of scale, (A1)(ft)(A1)(ft) for each line.
The axis can be reversed.
(ii) \((4,3)\) or \((3,4)\) (A1)(ft)
Note: Accept \(b = 4\), \(c = 3\)[4 marks]
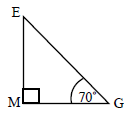(A1)[1 mark]
\(\tan 70 = \frac{h}{5}\) (M1)
\(h = 5\tan 70 = 13.74\) (A1)
\(h = 13.7{\text{ cm}}\) (AG)[2 marks]
Unit penalty (UP) is applicable in this part of the question where indicated in the left hand column.
(i) \({\text{E}}{{\text{G}}^2} = {5^2} + {13.7^2}\) OR \({5^2} + {(5\tan 70)^2}\) (M1)
(UP) \({\text{EG}} = 14.6{\text{ cm}}\) (A1)(G2)
(ii) \({\text{DEC}} = 2 \times {\tan ^{ – 1}}\left( {\frac{5}{{14.6}}} \right)\) (M1)
\( = {37.8^ \circ }\) (A1)(ft)(G2)[4 marks]
Unit penalty (UP) is applicable in this part of the question where indicated in the left hand column.
\({\text{Area}} = 10 \times 10 + 4 \times 0.5 \times 10 \times 14.619\) (M1)
(UP) \( = 392{\text{ c}}{{\text{m}}^2}\) (A1)(ft)(G2)[2 marks]
Unit penalty (UP) is applicable in this part of the question where indicated in the left hand column.
\({\text{Volume}} = \frac{1}{3} \times 10 \times 10 \times 13.7\) (M1)
(UP) \( = 457{\text{ c}}{{\text{m}}^3}\) (\(458{\text{ c}}{{\text{m}}^3}\)) (A1)(G2)[2 marks]
Question
Consider the function \(f:x \mapsto \frac{{kx}}{{{2^x}}}\).
The cost per person, in euros, when \(x\) people are invited to a party can be determined by the function
\(C(x) = x + \frac{{100}}{x}\)
Given that \(f(1) = 2\), show that \(k = 4\).[2]
Write down the values of \(q\) and \(r\) for the following table.
[2]
As \(x\) increases from \( – 1\), the graph of \(y = f(x)\) reaches a maximum value and then decreases, behaving asymptotically.
Draw the graph of \(y = f(x)\) for \( – 1 \leqslant x \leqslant 8\). Use a scale of \({\text{1 cm}}\) to represent 1 unit on both axes. The position of the maximum, \({\text{M}}\), the \(y\)-intercept and the asymptotic behaviour should be clearly shown.[4]
Using your graphic display calculator, find the coordinates of \({\text{M}}\), the maximum point on the graph of \(y = f(x)\).[2]
Write down the equation of the horizontal asymptote to the graph of \(y = f(x)\).[2]
(i) Draw and label the line \( y = 1\) on your graph.
(ii) The equation \(f(x) = 1\) has two solutions. One of the solutions is \(x = 4\). Use your graph to find the other solution.[4]
Find \(C'(x)\).[3]
Show that the cost per person is a minimum when \(10\) people are invited to the party.[2]
Calculate the minimum cost per person.[2]
Answer/Explanation
Markscheme
\(f(1) = \frac{k}{{{2^1}}}\) (M1)
Note: (M1) for substituting \(x = 1\) into the formula.
\(\frac{k}{2} = 2\) (M1)
Note: (M1) for equating to 2.
\(k = 4\) (AG)[2 marks]
\(q = 2\), \(r = 0.125\) (A1)(A1)[2 marks]
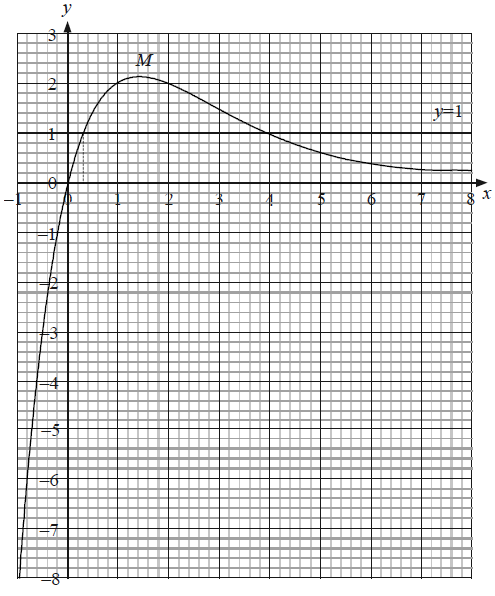(A4)
Notes: (A1) for scales and labels.
(A1) for accurate smooth curve passing through \((0, 0)\) drawn at least in the given domain.
(A1) for asymptotic behaviour (curve must not go up or cross the \(x\)-axis).
(A1) for indicating the position of the maximum point.[4 marks]
\({\text{M}}\) (\(1.44\), \(2.12\)) (G1)(G1)
Note: Brackets required, if missing award (G1)(G0). Accept \(x = 1.44\) and \(y = 2.12\).[2 marks]
\(y = 0\) (A1)(A1)
Note: (A1) for ‘\(y = \)’ provided the right hand side is a constant. (A1) for 0.[2 marks]
(i) See graph (A1)(A1)
Note: (A1) for correct line, (A1) for label.
(ii) \(x = 0.3\) (ft) from candidate’s graph. (A2)(ft)
Notes: Accept \( \pm 0.1\) from their x. For \(0.310\) award (G1)(G0). For other answers taken from the GDC and not given correct to 3 significant figures award (G0)(AP)(G0) or (G1)(G0) if (AP) already applied.[4 marks]
\(C'(x) = 1 – \frac{{100}}{{{x^2}}}\) (A1)(A1)(A1)
Note: (A1) for 1, (A1) for \( – 100\) , (A1) for \({x^2}\) as denominator or \({{x^{ – 2}}}\) as numerator. Award a maximum of (A2) if an extra term is seen.[3 marks]
For studying signs of the derivative at either side of \(x = 10\) (M1)
For saying there is a change of sign of the derivative (M1)(AG)
OR
For putting \(x = 10\) into \(C’\) and getting zero (M1)
For clear sketch of the function or for mentioning that the function changes from decreasing to increasing at \(x = 10\) (M1)(AG)
OR
For solving \(C'(x) = 0\) and getting \(10\) (M1)
For clear sketch of the function or for mentioning that the function changes from decreasing to increasing at \(x = 10\) (M1)(AG)
Note: For a sketch with a clear indication of the minimum or for a table with values of \(x\) at either side of \(x = 10\) award (M1)(M0).[2 marks]
\(C(10) = 10 + \frac{{100}}{{10}}\) (M1)
\(C(10) = 20\) (A1)(G2)[2 marks]
Question
Throughout this question all the numerical answers must be given correct to the nearest whole number.
Park School started in January 2000 with \(100\) students. Every full year, there is an increase of \(6\% \) in the number of students.
Find the number of students attending Park School in
(i) January 2001;
(ii) January 2003.[4]
Park School started in January 2000 with \(100\) students. Every full year, there is an increase of \(6\% \) in the number of students.
Show that the number of students attending Park School in January 2007 is \(150\).[2]
Grove School had \(110\) students in January 2000. Every full year, the number of students is \(10\) more than in the previous year.
Find the number of students attending Grove School in January 2003.[2]
Grove School had \(110\) students in January 2000. Every full year, the number of students is \(10\) more than in the previous year.
Find the year in which the number of students attending Grove School will be first \(60\% \) more than in January 2000.[4]
Each January, one of these two schools, the one that has more students, is given extra money to spend on sports equipment.
(i) Decide which school gets the money in 2007. Justify your answer.
(ii) Find the first year in which Park School will be given this extra money.[5]
Answer/Explanation
Markscheme
(i) \(100 \times 1.06 = 106\) (M1)(A1)(G2)
Note: (M1) for multiplying by \(1.06\) or equivalent. (A1) for correct answer.
(ii) \(100 \times {1.06^3} = 119\) (M1)(A1)(G2)
Note: (M1) for multiplying by \({1.06^3}\) or equivalent or for list of values. (A1) for correct answer.[4 marks]
\(100 \times {1.06^7} = 150.36 \ldots = 150\) correct to the nearest whole (M1)(A1)(AG)
Note: (M1) for correct formula or for list of values. (A1) for correct substitution or for \(150\) in the correct position in the list. Unrounded answer must be seen for the (A1).[2 marks]
\(110 + 3 \times 10 = 140\) (M1)(A1)(G2)
Note: (M1) for adding \(30\) or for list of values. (A1) for correct answer.[2 marks]
In (d) and (e) follow through from (c) if consistent wrong use of correct AP formula.
\(110 + (n – 1) \times 10 > 176\) (A1)(M1)
\(n = 8\therefore {\text{year 2007}}\) (A1)(A1)(ft)(G2)
Note: (A1) for \(176\) or \(66\) seen. (M1) for showing list of values and comparing them to \(176\) or for equating formula to \(176\) or for writing the inequality. If \(n = 8\) not seen can still get (A2) for 2007. Answer \(n = 8\) with no working gets (G1).
OR
\(110 + n \times 10 > 176\) (A1)(M1)
\(n = 7\therefore {\text{year 2007}}\) (A1)(A1)(ft)(G2)[4 marks]
In (d) and (e) follow through from (c) if consistent wrong use of correct AP formula.
(i) \(180\) (A1)(ft)
Grove School gets the money. (A1)(ft)
Note: (A1) for \(180\) seen. (A1) for correct answer.
(ii) \({\text{100}} \times {\text{1}}{\text{.0}}{{\text{6}}^{n – 1}} > 110 + (n – 1) \times 10\) (M1)
\(n = 20\therefore {\text{year 2019}}\) (A1)(A1)(ft)(G2)
Note: (M1) for showing lists of values for each school and comparing them or for equating both formulae or writing the correct inequality. If \(n = 20\) not seen can still get (A2) for 2019. Follow through with ratio used in (b) and/or formula used in (d).
OR
\(100 \times {1.06^n} > 110 + n \times 10\) (M1)
\(n = 19\therefore {\text{year 2019}}\) (A1)(A1)(ft)(G2)
OR
graphically
Note: (M1) for sketch of both functions on the same graph, (A1) for the intersection point, (A1) for correct answer.[5 marks]
Question
The temperature in \(^ \circ {\text{C}}\) of a pot of water removed from the cooker is given by \(T(m) = 20 + 70 \times {2.72^{ – 0.4m}}\), where \(m\) is the number of minutes after the pot is removed from the cooker.
Show that the temperature of the water when it is removed from the cooker is \({90^ \circ }{\text{C}}\).[2]
The following table shows values for \(m\) and \(T(m)\).
(i) Write down the value of \(s\).
(ii) Draw the graph of \(T(m)\) for \(0 \leqslant m \leqslant 10\) . Use a scale of \(1{\text{ cm}}\) to represent \(1\) minute on the horizontal axis and a scale of \(1{\text{ cm}}\) to represent \({10^ \circ }{\text{C}}\) on the vertical axis.
(iii) Use your graph to find how long it takes for the temperature to reach \({56^ \circ }{\text{C}}\). Show your method clearly.
(iv) Write down the temperature approached by the water after a long time. Justify your answer.[9]
Consider the function \(S(m) = 20m – 40\) for \(2 \leqslant m \leqslant 6\) .
The function \(S(m)\) represents the temperature of soup in a pot placed on the cooker two minutes after the water has been removed. The soup is then heated.
Draw the graph of \(S(m)\) on the same set of axes used for part (b).[2]
Consider the function \(S(m) = 20m – 40\) for \(2 \leqslant m \leqslant 6\) .
The function \(S(m)\) represents the temperature of soup in a pot placed on the cooker two minutes after the water has been removed. The soup is then heated.
Comment on the meaning of the constant \(20\) in the formula for \(S(m)\) in relation to the temperature of the soup.[1]
Consider the function \(S(m) = 20m – 40\) for \(2 \leqslant m \leqslant 6\) .
The function \(S(m)\) represents the temperature of soup in a pot placed on the cooker two minutes after the water has been removed. The soup is then heated.
(i) Use your graph to solve the equation \(S(m) = T(m)\) . Show your method clearly.
(ii) Hence describe by using inequalities the set of values of \(m\) for which \(S(m) > T(m)\).[4]
Answer/Explanation
Markscheme
\(T(0) = 20 + 70 \times {2.72^{ – 0.4 \times 0}} = 90\) (M1)(A1)(AG)
Note: (M1) for taking \(m = 0\) , (A1) for substituting \(0\) into the formula. For the A mark to be awarded \(90\) must be justified by correct method.[2 marks]
(i) 21.3 (A1)
(ii)
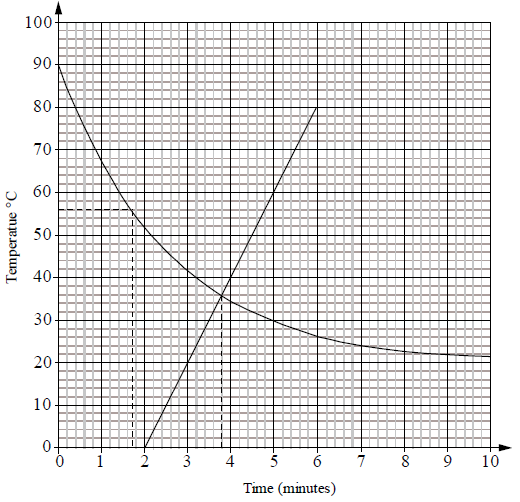(A4)(ft)
Note: Scales and labels (A1). Smooth curve (A1). All points correct including the \(y\)-intercept (A2), 1 point incorrect (A1), otherwise (A0). Follow through from their value of \(s\).
(iii) \(m = 1.7{\text{ minutes}}\) (Accept \( \pm 0.2\) ) (A2)(ft)
Note: Follow through from candidate’s graph. Accept answers in minutes and seconds if consistent with graph. If answer incorrect and correct line(s) seen on graph award (M1)(A0).
(iv) \({20^ \circ }{\text{C}}\) (A1)(ft)
The curve behaves asymptotically to the line \(y = 20\) or similar. (A1)
OR
The room temperature is 20 or similar
OR
When \({\text{m}}\) is a very large number the term \(70 \times {2.72^{ – 0.4{\text{m}}}}\) tends to zero or similar.
Note: Follow through from their graph if appropriate.[9 marks]
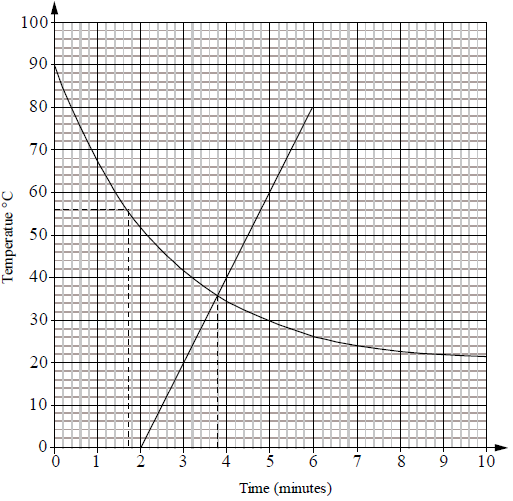(A1)(A1)
Notes: (A1) for correct line, (A1) for domain. If line not drawn on same set of axes award at most (A1)(A0).[2 marks]
It indicates by how much the temperature increases per minute. (A1)[1 mark]
(i) \(m = 3.8\) (Accept \( \pm 0.1\) ) (A2)(ft)
Note: Follow through from candidate’s graph. Accept answers in minutes and seconds if consistent with graph. If answer incorrect and correct line(s) seen on graph award (M1)(A0).
(ii) \(3.8 < m \leqslant 6\) (A1)(A1)(ft)
Note: (A1) for \(m > 3.8\) and (A1) for \(m \leqslant 6\). Follow through from candidate’s answer to part (e)(i). If candidate was already penalized in (c) for domain and does not state \(m \leqslant 6\) then award (A2)(ft).