Question
The function f is defined by \(f(x) = \frac{2}{x} + 3x^2 – 3, x \neq 0\).
(a) Find f'(x)
(b) Find the equation of the normal to the curve y = f(x) at (1, 2) in the form ax + by + d = 0, where \(a, b, d\epsilon \mathbb{Z}\).
Answer/Explanation
Ans:
(a) \(f'(x) = -2x^{-2}+6x\) OR \(f'(x) = -\frac{2}{x^2}+6x\)
(b) finding gradient at x = 1
\(\left.\begin{matrix}
\frac{dy}{dx}
\end{matrix}\right|_{x=1}=4\)
finding the perpendicular gradient
\(m_{\perp} = -\frac{1}{4}\)
\(2=-\frac{1}{4}(1)+c\) OR \(y-2 = -\frac{1}{4}(x-1)\)
x + 4y – 9 = 0
Question
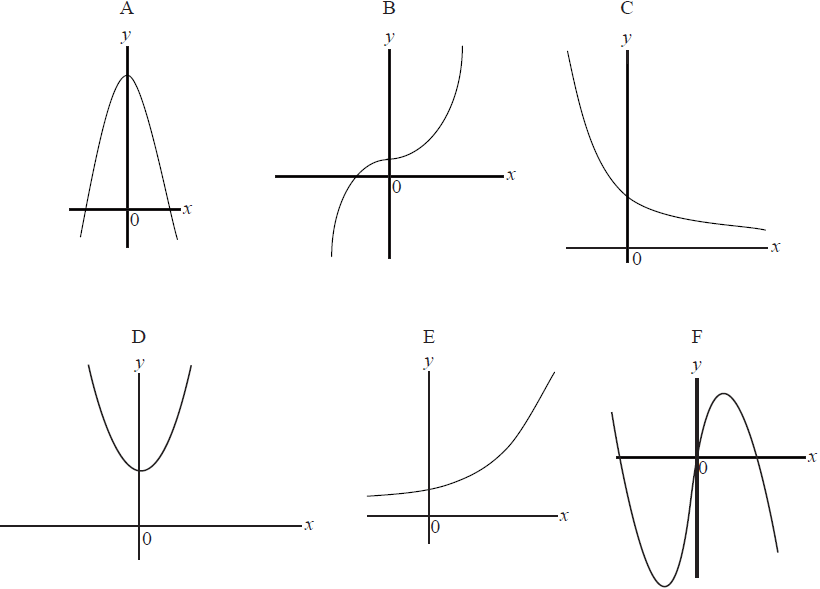
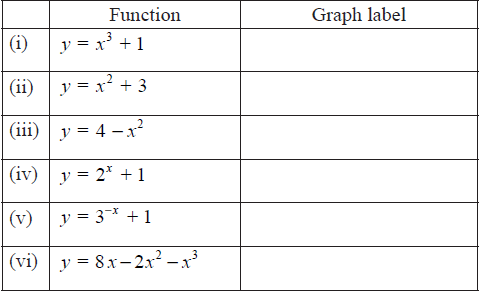
The following curves are sketches of the graphs of the functions given below, but in a different order. Using your graphic display calculator, match the equations to the curves, writing your answers in the table below.
(the diagrams are not to scale)
Answer/Explanation
Markscheme
(i) B (A1)
(ii) D (A1)
(iii) A (A1)
(iv) E (A1)
(v) C (A1)
(vi) F (A1) (C6)[6 marks]
Question
The straight line, L, has equation \(2y – 27x – 9 = 0\).
Find the gradient of L.[2]
Sarah wishes to draw the tangent to \(f (x) = x^4\) parallel to L.
Write down \(f ′(x)\).[1]
Find the x coordinate of the point at which the tangent must be drawn.[2]
Write down the value of \(f (x)\) at this point.[1]
Answer/Explanation
Markscheme
y = 13.5x + 4.5 (M1)
Note: Award (M1) for 13.5x seen.
gradient = 13.5 (A1) (C2)[2 marks]
4x3 (A1) (C1)[1 mark]
4x3 = 13.5 (M1)
Note: Award (M1) for equating their answers to (a) and (b).
x = 1.5 (A1)(ft)[2 marks]
\(\frac{{81}}{{16}}\) (5.0625, 5.06) (A1)(ft) (C3)
Note: Award (A1)(ft) for substitution of their (c)(i) into x4 with working seen.[1 mark]
Question
Consider the curve \(y = 1 + \frac{1}{{2x}},\,\,x \ne 0.\)
For this curve, write down
i) the value of the \(x\)-intercept;
ii) the equation of the vertical asymptote.[3]
Sketch the curve for \( – 2 \leqslant x \leqslant 4\) on the axes below.
 [3]
[3]
Answer/Explanation
Markscheme
i) \(\left( {x = } \right) – 0.5\,\,\left( { – \frac{1}{2}} \right)\) (A1)
ii) \(x = 0\) (A1)(A1) (C3)
Note: Award (A1) for “\(x = \)” and (A1) for “\(0\)” seen as part of an equation.
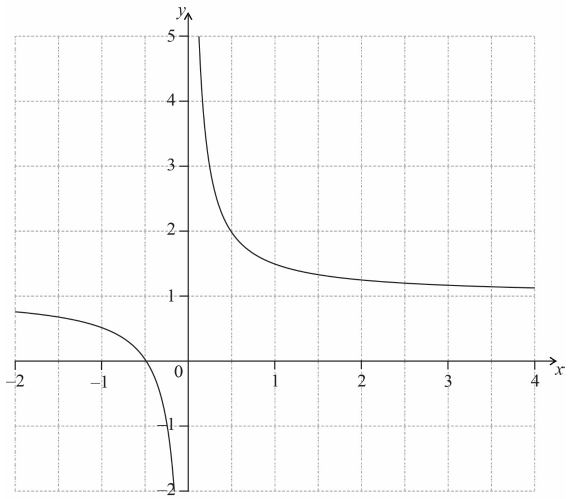
(A1)(ft)(A1)(ft)(A1) (C3)
Note: Award (A1)(ft) for correct \(x\)-intercept, (A1)(ft) for asymptotic behaviour at \(y\)-axis, (A1) for approximately correct shape (cannot intersect the horizontal asymptote of \(y = 1\)). Follow through from part (a).
