Question 1 [Maximum mark: 5]
The amount, in milligrams, of a medicinal drug in the body t hours after it was injected is given by D(t) = 23(0.85) t , t ≥ 0. Before this injection, the amount of the drug in the body was zero.
a.(i) Write down the initial dose of the drug.
(ii). the percentage of the drug that leaves the body each hour. [3]
c. Calculate the amount of the drug remaining in the body 10 hours after the injection. [2]
Answer/Explanation
(a) (i) 23 mg
(ii) \(1 0.85\) OR \(\frac{23-19.55}{23}\) OR \(0.15\)
\(15%\)
(b) \(23(0.85)^{10}\)
\(4.53 mg (4.52811…)\)
Question
A store sells bread and milk. On Tuesday, 8 loaves of bread and 5 litres of milk were sold for $21.40. On Thursday, 6 loaves of bread and 9 litres of milk were sold for $23.40.
If \(b =\) the price of a loaf of bread and \(m =\) the price of one litre of milk, Tuesday’s sales can be written as \(8b + 5m = 21.40\).
Using simplest terms, write an equation in b and m for Thursday’s sales.[2]
Find b and m.[2]
Draw a sketch, in the space provided, to show how the prices can be found graphically.
[2]
Answer/Explanation
Markscheme
Thursday’s sales, \(6b + 9m = 23.40\) (A1)
\(2b + 3m = 7.80\) (A1) (C2)[2 marks]
\(m = 1.40\) (accept 1.4) (A1)(ft)
\(b = 1.80\) (accept 1.8) (A1)(ft)
Award (A1)(d) for a reasonable attempt to solve by hand and answer incorrect. (C2)[2 marks]
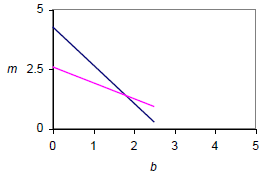(A1)(A1)(ft)
(A1) each for two reasonable straight lines. The intersection point must be approximately correct to earn both marks, otherwise penalise at least one line.
Note: The follow through mark is for candidate’s line from (a). (C2)[2 marks]
Question
A plumber in Australia charges 90 AUD per hour for work, plus a fixed cost. His total charge is represented by the cost function C = 60 + 90t, where t is in hours.
Write down the fixed cost.[1]
It takes \(3 \frac{1}{2}\) hours to complete a job for Paula. Find the total cost.[2]
Steve received a bill for 510 AUD. Calculate the time it took the plumber to complete the job.[3]
Answer/Explanation
Markscheme
AUD 60 (A1) (C1)[1 mark]
C = 60 + 90(3.5) = AUD 375 (M1)(A1) (C2)
Note: Award (M1) for correct substitution of 3.5.[2 marks]
Note: Unit penalty (UP) applies in this part
510 = 60 + 90t (M1)(A1)
(UP) t = 5h (hours, hrs) (A1) (C3)
Note: Award (M1) for setting formula = to any number.
(A1) for 510 seen.[3 marks]
Question
The function \(f(x) = 5 – 3({2^{ – x}})\) is defined for \(x \geqslant 0\).
On the axes below sketch the graph of f (x) and show the behaviour of the curve as x increases.[3]
Write down the coordinates of any intercepts with the axes.
[1]
Draw the line y = 5 on your sketch.[1]
Write down the number of solutions to the equation f (x) = 5 .[1]
Answer/Explanation
Markscheme
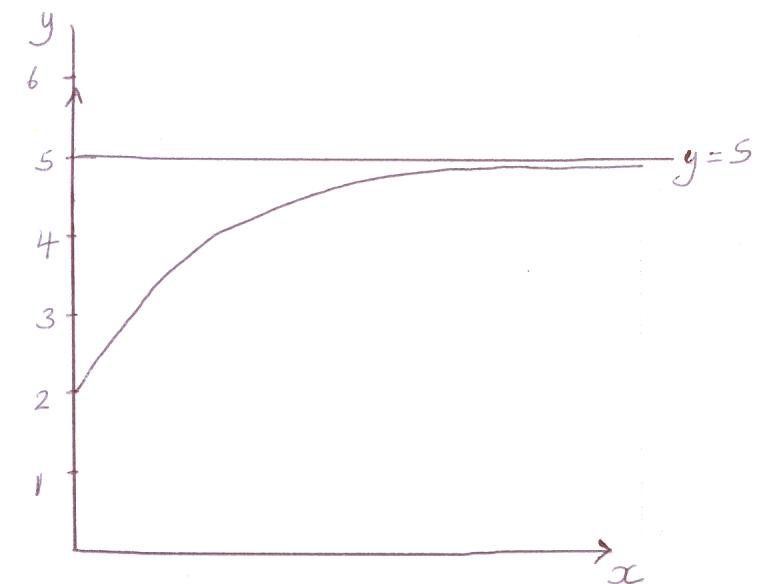(A1)(A1)(A1)
Notes: Award (A1) for labels and scale on y-axis.
Award (A1) for smooth increasing curve in the given domain.
Award (A1) for asymptote implied (\({\text{gradient}} \to {\text{0}}\)).
[3 marks]
(0, 2) accept x = 0, y = 2 (A1) (C4)
Note: If incorrect domain used and both (0, 2) and (\( – \)0.737, 0) seen award (A1)(ft).
[1 mark]
line passing through (0, 5), parallel to x axis and not intersecting their graph. (A1) (C1)
[1 mark]
zero (A1) (C1)
[1 mark]
Examiners report
Most candidates attempted this question and many gained 3 or 4 marks. All made an attempt at sketching the graph which demanded that students used their GDC. Many candidates failed to label their graphs and to give an indication of scale, and lost one mark in part (a). Some did not pay attention to the domain and sketched the graph in a different region. A significant number could also write down the coordinates of the y-intercept, although some wrote only y = 2 instead of giving the two coordinates. Almost all could draw the line y = 5 on the sketch but many could not find the answer for the number of solutions to the equation given in part c). Some candidates lost time in an attempt to draw this graph accurately on graph paper, which was not the intended task. Most candidates attempted this question, which clearly indicated that the time given for the paper was sufficient.
Most candidates attempted this question and many gained 3 or 4 marks. All made an attemptat sketching the graph which demanded that students used their GDC. Many candidates failed to label their graphs and to give an indication of scale, and lost one mark in part (a). Some did not pay attention to the domain and sketched the graph in a different region. A significant number could also write down the coordinates of the y-intercept, although some wrote onlyy = 2 instead of giving the two coordinates. Almost all could draw the line y = 5 on thesketch but many could not find the answer for the number of solutions to the equation given in part c). Some candidates lost time in an attempt to draw this graph accurately on graphpaper, which was not the intended task. Most candidates attempted this question, which clearly indicated that the time given for the paper was sufficient.
Most candidates attempted this question and many gained 3 or 4 marks. All made an attemptat sketching the graph which demanded that students used their GDC. Many candidates failed to label their graphs and to give an indication of scale, and lost one mark in part (a). Some did not pay attention to the domain and sketched the graph in a different region. A significant number could also write down the coordinates of the y-intercept, although some wrote onlyy = 2 instead of giving the two coordinates. Almost all could draw the line y = 5 on thesketch but many could not find the answer for the number of solutions to the equation given in part c). Some candidates lost time in an attempt to draw this graph accurately on graphpaper, which was not the intended task. Most candidates attempted this question, which clearly indicated that the time given for the paper was sufficient.
Most candidates attempted this question and many gained 3 or 4 marks. All made an attemptat sketching the graph which demanded that students used their GDC. Many candidates failed to label their graphs and to give an indication of scale, and lost one mark in part (a). Some did not pay attention to the domain and sketched the graph in a different region. A significant number could also write down the coordinates of the y-intercept, although some wrote onlyy = 2 instead of giving the two coordinates. Almost all could draw the line y = 5 on thesketch but many could not find the answer for the number of solutions to the equation given in part c). Some candidates lost time in an attempt to draw this graph accurately on graphpaper, which was not the intended task. Most candidates attempted this question, which clearly indicated that the time given for the paper was sufficient.
Question
Water has a lower boiling point at higher altitudes. The relationship between the boiling point of water (T) and the height above sea level (h) can be described by the model \(T = -0.0034h +100\) where T is measured in degrees Celsius (°C) and h is measured in metres from sea level.
Write down the boiling point of water at sea level.[1]
Use the model to calculate the boiling point of water at a height of 1.37 km above sea level.[3]
Water boils at the top of Mt. Everest at 70 °C.
Use the model to calculate the height above sea level of Mt. Everest.[2]
Answer/Explanation
Markscheme
100 °C (A1) (C1)[1 mark]
\(T = -0.0034 \times 1370 + 100\) (A1)(M1)
Note: Award (A1) for 1370 seen, (M1) for substitution of their h into the equation.
95.3 °C (95.342) (A1) (C3)
Notes: If their h is incorrect award at most (A0)(M1)(A0). If their h = 1.37 award at most (A0)(M1)(A1)(ft).[3 marks]
\(70 = -0.0034h + 100\) (M1)
Note: Award (M1) for correctly substituted equation.
h = 8820 m (8823.52…) (A1) (C2)
Note: The answer is 8820 m (or 8.82 km.) units are required.[2 marks]