Question
Ellis designs a gift box. The top of the gift box is in the shape of a right-angled triangle GIK. A rectangular section HIJL is inscribed inside this triangle. The lengths of GH, JK, HL,
and LJ are p cm, q cm, 8 cm and 6 cm respectively.
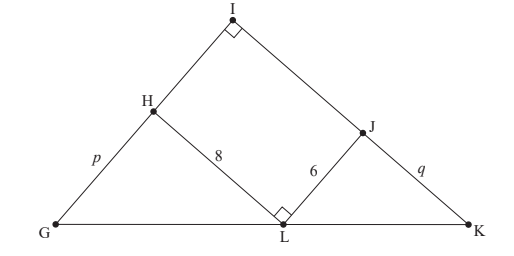
The area of the top of the gift box is A cm2.
a (i) Find A in terms of p and q .
(ii) Show that A = \(\frac{192}{q}\) + 3q + 48. [4]
(b) Find \(\frac{dA}{dq}\) [2]
Ellis wishes to find the value of q that will minimize the area of the top of the gift box.
(c) (i) Write down an equation Ellis could solve to find this value of q .
(ii) Hence, or otherwise, find this value of q . [2]
▶️Answer/Explanation
(a) (i) A = \(\frac{1}{2}\times6\times q + \frac{1}{2}\times8 \times p + 48\) OR A = \(\frac{1}{2}(p+6)(q+8)\) OR A = 3q+4q + 48 (ii) valid attempt to link p and q, using tangents, similar triangles or other method eg. tan Θ = \(\frac{8}{p}\) and tan Θ = \(\frac{q}{6}\) OR tan Θ = \(\frac{p}{8}\) tan Θ = \(\frac{6}{q}\) OR \(\frac{8}{9}= \frac{q}{6}\) correct equation linking p and q eg. p q = 48 OR p = \(\frac{48}{q}\) OR q = \(\frac{48}{p}\) substitute p = \(\frac{48}{q}\) into a correct area expression eg. (A =) \(\frac{1}{2}\times6\times q + \frac{1}{2}\times8 \times p + 48\) OR (A =) \(\frac{1}{2}(\frac{48}{q}+ 6)(q+8)\) A = 3q + 48 (b) \(\frac{-192}{q^{2}}+3\) (c) (i) \(\frac{-192}{q^{2}}+3\) = 0 (ii) q = 8 cm
Question
A triangular field ABC is such that AB = 56 m and BC = 82 m , each measured correct to the nearest metre, and the angle at B is equal to 105‘, measured correct to the nearest 5′.
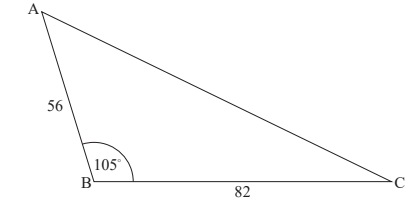
Calculate the maximum possible area of the field.
▶️Answer/Explanation
attempt to find any relevant maximum value largest sides are 56.5 and 82.5 smallest possible angle is 102.5 attempt to substitute into area of a triangle formula \(\frac{1}{2}\)×56.5× 82.5 × sin (102.5) = 2280m2 (2275.37…)
Question
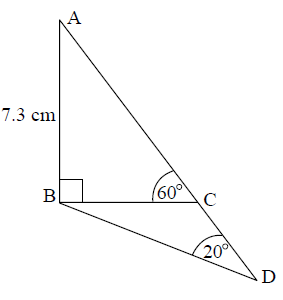
Triangle \({\text{ABC}}\) is drawn such that angle \({\text{ABC}}\) is \({90^ \circ }\), angle \({\text{ACB}}\) is \({60^ \circ }\) and \({\text{AB}}\) is \(7.3{\text{ cm}}\).
(i) Sketch a diagram to illustrate this information. Label the points \({\text{A, B, C}}\). Show the angles \({90^ \circ }\), \({60^ \circ }\) and the length \(7.3{\text{ cm}}\) on your diagram.
(ii) Find the length of \({\text{BC}}\).[3]
Point \({\text{D}}\) is on the straight line \({\text{AC}}\) extended and is such that angle \({\text{CDB}}\) is \({20^ \circ }\).
(i) Show the point \({\text{D}}\) and the angle \({20^ \circ }\) on your diagram.
(ii) Find the size of angle \({\text{CBD}}\).[3]
▶️Answer/Explanation
Markscheme
Unit penalty (UP) is applicable where indicated in the left hand column.
(i)
 (A1)
(A1)
For \({\text{A}}\), \({\text{B}}\), \({\text{C}}\), \(7.3\), \({60^ \circ }\), \({90^ \circ }\), shown in correct places (A1)
Note: The \({90^ \circ }\) should look like \({90^ \circ }\) (allow \( \pm {10^ \circ }\))
(ii) Using \(\tan 60\) or \(\tan 30\) (M1)
(UP) \(4.21{\text{ cm}}\) (A1)(ft)
Note: (ft) on their diagram
Or
Using sine rule with their correct values (M1)
(UP) \( = 4.21{\text{ cm}}\) (A1)(ft)
Or
Using special triangle \(\frac{{7.3}}{{\sqrt 3 }}\) (M1)
(UP) \(4.21{\text{ cm}}\) (A1)(ft)
Or
Any other valid solution
Note: If A and B are swapped then \({\text{BC}} = 8.43{\text{ cm}}\) (C3)[3 marks]
(i) For \({\text{ACD}}\) in a straight line and all joined up to \({\text{B}}\), for \({20^ \circ }\) shown in correct place and \({\text{D}}\) labelled. \({\text{D}}\) must be on \({\text{AC}}\) extended. (A1)
(ii) \({\text{B}}\hat {\text{C}}{\text{D}} = {120^ \circ }\) (A1)
\({\text{C}}\hat {\text{B}}{\text{D}} = {40^ \circ }\) (A1) (C3)[3 marks]
Question
A and B are points on a straight line as shown on the graph below.
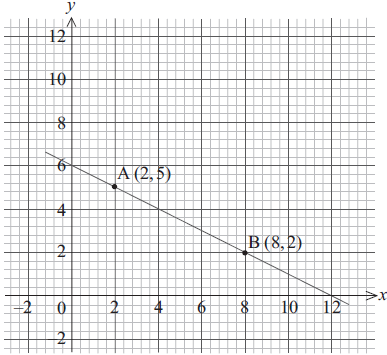
Write down the y-intercept of the line AB.[1]
Calculate the gradient of the line AB.[2]
The acute angle between the line AB and the x-axis is θ.
Show θ on the diagram.[1]
The acute angle between the line AB and the x-axis is θ.
Calculate the size of θ.[2]
▶️Answer/Explanation
Markscheme
6
OR
(0, 6) (A1) (C1)[1 mark]
\(\frac{{(2 – 5)}}{{(8 – 2)}}\) (M1)
Note: Award (M1) for substitution in gradient formula.
\( = – \frac{1}{2}\) (A1) (C2)[2 marks]
Angle clearly identified. (A1) (C1)[1 mark]
\(\tan \theta = \frac{1}{2}\) (or equivalent fraction) (M1)
\(\theta = 26.6^\circ\) (A1)(ft) (C2)
Note: (ft) from (b).
Accept alternative correct trigonometrical methods.[2 marks]
Question
José stands 1.38 kilometres from a vertical cliff.
Express this distance in metres.[1]
José estimates the angle between the horizontal and the top of the cliff as 28.3° and uses it to find the height of the cliff.
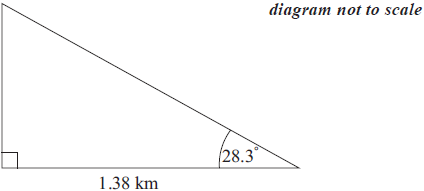
Find the height of the cliff according to José’s calculation. Express your answer in metres, to the nearest whole metre.[3]
José estimates the angle between the horizontal and the top of the cliff as 28.3° and uses it to find the height of the cliff.
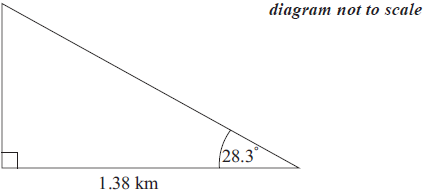
The actual height of the cliff is 718 metres. Calculate the percentage error made by José when calculating the height of the cliff.[2]
▶️Answer/Explanation
Markscheme
1380 (m) (A1) (C1)[1 mark]
\(1380\tan 28.3\) (M1)
\( = 743.05 \ldots \) . (A1)(ft)
\( = 743\) (m) (A1)(ft) (C3)
Notes: Award (M1) for correct substitution in tan formula or equivalent, (A1)(ft) for their 743.05 seen, (A1)(ft) for their answer correct to the nearest m.[3 marks]
\({\text{percentage error}} = \frac{{743.05 \ldots – 718}}{{718}} \times 100\) (M1)
Note: Award (M1) for correct substitution in formula.
= 3.49 % (% symbol not required) (A1)(ft) (C2)
Notes: Accept 3.48 % for use of 743.
Accept negative answer.[2 marks]
