Question 9. [Maximum mark: 7]
A garden includes a small lawn. The lawn is enclosed by an arc AB of a circle with centre O and radius 6 m, such that AÔB = 135° . The straight border of the lawn is defined by chord [AB].The lawn is shown as the shaded region in the following diagram.
diagram not to scale
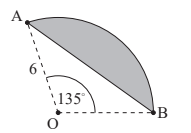
a. A footpath is to be laid around the curved side of the lawn. Find the length of the footpath. [3]
b. Find the area of the lawn. [4]
Answer/Explanation
(a) 135° \(\times \frac{12\pi }{360°}14.1(m)(14.1271..)\)
(b) evidence of splitting region into two areas \(135° \times \frac{\pi 6}{360°}-\frac{6\times 6\times sin135^{\circ}}{2} \rightarrow 42.4115 ..− 12.7279 ….=29.7 m^{2}\)
Question 12. [Maximum mark: 8]
Ellis designs a gift box. The top of the gift box is in the shape of a right-angled triangle GIK. A rectangular section HIJL is inscribed inside this triangle. The lengths of GH, JK, HL,
and LJ are p cm, q cm, 8 cm and 6 cm respectively.
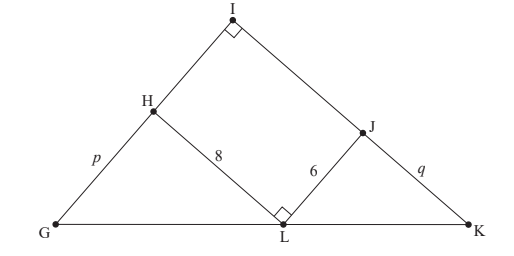
The area of the top of the gift box is A cm2.
a (i) Find A in terms of p and q .
(ii) Show that A = \(\frac{192}{q}\) + 3q + 48. [4]
(b) Find \(\frac{dA}{dq}\) [2]
Ellis wishes to find the value of q that will minimize the area of the top of the gift box.
(c) (i) Write down an equation Ellis could solve to find this value of q .
(ii) Hence, or otherwise, find this value of q . [2]
Answer/Explanation
(a) (i) A = \(\frac{1}{2}\times6\times q + \frac{1}{2}\times8 \times p + 48\) OR
\(A = \frac{1}{2}(p+6)(q+8)\) OR \(A = 3q+4q + 48\)
(ii) valid attempt to link p and q, using tangents, similar triangles or other method eg.
\(tan Θ = \frac{8}{p}\) and
\(tan Θ = \frac{q}{6}\) OR
\(tan Θ = \frac{p}{8}\)
\(tan Θ = \frac{6}{q}\) OR \(\frac{8}{9} = \frac{q}{6}\) correct equation linking p and q eg. p q = 48 OR
\(p = \frac{48}{q}\) OR
\(q = \frac{48}{p}\) substitute \(p = \frac{48}{q}\)
into a correct area expression
\(A = \frac{1}{2}\times6\times q + \frac{1}{2}\times8 \times p + 48\) OR
\(A = \frac{1}{2}(\frac{48}{q}+ 6)(q+8)\)
\(A = 3q + 48\)
(b) \(\frac{-192}{q^{2}}+3\) (c) (i) \(\frac{-192}{q^{2}}+3\) = 0
(ii) q = 8 cm
Question 9. [Maximum mark: 5]
A triangular field ABC is such that AB = 56 m and BC = 82 m , each measured correct to the nearest metre, and the angle at B is equal to 105‘, measured correct to the nearest 5′.
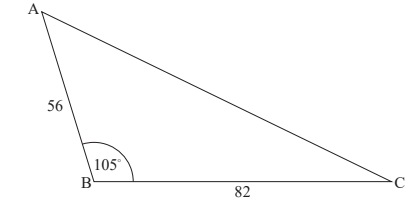
Calculate the maximum possible area of the field.
Answer/Explanation
largest sides are 56.5 and 82.5 smallest possible angle is 102.5 substitute into area of a triangle formula
\(\frac{1}{2}\times 56.5\times 82.5 \times sin (102.5) = 2280 m^{2} \rightarrow (2275.37…)\)
Question
Question
The front view of a doghouse is made up of a square with an isosceles triangle on top.
The doghouse is 1.35 m high and 0.9m wide, and sits on a square base.
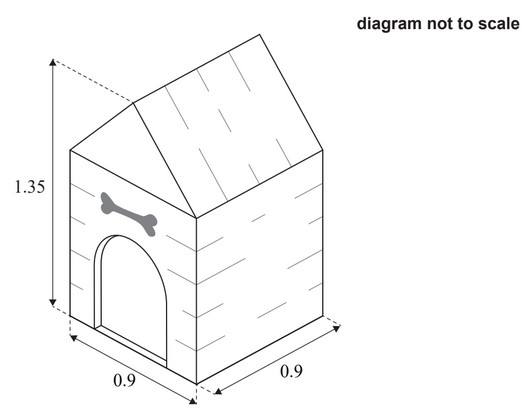
The top of the rectangular surfaces of the roof of the doghouse are to be painted
Find the area to be painted.
Answer/Explanation
Ans:
height of triangle at roof = 1.35 – 0.9 = 0.45
slant height = \(\sqrt{0.45^2 + 0.45^2}\) OR \(sin(45^o)=\frac{0.45}{slant height}\)
\(=\sqrt{0.405}(0.636396…, 0.45 \sqrt{2}\)
area of one rectangle on roof = \(\sqrt{0.405} \times 0.9 (=0.572756…)\)
area painted = \((2 \times \sqrt{0.405} \times 0.9 = 2 \times 0.572756…)\)
1.15 \(m^2\) (1.14551… \(m^2\), 0.81 \(\sqrt{2} m^2 \))
Question
Triangle \({\text{ABC}}\) is drawn such that angle \({\text{ABC}}\) is \({90^ \circ }\), angle \({\text{ACB}}\) is \({60^ \circ }\) and \({\text{AB}}\) is \(7.3{\text{ cm}}\).
(i) Sketch a diagram to illustrate this information. Label the points \({\text{A, B, C}}\). Show the angles \({90^ \circ }\), \({60^ \circ }\) and the length \(7.3{\text{ cm}}\) on your diagram.
(ii) Find the length of \({\text{BC}}\).[3]
Point \({\text{D}}\) is on the straight line \({\text{AC}}\) extended and is such that angle \({\text{CDB}}\) is \({20^ \circ }\).
(i) Show the point \({\text{D}}\) and the angle \({20^ \circ }\) on your diagram.
(ii) Find the size of angle \({\text{CBD}}\).[3]
Answer/Explanation
Markscheme
Unit penalty (UP) is applicable where indicated in the left hand column.
(i)
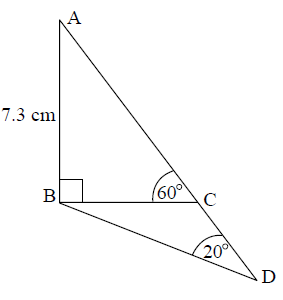 (A1)
(A1)
For \({\text{A}}\), \({\text{B}}\), \({\text{C}}\), \(7.3\), \({60^ \circ }\), \({90^ \circ }\), shown in correct places (A1)
Note: The \({90^ \circ }\) should look like \({90^ \circ }\) (allow \( \pm {10^ \circ }\))
(ii) Using \(\tan 60\) or \(\tan 30\) (M1)
(UP) \(4.21{\text{ cm}}\) (A1)(ft)
Note: (ft) on their diagram
Or
Using sine rule with their correct values (M1)
(UP) \( = 4.21{\text{ cm}}\) (A1)(ft)
Or
Using special triangle \(\frac{{7.3}}{{\sqrt 3 }}\) (M1)
(UP) \(4.21{\text{ cm}}\) (A1)(ft)
Or
Any other valid solution
Note: If A and B are swapped then \({\text{BC}} = 8.43{\text{ cm}}\) (C3)[3 marks]
(i) For \({\text{ACD}}\) in a straight line and all joined up to \({\text{B}}\), for \({20^ \circ }\) shown in correct place and \({\text{D}}\) labelled. \({\text{D}}\) must be on \({\text{AC}}\) extended. (A1)
(ii) \({\text{B}}\hat {\text{C}}{\text{D}} = {120^ \circ }\) (A1)
\({\text{C}}\hat {\text{B}}{\text{D}} = {40^ \circ }\) (A1) (C3)[3 marks]
