Question 4 [Maximum mark: 6]
The diagram below shows a helicopter hovering at point H, 380 m vertically above a lake. Point A is the point on the surface of the lake, directly below the helicopter.
diagram not to scale
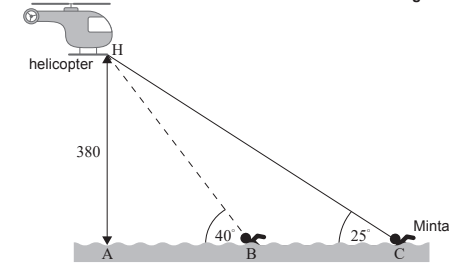
Minta is swimming at a constant speed in the direction of point A. Minta observes the helicopter from point C as she looks upward at an angle of 25°. After 15 minutes, Minta is at point B and she observes the same helicopter at an angle of 40°.
Find the distance from A to C. [2]
Find the distance from B to C. [3]
Find Minta’s speed, in metres per hour. [1]
Answer/Explanation
(a) AC= \(\frac{380}{tan25°}\) OR \(AC= \sqrt{\frac{380}{sin25°}-380^{2}}\) OR
\(\frac{380}{tan25°}=\frac{AC}{sin65°}\)\)
\(AC = 815 M (814.912…)\)
(b) AB = \(\frac{280}{tan40°}\)
= 453m (452.866..)
BC= 814.912…-452.866..
METHOD 2 attempt to find HB
\(HB =\frac{380}{sin40}\rightarrow
591m (=591.175…) \)
\(BC = \frac{591.175…\times sin15°}{sin25°}\)
\(= 362m (362.0.46..)\)
(c) \(362.046..\times 4 = 1450mh(1448.18..)\)
Question 9. [Maximum mark: 5]
A triangular field ABC is such that AB = 56 m and BC = 82 m , each measured correct to the nearest metre, and the angle at B is equal to 105‘, measured correct to the nearest 5′.
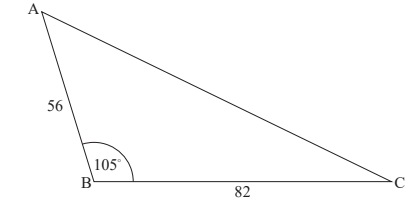
Calculate the maximum possible area of the field.
Answer/Explanation
largest sides are 56.5 and 82.5 smallest possible angle is 102.5 substitute into area of a triangle formula
\(\frac{1}{2}\times 56.5\times 82.5 \times sin (102.5) = 2280 m^{2} \rightarrow (2275.37…)\)
Question
The height of a baseball after it is hit by a bat is modelled by the function
\(h(t) = -4.8t^2 + 21t + 1.2\)
where h(t) is the height in metres above the ground and t is the time in seconds after the ball was hit.
(a) Write down the height of the ball above the ground at the instant it is hit by the bat.
(b) Find the value of t when the ball hits the ground.
(c) State an appropriate domain for t in this model.
Answer/Explanation
Ans:
(a) 1.2 metres
(b) \(-4.8t^2 + 21t + 1.2 = 0\)
(t=) 4.43s (4.431415…s)
(c) \(0 \leq t \leq 4.43\) OR [0, 4.43]
Question
A vertical pole stands on horizontal ground. The bottom of the pole is taken as the origin, O
of a coordinate system in which the top, F, of the pole has coordinates (0, 0, 5.8). All units
are in metres.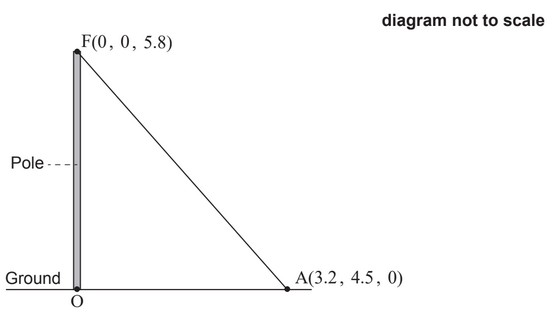
The pole is held in place by ropes attached at F.
One of the ropes is attached to the ground at a point A with coordinates (3.2, 4.5, 0).
The rope forms a straight line from A to F.
(a) Find the length of the rope connecting A to F.
(b) Find \(F \widehat{A} O\), the angle the rope makes with the ground.
Answer/Explanation
Ans:
(a) \(\sqrt{3.2^2 + 4.5^2 +5.8^2}\)
=8.01 (8.00812…) m
(b) \(F\widehat{A} O = sin^{-1} (\frac{5.8}{8.00812…})\) OR \(cos^{-1}(\frac{5.52177…}{8.00812…})\) OR \(tan^{-1}(\frac{5.8}{5.52177…})\)
\(46.4^o (46.4077…^o)\)
