Question
. The diagram shows a sector, OAB, of a circle with centre O and radius r,
such that AÔB = θ.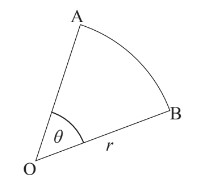
Sam measured the value of r to be 2 cm and the value of θ to be \(30^∘\).
(a) Use Sam’s measurements to calculate the area of the sector. Give your answer to
four significant figures.
It is found that Sam’s measurements are accurate to only one significant figure.
(b) Find the upper bound and lower bound of the area of the sector.
(c) Find, with justification, the largest possible percentage error if the answer to part (a)
is recorded as the area of the sector.
▶️Answer/Explanation
Ans:
(a) \(\pi \times 2^2 \times \frac{30}{360}\)
= 1.047 \(cm^2\)
(b) attempt to substitute any two values from 1.5, 2.5, 25 or 35 into area of sector formula
(upper bound = \(\pi \times 2.5^2 \times \frac{35}{360}=)\) 1.91 \(cm^2\) (1.90895….)
(lower bound = \(\pi \times 1.5^2 \times \frac{25}{360}=)\) 0.491 \(cm^2\) (0.490873…)
(c) \((\begin{vmatrix}
\frac{1.047-0.490873…}{0.490873…}
\end{vmatrix} \times 100=) 45.2 (%) (45.1532…)\)
\((\begin{vmatrix}
\frac{1.047-0.490873…}{0.490873…}
\end{vmatrix} \times 100=)113 (%) (113.293…)\)
so the largest percentage error is 113 %
Question
In the triangle ABC , AB = 8 , BC = 12 and AC = 10 . A circle is inscribed in this triangle.
(a) Find the lengths of the tangents from A, B and C to this inscribed circle. [3]
(b) (i) Show that the area of the triangle ABC is 15r , where r denotes the radius of the inscribed circle.
(ii) Show that \(sin \hat{A} = \frac{3\sqrt{7}}{8}\) .
(iii) Using parts (b) (i) and (ii), or otherwise, show that r is equal to , \(\sqrt{N}\) where N is a positive integer whose value is to be determined. [8]
▶️Answer/Explanation
Ans:
(a)
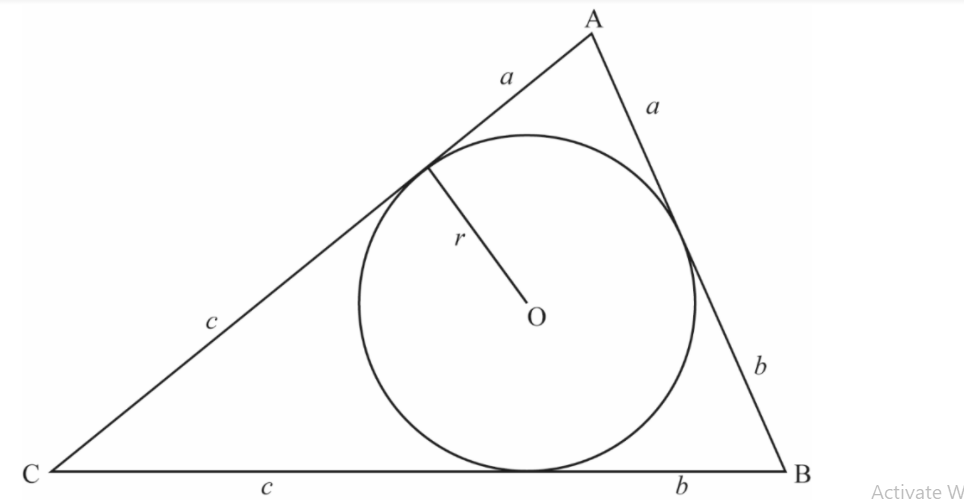
let the lengths of the tangents from A,B,C be a,b,c respectively. Then
b + c = 12, c + a = 10, a + b = 8
the solution is a = 3, b = 5, c = 7
(b)
(i) area of triangle = 3r + 5r+ 7r =15r
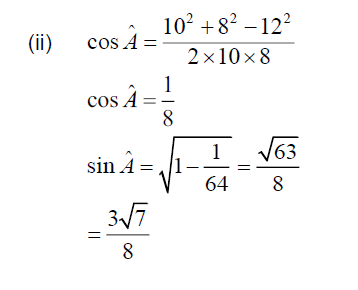
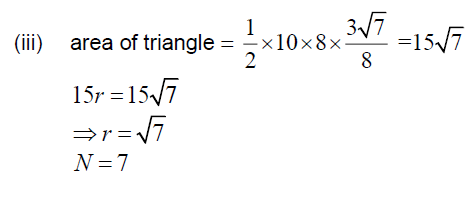
Question
Two line segments [\(\rm{AB}\)] and [\(\rm{CD}\)] meet internally at the point \(\rm{Y}\). Given that
a.\({\text{YA}} \times {\text{YB}} = {\text{YC}} \times {\text{YD }}\) show that \(\rm{A}\), \(\rm{B}\), \(\rm{C}\) and \(\rm{D}\) all lie on the circumference of a circle.[6]
b.Explain why the result also holds if the line segments meet externally at \(\rm{Y}\).[3]
▶️Answer/Explanation
Markscheme
METHOD 1
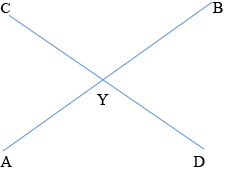
Consider the triangles \(\rm{ACY}\) and \(\rm{DBY}\) M1
Then \({\text{YA}} \times {\text{YB}} = {\text{YC}} \times {\text{YD }}\)
It follows that \(\frac{{{\text{YA}}}}{{{\text{YD}}}} = \frac{{{\text{YC}}}}{{{\text{YB}}}}\) A1
Also \({\rm{A\hat YC}} = {\rm{D\hat YB}}\) A1
The triangles \(\rm{ACY}\) and \(\rm{DBY}\) are therefore similar A1
So \({\rm{A\hat CY}} = {\rm{D\hat BY}}\) A1
Therefore by the converse to the angles subtended by a chord theorem,
the points \(\rm{A}\), \(\rm{B}\), \(\rm{C}\), \(\rm{D}\) lie on a circle. R1
METHOD 2
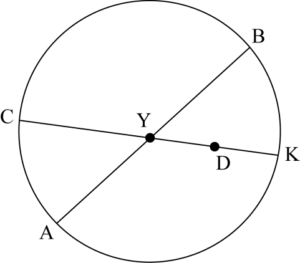
consider the circle passing through \(\rm{ABC}\) M1
the circle then cuts the line \((\rm{CD})\) at \(\rm{K}\) M1
Note: May be seen on diagram
since \(\rm{Y}\) lies inside the circle, \(\rm{Y}\) divides the chord \(\rm{CK}\) internally
hence \(\rm{K}\) and \(\rm{D}\) are on the same side of \(\rm{Y}\) (R1)
\({\text{YA}} \times {\text{YB}} = {\text{YC}} \times {\text{YK}}\) since \(\rm{A}\), \(\rm{B}\), \(\rm{C}\) and \(\rm{K}\) are concyclic M1
\({\text{YA}} \times {\text{YB}} = {\text{YC}} \times {\text{YD }}\) given
\( \Rightarrow {\text{YC}} \times {\text{YK}} = {\text{YC}} \times {\text{YD }}\) A1
hence \(\rm{K}\) and \(\rm{D}\) are the same point R1
the circle passes through \(\rm{D}\)
Note: Allow an argument based on similar triangles and angles in the segment
Do not allow the use of the converse of the intersecting chords theorem in either (a) or (b)
METHOD 1
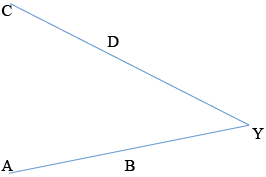
Since the triangles \(\rm{ACY}\) and \(\rm{DBY}\) are still similar \({\rm{A\hat CY}} = {\rm{D\hat BY}}\) A1
Therefore \({\rm{A\hat CY}} + {\rm{D\hat BA}} = {\rm{A\hat CY}} + 180^\circ – {\rm{D\hat BY}}\)
\( = 180^\circ \) A1
\(\rm{ACDB}\) is therefore a cyclic quadrilateral so the points \(\rm{A}\), \(\rm{B}\), \(\rm{C}\), \(\rm{D}\) lie on a circle. R1
METHOD 2
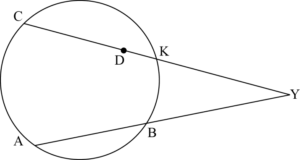
again consider the circle passing through \(\rm{ABC}\) and again let it cut the line \(\rm{CD}\) at \(\rm{K}\). M1
in this case \(\rm{Y}\) lies outside the circle \(\rm{ABC}\) and therefore \(\rm{Y}\) divides the chord \(\rm{CK}\) externally. M1
by the secant-secant theorem the same working applies as in part (a) R1
and the proof follows identically. AG
Question
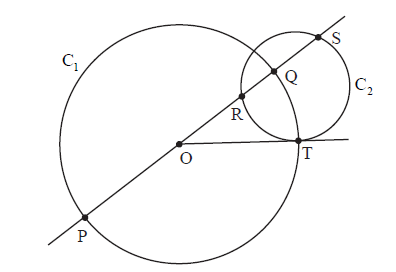
The figure shows a circle C1 with centre O and diameter [PQ] and a circle C2 which intersects (PQ) at the points R and S. T is one point of intersection of the two circles and (OT) is a tangent to C2 .
a.Show that \(\frac{{{\rm{OR}}}}{{{\rm{OT}}}} = \frac{{{\rm{OT}}}}{{{\rm{OS}}}}\) .[2]
b.(i) Show that \({\rm{PR}} – {\rm{RQ}} = 2{\rm{OR}}\) .
(ii) Show that \(\frac{{{\rm{PR}} – {\rm{RQ}}}}{{{\rm{PR}} + {\rm{RQ}}}} = \frac{{{\rm{PS}} – {\rm{SQ}}}}{{{\rm{PS}} + {\rm{SQ}}}}\) .[6]
▶️Answer/Explanation
Markscheme
by the tangent – secant theorem, M1
\({\rm{O}}{{\rm{T}}^2} = {\rm{OR}} \bullet {\rm{OS}}\) A1
so that \(\frac{{{\rm{OR}}}}{{{\rm{OT}}}} = \frac{{{\rm{OT}}}}{{{\rm{OS}}}}\) AG
[2 marks]
(i) \({\rm{PR}} – {\rm{RQ}} = {\rm{PO}} + {\rm{OR}} – ({\rm{OQ}} – {\rm{OR}})\) A1
\( = 2{\rm{OR}}\) AG
(ii) attempt to continue the process set up in (b)(i) (M1)
\({\rm{PR + RQ}} = {\rm{PO}} + {\rm{OR + OQ}} – {\rm{OR}} = 2{\rm{OT}}\) A1
\({\rm{PS}} – {\rm{SQ}} = {\rm{PQ}} + {\rm{QS}} – {\rm{SQ}} = 2{\rm{OT}}\) A1
\({\rm{PS + SQ}} = {\rm{PO}} + {\rm{OS}} – {\rm{OQ}} = 2{\rm{OS}}\) A1
it now follows that
\(\frac{{{\rm{PR}} – {\rm{RQ}}}}{{{\rm{PR}} + {\rm{RQ}}}} = \frac{{{\rm{OR}}}}{{{\rm{OT}}}}\) and \(\frac{{{\rm{PS}} – {\rm{SQ}}}}{{{\rm{PS}} + {\rm{SQ}}}} = \frac{{{\rm{OT}}}}{{{\rm{OS}}}}\) so using the result in part (a) R1
\(\frac{{{\rm{PR}} – {\rm{RQ}}}}{{{\rm{PR}} + {\rm{RQ}}}} = \frac{{{\rm{PS}} – {\rm{SQ}}}}{{{\rm{PS}} + {\rm{SQ}}}}\) AG
[6 marks]
Question
The triangle ABC is isosceles and AB = BC = 5. D is the midpoint of AC and BD = 4.
Find the lengths of the tangents from A, B and D to the circle inscribed in the triangle ABD.
▶️Answer/Explanation
Markscheme
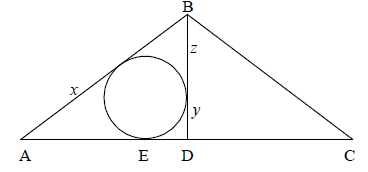
AD \( = 3\) (A1)
Let the lengths of the tangents be as shown.
Then,
\(x + y = 3\)
\(y + z = 4\)
\(x + z = 5\) (M1)A1
Solving,
\(x = 2\) , \(y = 1\) , \(z = 3\) A1A1A1
[6 marks]
