Question 1 [Maximum mark: 7]
Two schools are represented by points A(2, 20) and B(14 , 24) on the graph below. A road, represented by the line R with equation −x + y = 4 , passes near the schools. An architect is asked to determine the location of a new bus stop on the road such that it is the same distance from the two schools.
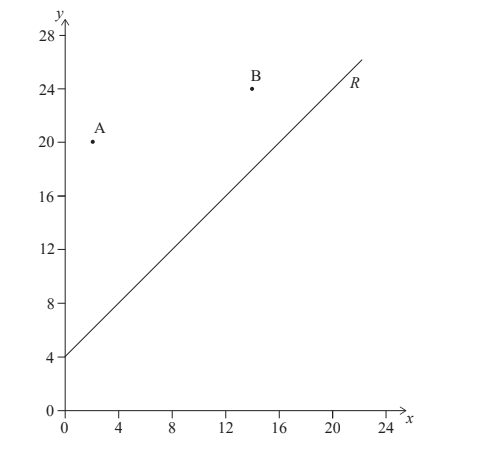
a. Find the equation of the perpendicular bisector of [AB] .Give your equation in the form y= mx + c . [5]
b. Determine the coordinates of the point on R where the bus stop should be located. [2]
▶️Answer/Explanation
(a) gradient \( AB = \frac{4}{12}(\frac{1}{3})\)
midpoint AB : (8, 22)
gradient of bisector \(= – \frac{1}{gradient AB}= -3 \)
perpendicular bisector: \(22 = -3 × 8+b\) OR
\((Y-22)= -3(X-8)\) perpendicular bisector: \(Y = -3x+ 46\)
(b) attempt to solve simultaneous equations \(x+ 4 = -3x+46\)
\(x=10.5,14.5\)
Question
The diagram below shows the graph of a line \(L\) passing through (1, 1) and (2 , 3) and the graph \(P\) of the function \(f (x) = x^2 − 3x − 4\)
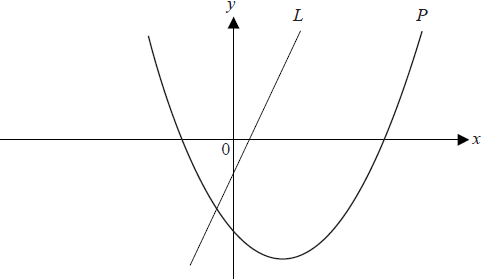
a.Find the gradient of the line L.[2]
b.Differentiate \(f (x)\) .[2]
c.Find the coordinates of the point where the tangent to P is parallel to the line L.[3]
d.Find the coordinates of the point where the tangent to P is perpendicular to the line L.[4]
e.Find
(i) the gradient of the tangent to P at the point with coordinates (2, − 6).
(ii) the equation of the tangent to P at this point.[3]
f.State the equation of the axis of symmetry of P.[1]
g.Find the coordinates of the vertex of P and state the gradient of the curve at this point.[3]
▶️Answer/Explanation
Markscheme
for attempt at substituted \(\frac{{ydistance}}{{xdistance}}\) (M1)
gradient = 2 (A1)(G2)[2 marks]
\(2x – 3\) (A1)(A1)
(A1) for \(2x\) , (A1) for \(-3\)[2 marks]
for their \(2x – 3 =\) their gradient and attempt to solve (M1)
\(x = 2.5\) (A1)(ft)
\(y = -5.25\) ((ft) from their x value) (A1)(ft)(G2)[3 marks]
for seeing \(\frac{{ – 1}}{{their(a)}}\) (M1)
solving \(2x – 3 = – \frac{1}{2}\) (or their value) (M1)
x = 1.25 (A1)(ft)(G1)
y = – 6.1875 (A1)(ft)(G1)[4 marks]
(i) \(2 \times 2 – 3 = 1\) ((ft) from (b)) (A1)(ft)(G1)
(ii) \(y = mx + c\) or equivalent method to find \(c \Rightarrow -6 = 2 + c\) (M1)
\(y = x – 8\) (A1)(ft)(G2)[3 marks]
\(x = 1.5\) (A1)[1 mark]
for substituting their answer to part (f) into the equation of the parabola (1.5, −6.25) accept x = 1.5, y = −6.25 (M1)(A1)(ft)(G2)
gradient is zero (accept \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\)) (A1)[3 marks]
Question
The diagram below shows the graph of a line \(L\) passing through (1, 1) and (2 , 3) and the graph \(P\) of the function \(f (x) = x^2 − 3x − 4\)
a.Find the gradient of the line L.[2]
b.Differentiate \(f (x)\) .[2]
c.Find the coordinates of the point where the tangent to P is parallel to the line L.[3]
d.Find the coordinates of the point where the tangent to P is perpendicular to the line L.[4]
e.Find
(i) the gradient of the tangent to P at the point with coordinates (2, − 6).
(ii) the equation of the tangent to P at this point.[3]
f.State the equation of the axis of symmetry of P.[1]
g.Find the coordinates of the vertex of P and state the gradient of the curve at this point.[3]
▶️Answer/Explanation
Markscheme
for attempt at substituted \(\frac{{ydistance}}{{xdistance}}\) (M1)
gradient = 2 (A1)(G2)[2 marks]
\(2x – 3\) (A1)(A1)
(A1) for \(2x\) , (A1) for \(-3\)[2 marks]
for their \(2x – 3 =\) their gradient and attempt to solve (M1)
\(x = 2.5\) (A1)(ft)
\(y = -5.25\) ((ft) from their x value) (A1)(ft)(G2)[3 marks]
for seeing \(\frac{{ – 1}}{{their(a)}}\) (M1)
solving \(2x – 3 = – \frac{1}{2}\) (or their value) (M1)
x = 1.25 (A1)(ft)(G1)
y = – 6.1875 (A1)(ft)(G1)[4 marks]
(i) \(2 \times 2 – 3 = 1\) ((ft) from (b)) (A1)(ft)(G1)
(ii) \(y = mx + c\) or equivalent method to find \(c \Rightarrow -6 = 2 + c\) (M1)
\(y = x – 8\) (A1)(ft)(G2)[3 marks]
\(x = 1.5\) (A1)[1 mark]
for substituting their answer to part (f) into the equation of the parabola (1.5, −6.25) accept x = 1.5, y = −6.25 (M1)(A1)(ft)(G2)
gradient is zero (accept \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\)) (A1)[3 marks]
Question
Consider the functions \(f(x) = \frac{{2x + 3}}{{x + 4}}\) and \(g(x) = x + 0.5\) .
a.Sketch the graph of the function \(f(x)\), for \( – 10 \leqslant x \leqslant 10\) . Indicating clearly the axis intercepts and any asymptotes.[6]
b.Write down the equation of the vertical asymptote.[2]
c.On the same diagram as part (a) sketch the graph of \(g(x) = x + 0.5\) .[2]
d.Using your graphical display calculator write down the coordinates of one of the points of intersection on the graphs of \(f\) and \(g\), giving your answer correct to five decimal places.[3]
e.Write down the gradient of the line \(g(x) = x + 0.5\) .[1]
f.The line \(L\) passes through the point with coordinates \(( – 2{\text{, }} – 3)\) and is perpendicular to the line \(g(x)\) . Find the equation of \(L\).[3]
▶️Answer/Explanation
Markscheme
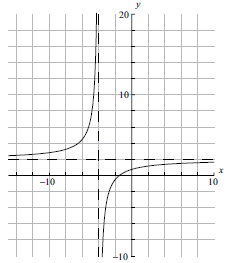(A6)
Notes: (A1) for labels and some idea of scale.
(A1) for \(x\)-intercept seen, (A1) for \(y\)-intercept seen in roughly the correct places (coordinates not required).
(A1) for vertical asymptote seen, (A1) for horizontal asymptote seen in roughly the correct places (equations of the lines not required).
(A1) for correct general shape.[6 marks]
\(x = – 4\) (A1)(A1)(ft)
Note: (A1) for \(x =\), (A1)(ft) for \( – 4\).[2 marks]
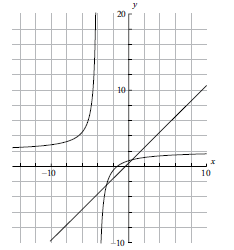(A1)(A1)
Note: (A1) for correct axis intercepts, (A1) for straight line[2 marks]
\(( – 2.85078{\text{, }} – 2.35078)\) OR \((0.35078{\text{, }}0.85078)\) (G1)(G1)(A1)(ft)
Notes: (A1) for \(x\)-coordinate, (A1) for \(y\)-coordinate, (A1)(ft) for correct accuracy. Brackets required. If brackets not used award (G1)(G0)(A1)(ft).
Accept \(x = – 2.85078\), \(y = – 2.35078\) or \(x = 0.35078\), \(y = 0.85078\).[3 marks]
\({\text{gradient}} = 1\) (A1)[1 mark]
\({\text{gradient of perpendicular}} = – 1\) (A1)(ft)
(can be implied in the next step)
\(y = mx + c\)
\( – 3 = – 1 \times – 2 + c\) (M1)
\(c = – 5\)
\(y = – x – 5\) (A1)(ft)(G2)
OR
\(y + 3 = – (x + 2)\) (M1)(A1)(ft)(G2)
Note: Award (G2) for correct answer with no working at all but (A1)(G1) if the gradient is mentioned as \( – 1\) then correct answer with no further working.[3 marks]
Question
a.On the coordinate axes below, \({\text{D}}\) is a point on the \(y\)-axis and \({\text{E}}\) is a point on the \(x\)-axis. \({\text{O}}\) is the origin. The equation of the line \({\text{DE}}\) is \(y + \frac{1}{2}x = 4\).
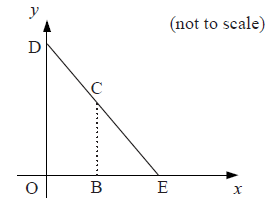
b.Write down the coordinates of point \({\text{E}}\).[2]
\({\text{C}}\) is a point on the line \({\text{DE}}\). \({\text{B}}\) is a point on the \(x\)-axis such that \({\text{BC}}\) is parallel to the \(y\)-axis. The \(x\)-coordinate of \({\text{C}}\) is \(t\).
c.Show that the \(y\)-coordinate of \({\text{C}}\) is \(4 – \frac{1}{2}t\).[2]
Show that the area of \({\text{OBCD}}\) is \(4t – \frac{1}{4}{t^2}\).[3]
The area of \({\text{OBCD}}\) is \(9.75\) square units. Write down a quadratic equation that expresses this information.[1]
(ii) Hence find the correct value for \(t\). Give a reason for your answer.[4]
▶️Answer/Explanation
Markscheme
\({\text{E}}(8{\text{, }}0)\) (A1)(A1)
Notes: Brackets required but do not penalize again if mark lost in Q4 (i)(d). If missing award (A1)(A0).
Accept \(x = 8\), \(y = 0\)
Award (A1) for \(x = 8\)
\(y + \frac{1}{2}t = 4\) (M1)(M1)
Note: (M1) for the equation of the line seen. (M1) for substituting \(t\).
\(y = 4 – \frac{1}{2}t\) (AG)
Note: Final line must be seen or previous (M1) mark is lost.[2 marks]
\({\text{Area}} = \frac{1}{2} \times (4 + 4 – \frac{1}{2}t) \times t\) (M1)(A1)
Note: (M1) for substituting in correct formula, (A1) for correct substitution.
\( = \frac{1}{2} \times (8 – \frac{1}{2}t) \times t = \frac{1}{2}(8t – \frac{1}{2}{t^2})\) (A1)
\( = 4t – \frac{1}{4}{t^2}\) (AG)
Note: Final line must be seen or previous (A1) mark is lost.[3 marks]
\(4t – \frac{1}{4}{t^2} = 9.75\) or any equivalent form. (A1)[1 mark]
(i) \(t = 3\) or \(t =13\) (A1)(ft)(A1)(ft)(G2)
Note: Follow through from candidate’s equation to part (d). Award (A0)(A1)(ft) for \((3{\text{, }}0)\) and \((13{\text{, }}0)\).
(ii) \(t\) must be a value between \(0\) and \(8\) then \(t = 3\)
Note: Accept \({\text{B}}\) is between \({\text{O}}\) and \({\text{E}}\). Do not award (R0)(A1).