Question 5. [Maximum mark: 5]
The number of sick days taken by each employee in a company during a year was recorded. The data was organized in a box and whisker diagram as shown below:
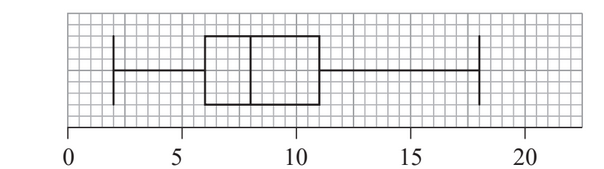
For this data,
(i)write down the minimum number of sick days taken during the year.
(ii)the lower quartile.
(iii)the median. [3]
Paul claims that this box and whisker diagram can be used to infer that the percentage of employees who took fewer than six sick days is smaller than the percentage of employees who took more than eleven sick days.
b. State whether Paul is correct. Justify your answer. [2]
Answer/Explanation
(a) (i) 2 (ii) 6 (iii) 8
(b) EITHER Each of these percentages represent approximately 25% of the employees. OR
The diagram is not explicit enough to show what is happening at the quartiles regarding 6 and 11 / we do not have the data points OR
Discrete data not clear how to interpret “fewer”. THEN Hence, Paul is not correct (OR no such inference can be made).
Question
Leo is investigating whether a six-sided die is fair. He rolls the die 60 times and records the
observed frequencies in the following table:
| Number on die | 1 | 2 | 3 | 4 | 5 | 6 |
| Observed frequency | 8 | 7 | 6 | 15 | 12 | 12 |
Leo carries out a \(X^2\) goodness of fit test at a 5% significance level.
(a) Write down the null and alternative hypotheses.
(b) Write down the degrees of freedom.
(c) Write down the expected frequency of rolling a 1.
(d) Find the p-value for the test.
(e) State the conclusion of the test. Give a reason for your answer.
Answer/Explanation
Ans:
(a) \(H_o\) : The die is fair OR P(any number) = \(\frac{1}{6}\) OR probabilities are equal
\(H_1\) : The die is not fair OR P(any number ) \(\neq = \frac{1}{6}\) OR probabilities are not equal
(b) 5
(c) 10
(d) (p-value=) 0.287 > 0.05
EITHER
Insufficient evidence to reject the null hypothesis
OR
Insufficient evidence to reject that the die is fair.
Question
The table below shows the number of words in the extended essays of an IB class.
Draw a histogram on the grid below for the data in this table.
[3]
Write down the modal group.[1]
The maximum word count is \(4000\) words.
Write down the probability that a student chosen at random is on or over the word count.[2]
Answer/Explanation
Markscheme
(A3) (C3)
Notes: (A3) for correct histogram, (A2) for one error, (A1) for two errors, (A0) for more than two errors.
Award maximum (A2) if lines do not appear to be drawn with a ruler.
Award maximum (A2) if a frequency polygon is drawn.[3 marks]
\({\text{Modal group}} = 3800 \leqslant w < 4000\) (A1) (C1)[1 mark]
\({\text{Probability}} = \frac{3}{{35}}{\text{ }}(0.0857{\text{, }}8.57\% )\) (A1)(A1) (C2)
Note: (A1) for correct numerator (A1) for correct denominator.[2 marks]
Question
The following histogram shows the weights of a number of frozen chickens in a supermarket. The weights are grouped such that \(1 \leqslant {\text{weight}} < 2\), \(2 \leqslant {\text{weight}} < 3\) and so on.
Find the total number of chickens.[1]
Write down the modal group.[1]
Gabriel chooses a chicken at random.
Find the probability that this chicken weighs less than \(4{\text{ kg}}\).[2]
Answer/Explanation
Markscheme
\(96\) (A1) (C1)[1 mark]
\(3 \leqslant {\text{weight}} < 4{\text{ kg}}\) . Accept \(3 – 4{\text{ kg}}\) (A1) (C1)[1 mark]
For adding three heights or subtracting \(14\) from \(96\) (M1)
\(\frac{{82}}{{96}}{\text{ }}(0.854{\text{ or }}\frac{{41}}{{48}}{\text{, }}85.4\% )\) (ft) from (b). (A1)(ft) (C2)[2 marks]
Question
The distribution of the weights, correct to the nearest kilogram, of the members of a football club is shown in the following table.
On the grid below draw a histogram to show the above weight distribution.
[2]
Write down the mid-interval value for the \(40 – 49\) interval.[1]
Find an estimate of the mean weight of the members of the club.[2]
Write down an estimate of the standard deviation of their weights.[1]
Answer/Explanation
Markscheme
(A1)(A1) (C2)
Notes: (A1) for all correct heights, (A1) for all correct end points (\(39.5\), \(49.5\) etc.).
Histogram must be drawn with a ruler (straight edge) and endpoints must be clear.
Award (A1) only if both correct histogram and correct frequency polygon drawn. [2 marks]
\(44.5\) (A1) (C1)
Note: If (b) is given as \(45\) then award
(b) \(45\) (A0)
(c) \(58.8{\text{ kg}}\) (M1)(A1)(ft) or (C2)(ft) if no working seen.
(d) \(8.44\) (C1)
[1 mark]
Unit penalty (UP) applies in this question.
\({\text{Mean}} = \frac{{44.5 \times 6 + 54.5 \times 18 + \ldots }}{{42}}\) (M1)
Note: (M1) for a sum of frequencies multiplied by midpoint values divided by \(42\).
\( = 58.3{\text{ kg}}\) (A1)(ft) (C2)
Note: Award (A1)(A0)(AP) for \(58\).
Note: If (b) is given as \(45\) then award
(b) \(45\) (A0)
(c) \(58.8{\text{ kg}}\) (M1)(A1)(ft) or (C2)(ft) if no working seen.
(d) \(8.44\) (C1)[2 marks]
\({\text{Standard deviation}} = 8.44\) (A1) (C1)
Note: If (b) is given as \(45\) then award
(b) \(45\) (A0)
(c) \(58.8{\text{ kg}}\) (M1)(A1)(ft) or (C2)(ft) if no working seen.
(d) \(8.44\) (C1)[1 mark]
