Question
The number of bottles of water sold at a railway station on each day is given in the following table.
a.Write down
(i) the mean temperature;
(ii) the standard deviation of the temperatures.[2]
b.Write down the correlation coefficient, \(r\), for the variables \(n\) and \(T\).[1]
c.Comment on your value for \(r\).[2]
d.The equation of the line of regression for \(n\) on \(T\) is \(n = dT – 100\).
(i) Write down the value of \(d\).
(ii) Estimate how many bottles of water will be sold when the temperature is \({19.6^ \circ }\).[2]
e.On a day when the temperature was \({36^ \circ }\) Peter calculates that \(314\) bottles would be sold. Give one reason why his answer might be unreliable.[1]
▶️Answer/Explanation
Markscheme
(i) 19.2 (G1)
(ii) 1.45 (G1)[2 marks]
\(r = 0.942\) (G1)[1 mark]
Strong, positive correlation. (A1)(ft)(A1)(ft)[2 marks]
(i) \(d = 11.5\) (G1)
(ii) \(n = 11.5 \times 19.6 – 100\)
\( = 125\) (accept \(126\)) (A1)(ft)
Note: Answer must be a whole number.[2 marks]
It is unreliable to extrapolate outside the values given (outlier). (R1)[1 mark]
Question
In a mountain region there appears to be a relationship between the number of trees growing in the region and the depth of snow in winter. A set of 10 areas was chosen, and in each area the number of trees was counted and the depth of snow measured. The results are given in the table below.
In a study on \(100\) students there seemed to be a difference between males and females in their choice of favourite car colour. The results are given in the table below. A \(\chi^2\) test was conducted.
A, a, i.Use your graphic display calculator to find the mean number of trees.[1]
A, a, iii.Use your graphic display calculator to find the mean depth of snow.[1]
Use your graphic display calculator to find the standard deviation of the depth of snow.[1]
A, b.Write down the product-moment correlation coefficient, r.[2]
A, c.Write down the equation of the regression line of y on x.[2]
A, d.If the number of trees in an area is 55, estimate the depth of snow.[2]
A, e, i.Use the equation of the regression line to estimate the depth of snow in an area with 100 trees.[1]
A, e, ii.Decide whether the answer in (e)(i) is a valid estimate of the depth of snow in the area. Give a reason for your answer.[2]
B, a.Write down the total number of male students.[1]
B, b.Show that the expected frequency for males, whose favourite car colour is blue, is 12.6.[2]
B, c, i.The calculated value of \({\chi ^2}\) is \(1.367\) and the critical value of \({\chi ^2}\) is \(5.99\) at the \(5\%\) significance level.
Write down the null hypothesis for this test.[1]
B, c, ii.The calculated value of \({\chi ^2}\) is \(1.367\) and the critical value of \({\chi ^2}\) is \(5.99\) at the \(5\%\) significance level.
Write down the number of degrees of freedom.[1]
B, c, iv.The calculated value of \({\chi ^2}\) is \(1.367\) and the critical value of \({\chi ^2}\) is \(5.99\) at the \(5\%\) significance level.
Determine whether the null hypothesis should be accepted at the \(5\%\) significance level. Give a reason for your answer.[2]
▶️Answer/Explanation
Markscheme
50 (G1)[1 mark]
30.5 (G1)[1 mark]
12.3 (G1)
Note: Award (A1)(ft) for 13.0 in (iv) but only if 17.7 seen in (a)(ii).[1 mark]
\(r = \frac{{188.5}}{{(16.79 \times 12.33)}}\) (M1)
Note: Award (M1) for using their values in the correct formula.
= 0.911 (accept 0.912, 0.910) (A1)(ft)(G2)[2 marks]
y = 0.669x − 2.95 (G1)(G1)
Note: Award (G1) for 0.669x, (G1) for −2.95. If the answer is not in the form of an equation, award at most (G1)(G0).[2 marks]
Depth = 0.669 × 55 − 2.95 (M1)
= 33.8 (A1)(ft)(G2)(ft)
Note: Follow through from their (c) even if no working seen.[2 marks]
64.0 (accept 63.95, 63.9) (A1)(ft)(G1)(ft)
Note: Follow through from their (c) even if no working seen.[1 mark]
It is not valid. It lies too far outside the values that are given. Or equivalent. (A1)(R1)
Note: Do not award (A1)(R0).[2 marks]
28 (A1)[1 mark]
\(\frac{{28 \times 45}}{{100}}\left( {\frac{{28}}{{100}} \times \frac{{45}}{{100}} \times 100} \right)\) (M1)(A1)(ft)
Note: Award (M1) for correct formula, (A1) for correct substitution.
= 12.6 (AG)
Note: Do not award (A1) unless 12.6 seen.[2 marks]
the favourite car colour is independent of gender. (A1)
Note: Accept there is no association between gender and favourite car colour.
Do not accept ‘not related’ or ‘not correlated’.[1 mark]
\(2\) (A1)[1 marks]
Accept the null hypothesis since \(1.367 < 5.991\) (A1)(ft)(R1)
Note: Allow “Do not reject”. Follow through from their null hypothesis and their critical value.
Full credit for use of \(p\)-values from GDC [\(p = 0.505\)].
Do not award (A1)(R0). Award (R1) for valid comparison.[2 marks]
Question
Francesca is a chef in a restaurant. She cooks eight chickens and records their masses and cooking times. The mass m of each chicken, in kg, and its cooking time t, in minutes, are shown in the following table.
Draw a scatter diagram to show the relationship between the mass of a chicken and its cooking time. Use 2 cm to represent 0.5 kg on the horizontal axis and 1 cm to represent 10 minutes on the vertical axis.[4]
Write down for this set of data
(i) the mean mass, \(\bar m\) ;
(ii) the mean cooking time, \(\bar t\) .[2]
Label the point \({\text{M}}(\bar m,\bar t)\) on the scatter diagram.[1]
Draw the line of best fit on the scatter diagram.[2]
Using your line of best fit, estimate the cooking time, in minutes, for a 1.7 kg chicken.[2]
Write down the Pearson’s product–moment correlation coefficient, r .[2]
Using your value for r , comment on the correlation.[2]
The cooking time of an additional 2.0 kg chicken is recorded. If the mass and cooking time of this chicken is included in the data, the correlation is weak.
(i) Explain how the cooking time of this additional chicken might differ from that of the other eight chickens.
(ii) Explain how a new line of best fit might differ from that drawn in part (d).[2]
▶️Answer/Explanation
Markscheme
(A1) for correct scales and labels (mass or m on the horizontals axis, time or t on the vertical axis)
(A3) for 7 or 8 correctly placed data points
(A2) for 5 or 6 correctly placed data points
(A1) for 3 or 4 correctly placed data points, (A0) otherwise. (A4)
Note: If axes reversed award at most (A0)(A3)(ft). If graph paper not used, award at most (A1)(A0).
(i) 1.91 (kg) (1.9125 kg) (G1)
(ii) 83 (minutes) (G1)
Their mean point labelled. (A1)(ft)
Note: Follow through from part (b). Accept any clear indication of the mean point. For example: circle around point, (m, t), M , etc.
Line of best fit drawn on scatter diagram. (A1)(ft)(A1)(ft)
Notes:Award (A1)(ft) for straight line through their mean point, (A1)(ft) for line of best fit with intercept 9(±2) . The second (A1)(ft) can be awarded even if the line does not reach the t-axis but, if extended, the t-intercept is correct.
75 (M1)(A1)(ft)(G2)
Notes: Accept 74.77 from the regression line equation. Award (M1) for indication of the use of their graph to get an estimate OR for correct substitution of 1.7 in the correct regression line equation t = 38.5m + 9.32.
0.960 (0.959614…) (G2)
Note: Award (G0)(G1)(ft) for 0.95, 0.959
Strong and positive (A1)(ft)(A1)(ft)
Note: Follow through from their correlation coefficient in part (f).
(i) Cooking time is much larger (or smaller) than the other eight (A1)
(ii) The gradient of the new line of best fit will be larger (or smaller) (A1)
Note: Some acceptable explanations may include but are not limited to:
The line of best fit may be further away from the plotted points
It may be steeper than the previous line (as the mean would change)
The t-intercept of the new line is smaller (larger)
Do not accept vague explanations, like:
The new line would vary
It would not go through all points
It would not fit the patterns
The line may be slightly tilted
Question
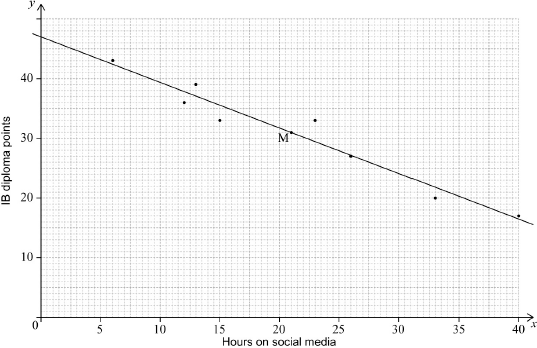
In the month before their IB Diploma examinations, eight male students recorded the number of hours they spent on social media.
For each student, the number of hours spent on social media (\(x\)) and the number of IB Diploma points obtained (\(y\)) are shown in the following table.

Use your graphic display calculator to find
Ten female students also recorded the number of hours they spent on social media in the month before their IB Diploma examinations. Each of these female students spent between 3 and 30 hours on social media.
The equation of the regression line y on x for these ten female students is
\[y = – \frac{2}{3}x + \frac{{125}}{3}.\]
An eleventh girl spent 34 hours on social media in the month before her IB Diploma examinations.
On graph paper, draw a scatter diagram for these data. Use a scale of 2 cm to represent 5 hours on the \(x\)-axis and 2 cm to represent 10 points on the \(y\)-axis.[4]
(i) \({\bar x}\), the mean number of hours spent on social media;
(ii) \({\bar y}\), the mean number of IB Diploma points.[2]
Plot the point \((\bar x,{\text{ }}\bar y)\) on your scatter diagram and label this point M.[2]
Write down the value of \(r\), the Pearson’s product–moment correlation coefficient, for these data.[2]
Write down the equation of the regression line \(y\) on \(x\) for these eight male students.[2]
Draw the regression line, from part (e), on your scatter diagram.[2]
Use the given equation of the regression line to estimate the number of IB Diploma points that this girl obtained.[2]
Write down a reason why this estimate is not reliable.[1]
▶️Answer/Explanation
Markscheme
 (A4)
(A4)
Notes: Award (A1) for correct scale and labelled axes.
Award (A3) for 7 or 8 points correctly plotted,
(A2) for 5 or 6 points correctly plotted,
(A1) for 3 or 4 points correctly plotted.
Award at most (A0)(A3) if axes reversed.
Accept \(x\) and \(y\) sufficient for labelling.
If graph paper is not used, award (A0).
If an inconsistent scale is used, award (A0). Candidates’ points should be read from this scale where possible and awarded accordingly.
A scale which is too small to be meaningful (ie mm instead of cm) earns (A0) for plotted points.[4 marks]
(i) \(\bar x = 21\) (A1)
(ii) \(\bar y = 31\) (A1)[2 marks]
\((\bar x,{\text{ }}\bar y)\) correctly plotted on graph (A1)(ft)
this point labelled M (A1)
Note: Follow through from parts (b)(i) and (b)(ii).
Only accept M for labelling.[2 marks]
\( – 0.973{\text{ }}( – 0.973388 \ldots )\) (G2)
Note: Award (G1) for 0.973, without minus sign.[2 marks]
\(y = – 0.761x + 47.0{\text{ }}(y = – 0.760638 \ldots x + 46.9734 \ldots )\) (A1)(A1)(G2)
Notes: Award (A1) for \( – 0.761x\) and (A1) \( + 47.0\). Award a maximum of (A1)(A0) if answer is not an equation.[2 marks]
line on graph (A1)(ft)(A1)(ft)
Notes: Award (A1)(ft) for straight line that passes through their M, (A1)(ft) for line (extrapolated if necessary) that passes through \((0,{\text{ }}47.0)\).
If M is not plotted or labelled, follow through from part (e).[2 marks]
\(y = – \frac{2}{3}(34) + \frac{{125}}{3}\) (M1)
Note: Award (M1) for correct substitution.
19 (points) (A1)(G2)[2 marks]
extrapolation (R1)
OR
34 hours is outside the given range of data (R1)
Note: Do not accept ‘outlier’.[1 mark]
Question
A group of 800 students answered 40 questions on a category of their choice out of History, Science and Literature.
For each student the category and the number of correct answers, \(N\), was recorded. The results obtained are represented in the following table.
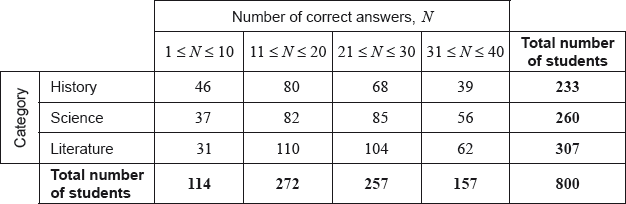
A \({\chi ^2}\) test at the 5% significance level is carried out on the results. The critical value for this test is 12.592.
State whether \(N\) is a discrete or a continuous variable.[1]
Write down, for \(N\), the modal class;[1]
Write down, for \(N\), the mid-interval value of the modal class.[1]
Use your graphic display calculator to estimate the mean of \(N\);[2]
Use your graphic display calculator to estimate the standard deviation of \(N\).[1]
Find the expected frequency of students choosing the Science category and obtaining 31 to 40 correct answers.[2]
Write down the null hypothesis for this test;[1]
Write down the number of degrees of freedom.[1]
Write down the \(p\)-value for the test;[1]
Write down the \({\chi ^2}\) statistic.[2]
State the result of the test. Give a reason for your answer.[2]
▶️Answer/Explanation
Markscheme
discrete (A1)[1 mark]
\(11 \leqslant N \leqslant 20\) (A1)[1 mark]
15.5 (A1)(ft)
Note: Follow through from part (b)(i).[1 mark]
\(21.2{\text{ }}(21.2125)\) (G2)[2 marks]
\(9.60{\text{ }}(9.60428 \ldots )\) (G1)[1 marks]
\(\frac{{260}}{{800}} \times \frac{{157}}{{800}} \times 800\)\(\,\,\,\)OR\(\,\,\,\)\(\frac{{260 \times 157}}{{800}}\) (M1)
Note: Award (M1) for correct substitution into expected frequency formula.
\( = 51.0{\text{ }}(51.025)\) (A1)(G2)[2 marks]
choice of category and number of correct answers are independent (A1)
Notes: Accept “no association” between (choice of) category and number of correct answers. Do not accept “not related” or “not correlated” or “influenced”.[1 mark]
6 (A1)[1 mark]
\(0.0644{\text{ }}(0.0644123 \ldots )\) (G1)[1 mark]
\(11.9{\text{ }}(11.8924 \ldots )\) (G2)[2 marks]
the null hypothesis is not rejected (the null hypothesis is accepted) (A1)(ft)
OR
(choice of) category and number of correct answers are independent (A1)(ft)
as \(11.9 < 12.592\)\(\,\,\,\)OR\(\,\,\,\)\(0.0644 > 0.05\) (R1)
Notes: Award (R1) for a correct comparison of either their \({\chi ^2}\) statistic to the \({\chi ^2}\) critical value or their \(p\)-value to the significance level. Award (A1)(ft) from that comparison.
Follow through from part (f). Do not award (A1)(ft)(R0).[2 marks]
