Question
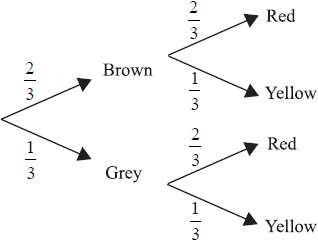
Neil has three dogs. Two are brown and one is grey. When he feeds the dogs, Neil uses three bowls and gives them out randomly. There are two red bowls and one yellow bowl. This information is shown on the tree diagram below.
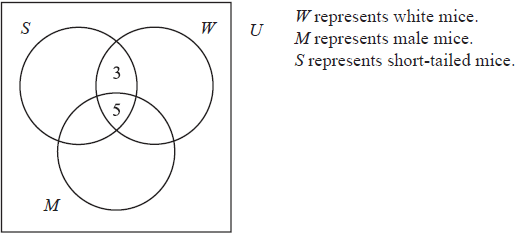
There are 49 mice in a pet shop.
30 mice are white.
27 mice are male.
18 mice have short tails.
8 mice are white and have short tails.
11 mice are male and have short tails.
7 mice are male but neither white nor short-tailed.
5 mice have all three characteristics and
2 have none.
Copy the diagram below to your examination script.
One of the dogs is chosen at random.
(i) Find P (the dog is grey and has the yellow bowl).
(ii) Find P (the dog does not get the yellow bowl).[3]
Neil often takes the dogs to the park after they have eaten. He has noticed that the grey dog plays with a stick for a quarter of the time and both brown dogs play with sticks for half of the time. This information is shown on the tree diagram below.
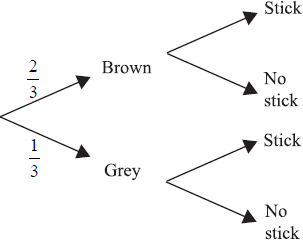
(i) Copy the tree diagram and add the four missing probability values on the branches that refer to playing with a stick.
During a trip to the park, one of the dogs is chosen at random.
(ii) Find P (the dog is grey or is playing with a stick, but not both).
(iii) Find P (the dog is grey given that the dog is playing with a stick).
(iv) Find P (the dog is grey and was fed from the yellow bowl and is not playing with a stick).[9]
Complete the diagram, using the information given in the question.[4]
Find (i) \(n(M \cap W)\)
(ii) \(n(M′ \cup S)\)[3]
Two mice are chosen without replacement.
Find P (both mice are short-tailed).[2]
Answer/Explanation
Markscheme
(i) P (a dog is grey and has the yellow bowl)
\( = \frac{1}{3} \times \frac{1}{3} = \frac{1}{9}( = 0.111)\) (M1)(A1)(G2)
The (M1) is for multiplying two values along any branch of the tree.(ii) P (dog does not get yellow bowl) \( = \frac{2}{3}\) ( = 0.667 (3sf) or 0.6) (A1)[3 marks]
(i) The tree diagram should show the values \(\frac{1}{2},\frac{1}{2}\) for the brown branch and \(\frac{1}{4},\frac{3}{4}\) in the correct positions for the grey branch. (A1)(A1)(ft)
Follow through if the branches are interchanged.
(ii) P (the dog is grey or is playing with a stick, but not both)
\( = \frac{1}{3} \times \frac{3}{4} + \frac{2}{3} \times \frac{1}{2}\) (M1)
\( = \frac{7}{{12}}\) ( = 0.583) (A1)(ft)(G1)
The (M1) is for showing two correct products (whether added or not). Follow through from b(i). Award (M1) for \( \frac{1}{3} + \frac{1}{4}\) (must be a sum).
(iii) P (dog is grey given that it is playing with stick)
\(\frac{{P(G \cap S)}}{{P(S)}} = \frac{{\frac{1}{3} \times \frac{1}{4}}}{{\left( {\frac{2}{3} \times \frac{1}{2}} \right) + \left( {\frac{1}{3} \times \frac{1}{4}} \right)}}\) or \(\frac{1}{{12}}/\frac{5}{{12}}\) (M1)(A1)(ft)
(M1) for substituted conditional probability formula, (A1) for correct substitutions.
\( = \frac{1}{5}\) ( = 0.2) (A1)(ft)(G2)
(iv) P (grey and fed from yellow bowl and not playing with stick) \( = \frac{1}{3} \times \frac{1}{3} \times \frac{3}{4} = \frac{1}{{12}}\) ( = \(\frac{3}{{36}}\) = 0.0833 3sf). (M1)(A1)(ft)(G1)
(M1) is for product of 3 reasonable probability values.[9 marks]
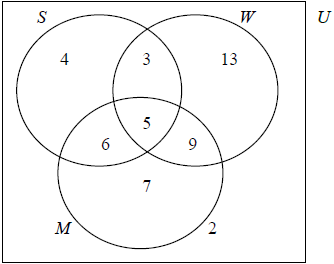(A1)(A1)(A1)(ft)(A1)(ft)
Award (A1) for 2 (must be in a box), (A1) for 7, (A1)(ft) for 6 and 4, (A1)(ft) for 9 and 13. Observe the assignment of (ft) marks strictly here. Example A common error is likely to be 11 instead of 6 (A0). In this case follow through to 4 and 18 (A1)(ft) for the final pair. Here the 4 follows from the total of 27 for n(M).[4 marks]
(i) \(n(M \cap W) = 14\) (A1)(ft)
(ii) \(n(M’ \cup S) = 22 + 11\) OR \(15 + 18\) (A1)(ft)
= 33 (A1)(ft)
Award (A2) if answer 33 is seen. Award (A1) for any of 22, 11, 15 or 18 seen but 33 absent.[3 marks]
P (both mice short-tailed) \( = \frac{{18}}{{49}} \times \frac{{17}}{{48}} = \frac{{306}}{{352}}\) (= 0.130). (M1)(A1)(ft)(G1)
(Allow alternatives such as 153/1176 or 51/392.) Award (M1) for any of \(\frac{{18}}{{49}}\) and \(\frac{{17}}{{48}}\) or \(\frac{{18}}{{49}} \times \frac{{17}}{{49}}\) or \(\frac{{18}}{{49}} + \frac{{17}}{{48}}\) seen.[2 marks]
Question
Sharon and Lisa share a flat. Sharon cooks dinner three nights out of ten. If Sharon does not cook dinner, then Lisa does. If Sharon cooks dinner the probability that they have pasta is 0.75. If Lisa cooks dinner the probability that they have pasta is 0.12.
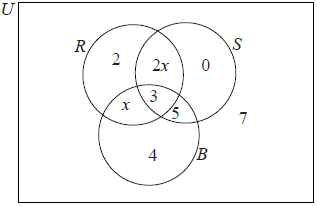
A survey was carried out in a year 12 class. The pupils were asked which pop groups they like out of the Rockers (R), the Salseros (S), and the Bluers (B). The results are shown in the following diagram.
Copy and complete the tree diagram to represent this information.
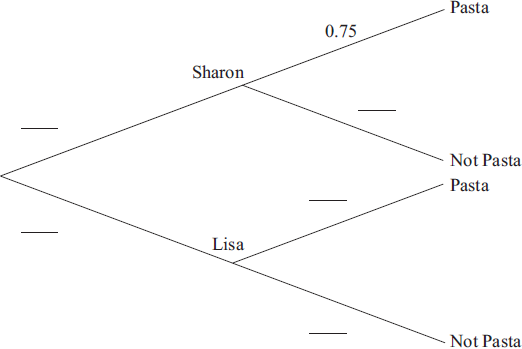[3]
Find the probability that Lisa cooks dinner and they do not have pasta.[2]
Find the probability that they do not have pasta.[3]
Given that they do not have pasta, find the probability that Lisa cooked dinner.[3]
Write down \(n(R \cap S \cap B)\).[1]
Find \(n(R’)\).[2]
Describe which groups the pupils in the set \(S \cap B\) like.[2]
Use set notation to describe the group of pupils who like the Rockers and the Bluers but do not like the Salseros.[2]
There are 33 pupils in the class.
Find x.[2]
There are 33 pupils in the class.
Find the number of pupils who like the Rockers.[1]
Answer/Explanation
Markscheme
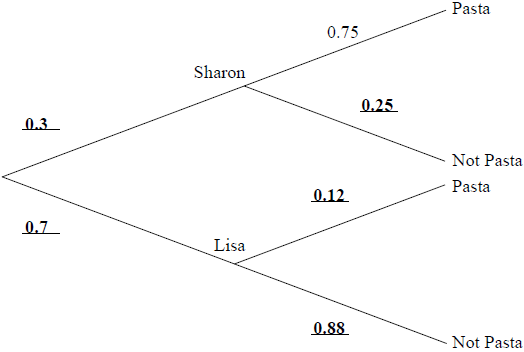
Note: Award (A1) for each correct pair. (A3)[3 marks]
\(0.7 \times 0.88 = 0.616{\text{ }}\left( {\frac{{77}}{{125}},{\text{ }}61.6{\text{ }}\% } \right)\) (M1)(A1)(ft)(G2)
Note: Award (M1) for multiplying the correct probabilities.[2 marks]
\(0.3 \times 0.25 + 0.7 \times 0.88\) (M1)(M1)
Notes: Award (M1) for a relevant two-factor product, could be \(S \times NP\) OR \(L \times NP\).
Award (M1) for summing 2 two-factor products.
\({\text{P}} = 0.691{\text{ }}\left( {\frac{{691}}{{1000}},{\text{ }}69.1{\text{ }}\% } \right)\) (A1)(ft)(G2)
Notes: (ft) from their answer to (b).[3 marks]
\(\frac{{0.616}}{{0.691}}\) (M1)(A1)
Note: Award (M1) for substituted conditional probability formula, (A1) for correct substitution.
\({\text{P}} = 0.891{\text{ }}\left( {\frac{{616}}{{691}},{\text{ }}89.1{\text{ }}\% } \right)\) (A1)(ft)(G2)[3 marks]
3 (A1)[1 mark]
For 5, 4, 7 (0) seen with no extra values (A1)
16 (A1)(G2)[2 marks]
They like (both) the Salseros (S) and they like the Bluers (B) (A1)(A1)
Note: Award (A1) for “and”, (A1) for the correct groups.[2 marks]
\(R \cap B \cap S’\) (A1)(A1)
Note: Award (A1) for \(R \cap B\), (A1) for \( \cap S’\)[2 marks]
\(21+ 3x = 33\) (M1)
\(x = 4\) (A1)(G2)[2 marks]
17 (A1)(ft)[1 mark]
Question
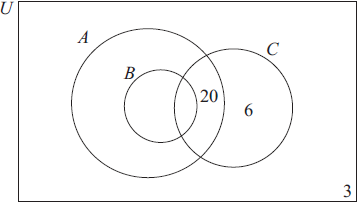
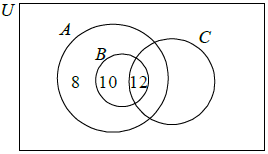
The Venn diagram below represents the students studying Mathematics (A), Further Mathematics (B) and Physics (C) in a school.
50 students study Mathematics
38 study Physics
20 study Mathematics and Physics but not Further Mathematics
10 study Further Mathematics but not Physics
12 study Further Mathematics and Physics
6 study Physics but not Mathematics
3 study none of these three subjects.
Three propositions are given as
p : It is snowing q : The roads are open r : We will go skiing
Copy and complete the Venn diagram on your answer paper.[3]
Write down the number of students who study Mathematics but not Further Mathematics.[1]
Write down the total number of students in the school.[1]
Write down \(n({\text{B}} \cup {\text{C}})\).[2]
Write the following compound statement in symbolic form.
“It is snowing and the roads are not open.”[2]
Write the following compound statement in words.
\((\neg p \wedge q) \Rightarrow r\)[3]
An incomplete truth table for the compound proposition \((\neg p \wedge q) \Rightarrow r\) is given below.
Copy and complete the truth table on your answer paper.
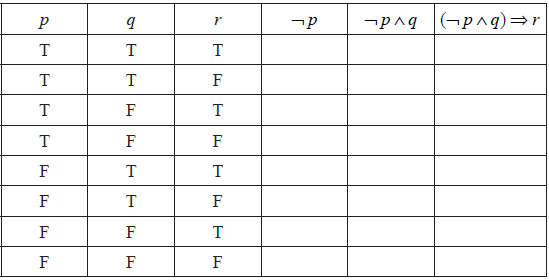[3]
Answer/Explanation
Markscheme
(A1)(A1)(A1)
Note: Award (A1) for each correct number in the correct position.[3 marks]
28 (A1)(ft)
Note: 20 + their 8.[1 mark]
59 (A1)(ft)[1 mark]
10 + 12 + 20 + 6 (M1)
Note: Award (M1) for use of the correct regions.
= 48 (A1)(ft)(G2)
OR
59 − 8 − 3 (M1)
= 48 (A1)(ft)[2 marks]
\(p \wedge \neg q\) (A1)(A1)
Note: Award (A1) for \(\wedge\), (A1) for both statements in the correct order.[2 marks]
If it is not snowing and the roads are open (then) we will go skiing. (A1)(A1)(A1)
Note: Award (A1) for “if…(then)”, (A1) for “not snowing and the roads are open”, (A1) for “we will go skiing”.[3 marks]
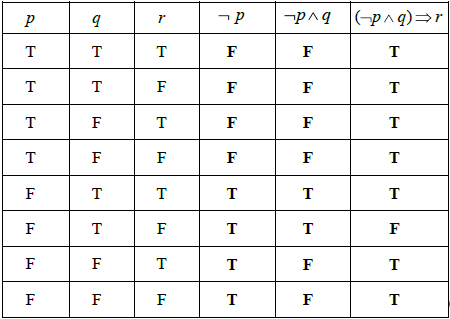(A1)(A1)(ft)(A1)(ft)
Note: Award (A1) for each correct column.[3 marks]
Question
One day the numbers of customers at three cafés, “Alan’s Diner” ( \(A\) ), “Sarah’s Snackbar” ( \(S\) ) and “Pete’s Eats” ( \(P\) ), were recorded and are given below.
17 were customers of Pete’s Eats only
27 were customers of Sarah’s Snackbar only
15 were customers of Alan’s Diner only
10 were customers of Pete’s Eats and Sarah’s Snackbar but not Alan’s Diner
8 were customers of Pete’s Eats and Alan’s Diner but not Sarah’s Snackbar
Some of the customers in each café were given survey forms to complete to find out if they were satisfied with the standard of service they received.
Draw a Venn Diagram, using sets labelled \(A\) , \(S\) and \(P\) , that shows this information.[3]
There were 48 customers of Pete’s Eats that day. Calculate the number of people who were customers of all three cafés.[2]
There were 50 customers of Sarah’s Snackbar that day. Calculate the total number of people who were customers of Alan’s Diner.[3]
Write down the number of customers of Alan’s Diner that were also customers of Pete’s Eats.[1]
Find \(n[(S \cup P) \cap A’]\).[2]
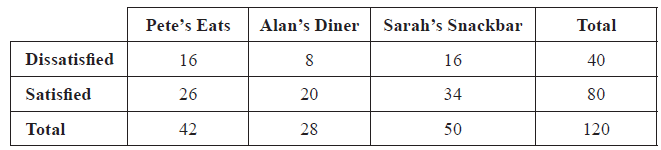
One of the survey forms was chosen at random, find the probability that the form showed “Dissatisfied”;[2]
One of the survey forms was chosen at random, find the probability that the form showed “Satisfied” and was completed at Sarah’s Snackbar;[2]
One of the survey forms was chosen at random, find the probability that the form showed “Dissatisfied”, given that it was completed at Alan’s Diner.[2]
A \({\chi ^2}\) test at the \(5\% \) significance level was carried out to determine whether there was any difference in the level of customer satisfaction in each of the cafés.
Write down the null hypothesis, \({{\text{H}}_0}\) , for the \({\chi ^2}\) test.[1]
A \({\chi ^2}\) test at the \(5\% \) significance level was carried out to determine whether there was any difference in the level of customer satisfaction in each of the cafés.
Write down the number of degrees of freedom for the test.[1]
A \({\chi ^2}\) test at the \(5\% \) significance level was carried out to determine whether there was any difference in the level of customer satisfaction in each of the cafés.
Using your graphic display calculator, find \({\chi ^2}_{calc}\) .[2]
A \({\chi ^2}\) test at the \(5\% \) significance level was carried out to determine whether there was any difference in the level of customer satisfaction in each of the cafés.
State, giving a reason, the conclusion to the test.[2]
Answer/Explanation
Markscheme
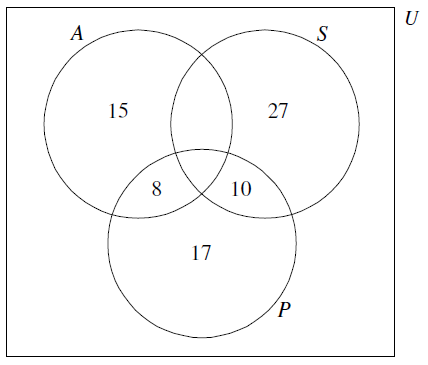
(A1) for rectangle and three labelled intersecting circles
(A1) for \(15\), \(27\) and \(17\)
(A1) for \(10\) and \(8\) (A3)[3 marks]
\(48 – (8 +10 +17)\) or equivalent (M1)
\( = 13\) (A1)(ft)(G2)[2 marks]
\(50 – (27 +10 +13)\) (M1)
Note: Award (M1) for working seen.
\( = 0\) (A1)
number of elements in A \(= 36\) (A1)(ft)(G3)
Note: Follow through from (b).[3 marks]
\(21\) (A1)(ft)
Note: Follow through from (b) even if no working seen.[1 mark]
\(54\) (M1)(A1)(ft)(G2)
Note: Award (M1) for \(17\), \(10\), \(27\) seen. Follow through from (a).[2 marks]
\(\frac{{40}}{{120}}{\text{ }}\left( {\frac{1}{3}{\text{, }}0.333{\text{, }}33.3\% } \right)\) (A1)(A1)(G2)
Note: Award (A1) for numerator, (A1) for denominator.[2 marks]
\(\frac{{34}}{{120}}{\text{ }}\left( {\frac{{17}}{{60}}{\text{, }}0.283{\text{, }}28.3\% } \right)\) (A1)(A1)(G2)
Note: Award (A1) for numerator, (A1) for denominator.[2 marks]
\(\frac{8}{{28}}{\text{ }}\left( {\frac{2}{7}{\text{, }}0.286{\text{, }}28.6\% } \right)\) (A1)(A1)(G2)
Note: Award (A1) for numerator, (A1) for denominator.[2 marks]
customer satisfaction is independent of café (A1)
Note: Accept “customer satisfaction is not associated with the café”.[1 mark]
\(2\) (A1)[1 mark]
\(0.754\) (G2)
Note: Award (G1)(G1)(AP) for \(0.75\) or for correct answer incorrectly rounded to 3 s.f. or more, (G0) for \(0.7\).[2 marks]
since \({\chi ^2}_{calc} < {\chi ^2}_{crit}5.991 accept (or Do not reject) H0 (R1)(A1)(ft)
Note: Follow through from their value in (e).
OR
Accept (or Do not reject) H0 as \(p\)-value \((0.686) > 0.05\) (R1)(A1)(ft)
Notes: Do not award (A1)(R0). Award the (R1) for comparison of appropriate values.[2 marks]