Question 1 [Maximum mark: 19]
A medical centre is testing patients for a certain disease. This disease occurs in 5 % of the population.
They test every patient who comes to the centre on a particular day.
a. State the sampling method being used. [1]
It is intended that if a patient has the disease, they test “positive”, and if a patient does not have the disease, they test “negative”.
However, the tests are not perfect, and only 99 % of people who have the disease test positive. Also, 2 % of people who do not have the disease test positive.
The tree diagram shows some of this information.
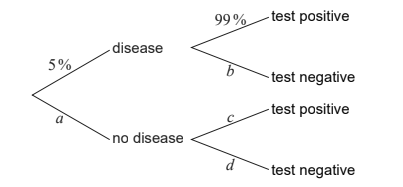
b. Write down the value of
(i) a .
(ii) b .
(iii) c .
(iv) d . [4]
c. Use the tree diagram to find the probability that a patient selected at random
(i) will not have the disease and will test positive.
(ii) will test negative.
(iii) has the disease given that they tested negative. [8]
d. The medical centre finds the actual number of positive results in their sample is different than predicted by the tree diagram. Explain why this might be the case. [1]
The staff at the medical centre looked at the care received by all visiting patients on a randomly chosen day. All the patients received at least one of these services: they had medical tests (M), were seen by a nurse (N), or were seen by a doctor (D). It was found that:
- 78 had medical tests,
- 45 were seen by a nurse;
- 30 were seen by a doctor;
- 9 had medical tests and were seen by a doctor and a nurse;
- 18 had medical tests and were seen by a doctor but were not seen by a nurse;
- 11 patients were seen by a nurse and had medical tests but were not seen by a doctor;
- 2 patients were seen by a doctor without being seen by nurse and without having medical tests.
(e) Draw a Venn diagram to illustrate this information, placing all relevant information on the diagram. [3]
(f) Find the total number of patients who visited the centre during this day. [2]
Answer/Explanation
(a) convenience sampling
(b) (i) 95% (ii) 1% (iii) 2%(iv) 98%
(c) (i) 0.95 × 0.02 0.019 (ii) 0.05 × 0.01 + 0.95 × 0.98 \(\rightarrow 0.932 (0.9315)\)
(iii) recognition of conditional probability
(iii) \(\frac{0.5\times 0.01}{0.05\times 0.0.+0.95\times 0.98}\) 0.000537 (0.000536768…)
(d) EITHER sample may not be representative of population OR sample is not randomly selected OR unrealistic to think expected and observed values will be exactly equal
(e)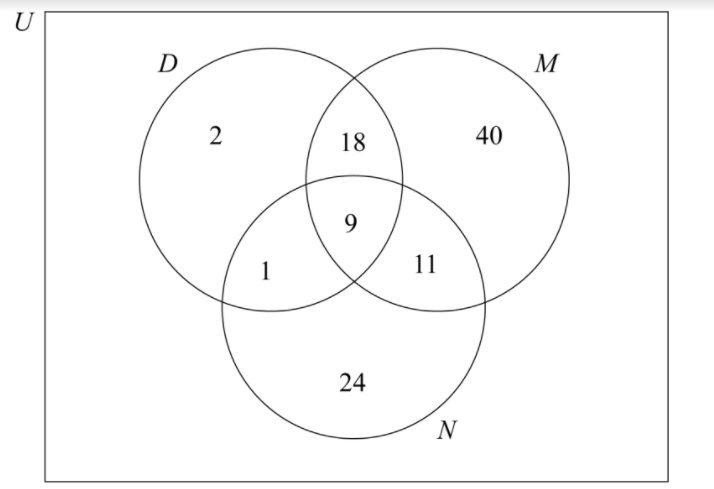 
(f) \(18 + 9 + 1 + 11 + 2 + 40 + 24 =105\)
Question
On a school excursion, 100 students visited an amusement park. The amusement park’s main attractions are rollercoasters (R), water slides (W ), and virtual reality rides (V ).
The students were asked which main attractions they visited. The results are shown in the Venn diagram.
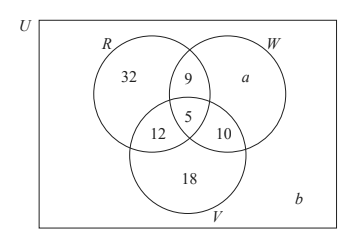
A total of 74 students visited the rollercoasters or the water slides.
(i) Find the value of a .
(ii) Find the value of b . [4]
Find the number of students who visited at least two types of main attraction. [2]
Write down the value of n(R∩W). . [1]
Find the probability that a randomly selected student visited
the rollercoasters;
the virtual reality rides. [3]
Hence determine whether the events in parts (d)(i) and (d)(ii) are independent.
Justify your reasoning. [2]
Answer/Explanation
Ans:
(a)
(i) 74 −(32 +12+10+9+5) OR 74 − 68
(a =)6
(ii) 100 – (74+18)
OR
100 − 92
OR
100 – (32+9+5 12+10+ 18+6)
(b)9+5+12+10
36
(c)14
(d)
(i)\(\frac{58}{100}(\frac{29}{50}\),0.58,58%)
(ii) \(\frac{45}{100}(\frac{9}{20},0.45,45%)\))
(e) they are not independent \(\frac{58}{100}\times \frac{45}{100 }\neq\frac{17}{100}\)OR 0.26. 0.261 ≠ 0.17
Question
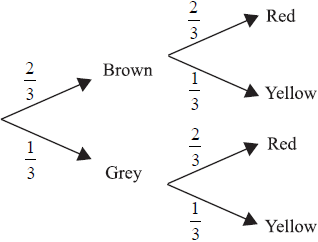
Neil has three dogs. Two are brown and one is grey. When he feeds the dogs, Neil uses three bowls and gives them out randomly. There are two red bowls and one yellow bowl. This information is shown on the tree diagram below.
There are 49 mice in a pet shop.
30 mice are white.
27 mice are male.
18 mice have short tails.
8 mice are white and have short tails.
11 mice are male and have short tails.
7 mice are male but neither white nor short-tailed.
5 mice have all three characteristics and
2 have none.
Copy the diagram below to your examination script.
One of the dogs is chosen at random.
(i) Find P (the dog is grey and has the yellow bowl).
(ii) Find P (the dog does not get the yellow bowl).[3]
Neil often takes the dogs to the park after they have eaten. He has noticed that the grey dog plays with a stick for a quarter of the time and both brown dogs play with sticks for half of the time. This information is shown on the tree diagram below.
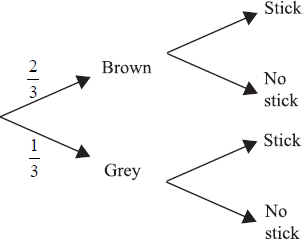
(i) Copy the tree diagram and add the four missing probability values on the branches that refer to playing with a stick.
During a trip to the park, one of the dogs is chosen at random.
(ii) Find P (the dog is grey or is playing with a stick, but not both).
(iii) Find P (the dog is grey given that the dog is playing with a stick).
(iv) Find P (the dog is grey and was fed from the yellow bowl and is not playing with a stick).[9]
Complete the diagram, using the information given in the question.[4]
Find (i) \(n(M \cap W)\)
(ii) \(n(M′ \cup S)\)[3]
Two mice are chosen without replacement.
Find P (both mice are short-tailed).[2]
Answer/Explanation
Markscheme
(i) P (a dog is grey and has the yellow bowl)
\( = \frac{1}{3} \times \frac{1}{3} = \frac{1}{9}( = 0.111)\) (M1)(A1)(G2)
The (M1) is for multiplying two values along any branch of the tree.
(ii) P (dog does not get yellow bowl) \( = \frac{2}{3}\) ( = 0.667 (3sf) or 0.6) (A1)[3 marks]
(i) The tree diagram should show the values \(\frac{1}{2},\frac{1}{2}\) for the brown branch and \(\frac{1}{4},\frac{3}{4}\) in the correct positions for the grey branch. (A1)(A1)(ft)
Follow through if the branches are interchanged.
(ii) P (the dog is grey or is playing with a stick, but not both)
\( = \frac{1}{3} \times \frac{3}{4} + \frac{2}{3} \times \frac{1}{2}\) (M1)
\( = \frac{7}{{12}}\) ( = 0.583) (A1)(ft)(G1)
The (M1) is for showing two correct products (whether added or not). Follow through from b(i). Award (M1) for \( \frac{1}{3} + \frac{1}{4}\) (must be a sum).
(iii) P (dog is grey given that it is playing with stick)
\(\frac{{P(G \cap S)}}{{P(S)}} = \frac{{\frac{1}{3} \times \frac{1}{4}}}{{\left( {\frac{2}{3} \times \frac{1}{2}} \right) + \left( {\frac{1}{3} \times \frac{1}{4}} \right)}}\) or \(\frac{1}{{12}}/\frac{5}{{12}}\) (M1)(A1)(ft)
(M1) for substituted conditional probability formula, (A1) for correct substitutions.
\( = \frac{1}{5}\) ( = 0.2) (A1)(ft)(G2)
(iv) P (grey and fed from yellow bowl and not playing with stick) \( = \frac{1}{3} \times \frac{1}{3} \times \frac{3}{4} = \frac{1}{{12}}\) ( = \(\frac{3}{{36}}\) = 0.0833 3sf). (M1)(A1)(ft)(G1)
(M1) is for product of 3 reasonable probability values.[9 marks]
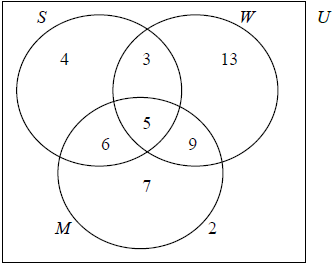(A1)(A1)(A1)(ft)(A1)(ft)
Award (A1) for 2 (must be in a box), (A1) for 7, (A1)(ft) for 6 and 4, (A1)(ft) for 9 and 13. Observe the assignment of (ft) marks strictly here. Example A common error is likely to be 11 instead of 6 (A0). In this case follow through to 4 and 18 (A1)(ft) for the final pair. Here the 4 follows from the total of 27 for n(M).[4 marks]
(i) \(n(M \cap W) = 14\) (A1)(ft)
(ii) \(n(M’ \cup S) = 22 + 11\) OR \(15 + 18\) (A1)(ft)
= 33 (A1)(ft)
Award (A2) if answer 33 is seen. Award (A1) for any of 22, 11, 15 or 18 seen but 33 absent. [3 marks]
P (both mice short-tailed) \( = \frac{{18}}{{49}} \times \frac{{17}}{{48}} = \frac{{306}}{{352}}\) (= 0.130). (M1)(A1)(ft)(G1)
(Allow alternatives such as 153/1176 or 51/392.) Award (M1) for any of \(\frac{{18}}{{49}}\) and \(\frac{{17}}{{48}}\) or \(\frac{{18}}{{49}} \times \frac{{17}}{{49}}\) or \(\frac{{18}}{{49}} + \frac{{17}}{{48}}\) seen.[2 marks]
Question
When Geraldine travels to work she can travel either by car (C), bus (B) or train (T). She travels by car on one day in five. She uses the bus 50 % of the time. The probabilities of her being late (L) when travelling by car, bus or train are 0.05, 0.12 and 0.08 respectively.
It is not necessary to use graph paper for this question.
Copy the tree diagram below and fill in all the probabilities, where NL represents not late, to represent this information.
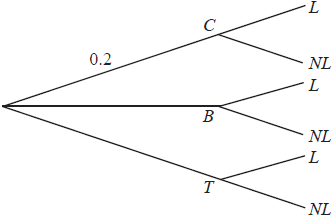[5]
Find the probability that Geraldine travels by bus and is late.[1]
Find the probability that Geraldine is late.[3]
Find the probability that Geraldine travelled by train, given that she is late.[3]
Sketch the curve of the function \(f (x) = x^3 − 2x^2 + x − 3\) for values of \(x\) from −2 to 4, giving the intercepts with both axes.[3]
On the same diagram, sketch the line \(y = 7 − 2x\) and find the coordinates of the point of intersection of the line with the curve.[3]
Find the value of the gradient of the curve where \(x = 1.7\) .[2]
Answer/Explanation
Markscheme
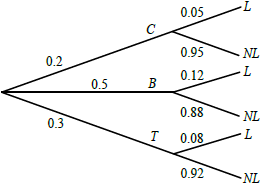
Award (A1) for 0.5 at B, (A1) for 0.3 at T, then (A1) for each correct pair. Accept fractions or percentages. (A5)[5 marks]
0.06 (accept \(0.5 \times 0.12\) or 6%) (A1)(ft)[1 mark]
for a relevant two-factor product, either \(C \times L\) or \(T \times L\) (M1)
for summing three two-factor products (M1)
\((0.2 \times 0.05 + 0.06 + 0.3 \times 0.08)\)
0.094 (A1)(ft)(G2)[3 marks]
\(\frac{{0.3 \times 0.08}}{{0.094}}\) (M1)(A1)(ft)
award (M1) for substituted conditional probability formula seen, (A1)(ft) for correct substitution
= 0.255 (A1)(ft)(G2)[3 marks]
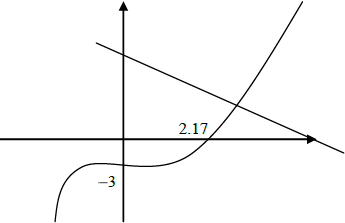(G3)[3 marks]
line drawn with –ve gradient and +ve y-intercept (G1)
(2.45, 2.11) (G1)(G1)[3 marks]
\(f ‘ (1.7) = 3(1.7)^2 – 4(1.7) + 1\) (M1)
award (M1) for substituting in their \(f’ (x)\)
2.87 (A1)(G2)[2 marks]
Question
A group of 50 students completed a questionnaire for a Mathematical Studies project. The following data was collected.
\(18\) students own a digital camera (D)
\(15\) students own an iPod (I)
\(26\) students own a cell phone (C)
\(1\) student owns all three items
\(5\) students own a digital camera and an iPod but not a cell phone
\(2\) students own a cell phone and an iPod but not a digital camera
\(3\) students own a cell phone and a digital camera but not an iPod
Claire and Kate both wish to go to the cinema but one of them has to stay at home to baby-sit.
The probability that Kate goes to the cinema is \(0.2\). If Kate does not go Claire goes.
If Kate goes to the cinema the probability that she is late home is \(0.3\).
If Claire goes to the cinema the probability that she is late home is \(0.6\).
Represent this information on a Venn diagram.[4]
Calculate the number of students who own none of the items mentioned above.[2]
If a student is chosen at random, write down the probability that the student owns a digital camera only.[1]
If two students are chosen at random, calculate the probability that they both own a cell phone only.[3]
If a student owns an iPod, write down the probability that the student also owns a digital camera.[2]
Copy and complete the probability tree diagram below.
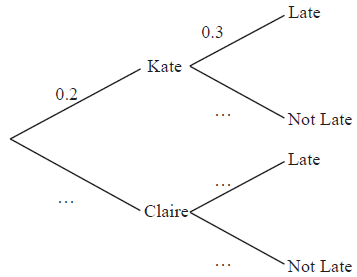[3]
Calculate the probability that
(i) Kate goes to the cinema and is not late;
(ii) the person who goes to the cinema arrives home late.
Answer/Explanation
Markscheme
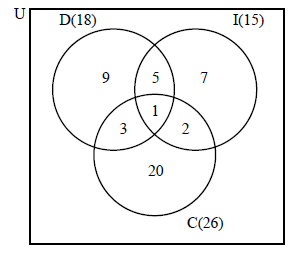(A1)(A1)(A1)(A1)(ft)
Note: (A1) for rectangle with 3 intersecting circles, (A1) for \(1\), (A1) for \(5\), \(3\), \(2\), (A1)(ft) for \(9\), \(7\), \(20\) if subtraction is carried out, or \(18\), \(15\), \(26\) seen by the letters D, I and C.[4 marks]
\(50 – 47\) (M1)
Note: (M1) for subtracting their value from \(50\).
\( = 3\) (A1)(ft)(G2)[2 marks]
\(\frac{9}{{50}}\) (A1)(ft)[1 mark]
\(\frac{{20}}{{50}} \times \frac{{19}}{{49}}\) (A1)(ft)(M1)
\( = \frac{{38}}{{245}}{\text{ }}\left( {\frac{{380}}{{2450}}{\text{, }}0.155{\text{, }}15.5\% } \right)\) (A1)(ft)(G2)
Notes: (A1)(ft) for correct fractions from their Venn diagram
(M1) for multiplying their fractions
(A1)(ft) for correct answer.[3 marks]
\(\frac{6}{{15}}{\text{ }}\left( {\frac{2}{5}{\text{, }}0.4{\text{, }}40\% } \right)\) (A1)(ft)(A1)(ft)
Note: (A1)(ft) for numerator, (A1)(ft) denominator.[2 marks]
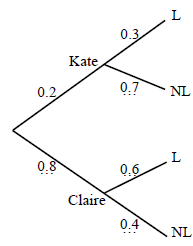(A1)(A1)(A1)
Note: (A1) for \(0.8\), (A1) for \(0.7\), (A1) for \(0.6\) and \(0.4\).[3 marks]
(i) \(0.2 \times 0.7 = 0.14\) (M1)(A1)(ft)(G2)
Note: (M1) for multiplying correct numbers.[2 marks]
(ii) \(0.2 \times 0.3 + 0.8 \times 0.6\) (M1)(M1)
\( = 0.54\) (A1)(ft)(G3)
Note: (M1) for each correct product (use candidate’s tree), (A1)(ft) for answer.[3 marks]