Question 8. [Maximum mark: 7]
A game is played where two unbiased dice are rolled and the score in the game is the greater of the two numbers shown. If the two numbers are the same, then the score in the game is the number shown on one of the dice. A diagram showing the possible outcomes is given below.
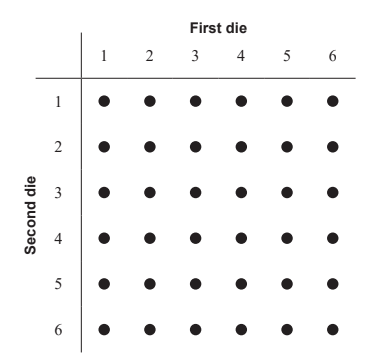
Let T be the random variable “the score in a game”.
(a) Complete the table to show the probability distribution of T . [2]
t | 1 | 2 | 3 | 4 | 5 | 6 |
P(T = t) |
(b) Find the probability that
(i)a player scores at least 3 in a game.
(ii) a player scores 6, given that they scored at least 3. [3]
()Find the expected score of a game. [2]
▶️Answer/Explanation
(a) 
- Note: Award A1 if three to five probabilities are correct. (b) (i) \(\frac{32}{36}(\frac{8}{9},0.888888…, 88.9%)\) (ii) use of conditional probability \(\frac{11}{32}\) (0.34375,34.4%) (c)\(\frac{1 \times 1+3\times 2+5\times 3+…+11\times 6}{36}= \frac{161}{36}(4.4477222…)\)
- e.g. denominator of 32
Question
Karl has three brown socks and four black socks in his drawer. He takes two socks at random
from the drawer.
(a) Complete the tree diagram.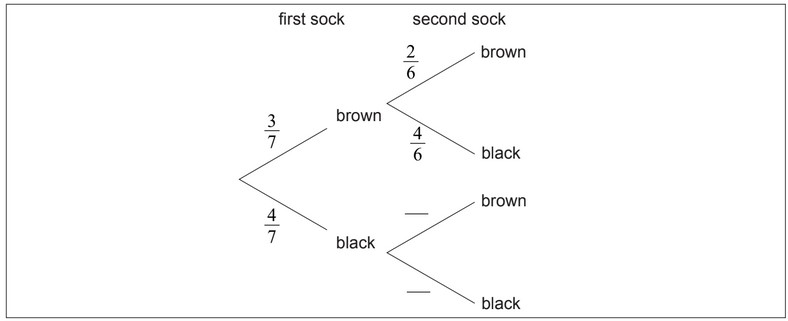
(b) Find the probability that Karl takes two socks of the same colour.
(c) Given that Karl has two socks of the same colour find the probability that he has two
brown socks.
▶️Answer/Explanation
Ans:
(a)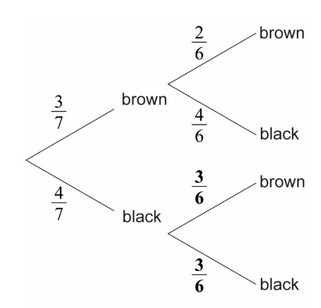 
(b) multiplying along branches and then adding outcomes
\(\frac{3}{7} \times \frac{2}{6} + \frac{4}{7} \times \frac{3}{6}\)
\(=\frac{18}{42}(=\frac{3}{7} \approx 0.429 (42.9%))\)
(c) use of conditional probability formula
\(\frac{(\frac{3}{7} \times \frac{2}{6})}{(\frac{3}{7})}\)
\(=\frac{6}{18}(=\frac{1}{3})(\frac{252}{756},0.333, 33.3%)\)
Question
4. Karl has three brown socks and four black socks in his drawer. He takes two socks at random
from the drawer.
(a) Complete the tree diagram.
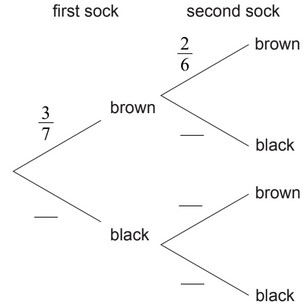
(b) Find the probability that Karl takes two socks of the same colour.
(c) Given that Karl has two socks of the same colour find the probability that he has two
brown socks.
▶️Answer/Explanation
Ans:
(a)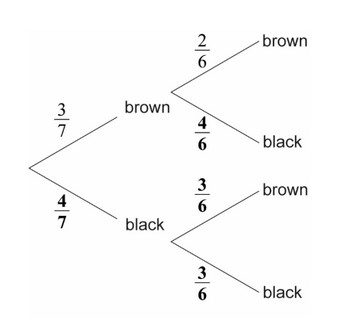 
(b) multiplying along branches and then adding outcomes
\(\frac{3}{7} \times \frac{2}{6} + \frac{4}{7} \times \frac{3}{6}\)
\(=\frac{18}{42} (= \frac{3}{7} \approx 0.429 (42.9 %))\)
(c) use of conditional probability formula
\(\frac{(\frac{3}{7} \times \frac{2}{6})}{(\frac{3}{7})}\)
\(=\frac{6}{18} (=\frac{1}{3}) (\frac{252}{756}, 0.333, 33.3%)\)
Question
When Andy plays tennis, \(65\% \) of his first serves go into the correct area of the court.
If the first serve goes into the correct area, his chance of winning the point is \(90\% \).
If his first serve does not go into the correct area, Andy is allowed a second serve and, of these, \(80\% \) go into the correct area.
If the second serve goes into the correct area, his chance of winning the point is \(60\% \).
If neither serve goes into the correct area, Andy loses the point.
a.Complete the tree diagram below.
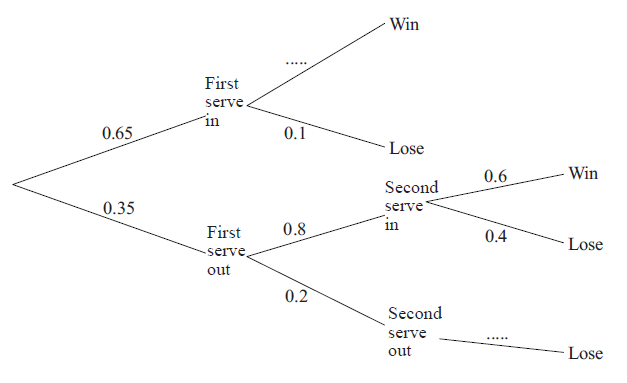[2]
b.Find the probability that Andy loses the point.[4]
▶️Answer/Explanation
Markscheme
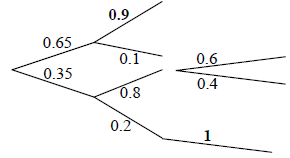(A1)(A1) (C2)[2 marks]
\(0.65 \times 0.1\) (\( = 0.065\)) (A1)
\(0.35 \times 0.8 \times 0.4\) (\( = 0.112\)) (A1)
\(0.35 \times 0.2 \times 1\) the 1 can be implied (\( = 0.07\)) (A1)(ft)
0.247 (A1)(ft) (C4)
Note: No (ft) for any probabilities greater than 1.[4 marks]