Question
The strength of earthquakes is measured on the Richter magnitude scale, with values
typically between 0 and 8 where 8 is the most severe.
The Gutenberg–Richter equation gives the average number of earthquakes per year, N,
which have a magnitude of at least M. For a particular region the equation is
\(log_{10}N=a-M\), for some \(a\epsilon \mathbb{R}\).
This region has an average of 100 earthquakes per year with a magnitude of at least 3.
(a) Find the value of a.
The equation for this region can also be written as \(N=\frac{b}{M^M}\).
(b) Find the value of b.
(c) Given 0<M<8, find the range for N.
The expected length of time, in years, between earthquakes with a magnitude of at least M is \(\frac{1}{N}\).
Within this region the most severe earthquake recorded had a magnitude of 7.2.
(d) Find the expected length of time between this earthquake and the next earthquake of at least this magnitude. Give your answer to the nearest year.
▶️Answer/Explanation
Ans:
(a) \(log_{10} 100 = a – 3\)
a = 5
(b) EITHER
\(N = 10^{5-M}\)
OR
\(100=\frac{b}{10^3}\)
THEN
b = 100000\((=10^5)\)
(c) 0.001<N<100000 \((10^{-3}<N<10^5)\)
(d) \(N=\frac{10^5}{10^{7.2}}(=0.0063095…)\)
length of time = \(\frac{1}{0.0063095…}=10^{2.2}\)
= 158 years
Question
The following diagram shows part of the curve C with parametric equations
x =t3, y = t2 – 1, t ∈ \(\mathbb{R}\).
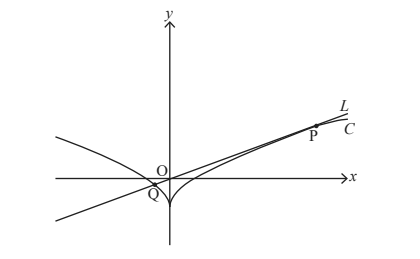
The line L passes through the origin O and is tangential to C at the point P( p3 , p2 –1) ,
where p > 0 . The line L intersects C again at the point Q .
Determine
the equation of L , giving the gradient in its exact form.
the exact coordinates of P . [8]
Determine the exact coordinates of Q . [5]
▶️Answer/Explanation
Ans:
(i)
METHOD 1
\(\frac{dy}{dx}= \frac{dy/dp}{dx/dp}\)
\(=\frac{2p}{3p^2}\)
\(=\frac{2}{3p}\)
the equation of the tangent at P is
\(y- p^{2}+ 1 = \frac{2}{3p}(x-p^{3})\)
this passes through the origin if
\(-p^{2}+ 1 = \frac{2p^{3}}{3p}\)
\(p= \sqrt{3}\)
the equation of L is
y= \(\frac{2}{3\sqrt{3}x}\)
METHOD 2
the point of intersection of the line y = mx and C satisfies t2– 1 = mt3
giving \(mt^3-t^2+1=0\)
the condition for tangency is that this cubic has a double root. The condition for that is that the cubic has a stationary value on the t-axis consider
\(3mt^{2}-2t= 0\)
\(t = \frac{3}{2m}\) (rejecting t = 0)
therefor \(m(\frac{3}{2m})^{3}- (\frac{3}{2m})^{2}+1 =0\)
\(m^{2}= \frac{4}{9}-\frac{8}{27}= \frac{4}{27}\)
\(m= \frac{2}{3\sqrt{3}}\)
so the tangent is \(y = \frac{2}{3\sqrt{3}x}\)
(ii) teh coordinates of are \((3\sqrt{3.2})\)
(b) the tangent meets C where
\(t^{2}-1=\frac{2}{3\sqrt{3}} t^{3}\)
\( t^{3}- \frac{3\sqrt{3}}{2}t^{2}+ \frac{3\sqrt{3}}{2}=0\)
it is known that this cubic has a double root \( t=\sqrt{3}\) so considering the product (or sum) of roots or by factorising
third root = \(- \frac{\sqrt{3}}{2} \)
Q is \((-\frac{3\sqrt{3}}{8},-\frac{1}{4})\)
Question
Find the equation of the tangent to the curve y = e2x – 3x at the point where x = 0 . [Maximum mark: 5]
▶️/Explanation
Ans:
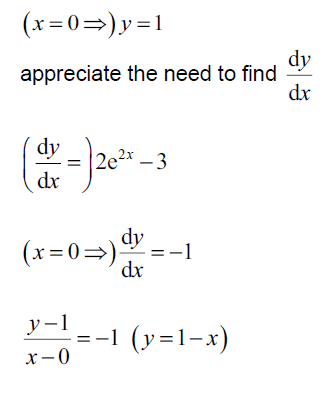
Question
Consider the functions f (x) = -(x – h)2 + 2k and g(x) = e x-2 + k where h , k ∈ R.
(a) Find f ′(x). [1]
The graphs of f and g have a common tangent at x = 3
(b) Show that h + = \(\frac{e+6}{2}\) [3]
(c) Hence, show that k = \(e+ \frac{e^{2}}{4}\) [3]
▶️Answer/Explanation
Ans
(a) f ‘( x) = −2( x − h)
(a) f (x) = -2 (x-h )
(b)
g (x) = e x-2 OR (3) = e 3-2 (may be seen anywhere)
recognizing f ‘(3) = g’ (3)
-2 (3-h ) = e 3-2 (=e)
-6+ 2h = e OR 3-h = – \(\frac{e}{2}\)
Note: The final A1 is dependent on one of the previous marks being awarded. h =\(\frac{e+6}{2}\)
(c) f( 3) = g (3)
– (3 – h )2 + 2k = e 3-2 + k correct equation in k
EITHER
\(-(3- \frac{e+6}{2})^{2}+ 2k \) = e 3-2+ k
k = e+ \((\frac{6-e-6}{2})^{2}(-e+({\frac{-e}{2}})^2)\)
OR
k = e + \((3- \frac{e+6}{2})^2\)
k = e+ 9 -3e -18 + \(\frac{e^2+12e+36}{4}\)
THEN k= e + \(\frac{e^2}{4}\)
Question
A normal to the graph of \(y = \arctan (x – 1)\) , for \(x > 0\), has equation \(y = – 2x + c\) , where \(x \in \mathbb{R}\) .
Find the value of c.
▶️Answer/Explanation
Markscheme
\(\frac{{\text{d}}}{{{\text{d}}x}}\left( {\arctan (x – 1)} \right) = \frac{1}{{1 + {{(x – 1)}^2}}}\) (or equivalent) A1
\({m_N} = – 2{\text{ and so }}{m_T} = \frac{1}{2}\) (R1)
Attempting to solve \(\frac{1}{{1 + {{(x – 1)}^2}}} = \frac{1}{2}\) (or equivalent) for x M1
\(x = 2{\text{ (as }}x > 0)\) A1
Substituting \(x = 2\) and \(y = \frac{\pi }{4}\) to find c M1
\(c = 4 + \frac{\pi }{4}\) A1 N1
[6 marks]
Examiners report
There was a disappointing response to this question from a fair number of candidates. The differentiation was generally correctly performed, but it was then often equated to \( – 2x + c\) rather than the correct numerical value. A few candidates either didn’t simplify arctan(1) to \(\frac{\pi }{4}\), or stated it to be 45 or \(\frac{\pi }{2}\).
