IB Mathematics SL 5.6 Local maximum and minimum points AI SL Paper 2 - Exam Style Questions - New Syllabus
Question
The solid shown in the following diagram is comprised of a cylinder and two hemispheres. The cylinder has height \(h\) cm and radius \(x\) cm. The hemispheres fit exactly onto either end of the cylinder.
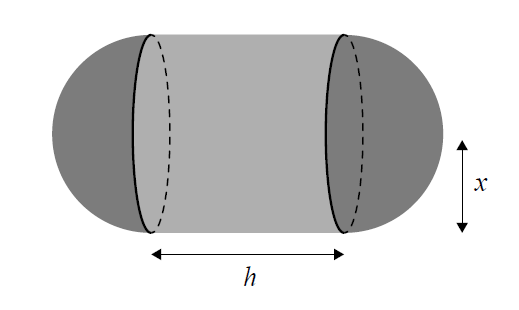

The volume of the cylinder is \(41\text{ cm}^3\).
(a) Show that the total surface area, \(S\text{ cm}^2\), of the solid is given by \( \displaystyle S=\frac{82}{x}+4\pi x^2\). [3]
The total surface area of the solid has a local maximum or a local minimum value when \(x=a\).
(b) (i) Find an expression for \( \displaystyle \frac{dS}{dx}\).
(ii) Hence, find the exact value of \(a\). [5]
(ii) Hence, find the exact value of \(a\). [5]
(c) (i) Find an expression for \( \displaystyle \frac{d^2S}{dx^2}\).
(ii) Use the second derivative of \(S\) to justify that \(S\) is a minimum when \(x=a\).
(iii) Find the minimum surface area of the solid. [6]
(ii) Use the second derivative of \(S\) to justify that \(S\) is a minimum when \(x=a\).
(iii) Find the minimum surface area of the solid. [6]
▶️ Answer/Explanation
Markscheme (with brief working)
(a)
Curved area of cylinder \(=2\pi xh\). Surface area of two hemispheres \(=\) surface area of a sphere \(=4\pi x^2\).
Volume condition for cylinder: \(\pi x^2 h=41 \Rightarrow h=\dfrac{41}{\pi x^2}\).
Hence \[ S=2\pi x\!\left(\frac{41}{\pi x^2}\right)+4\pi x^2 =\frac{82}{x}+4\pi x^2. \] M1 A1 A1 (AG)
Volume condition for cylinder: \(\pi x^2 h=41 \Rightarrow h=\dfrac{41}{\pi x^2}\).
Hence \[ S=2\pi x\!\left(\frac{41}{\pi x^2}\right)+4\pi x^2 =\frac{82}{x}+4\pi x^2. \] M1 A1 A1 (AG)
(b)
(i) Differentiate: \[ \frac{dS}{dx}=-\frac{82}{x^2}+8\pi x. \] A1 A1
(ii) Stationary when \(\dfrac{dS}{dx}=0\): \[ -\frac{82}{x^2}+8\pi x=0 \;\Rightarrow\;8\pi x^3=82 \;\Rightarrow\; x^3=\frac{41}{4\pi}. \] Hence \[ \boxed{a=\left(\frac{41}{4\pi}\right)^{\!1/3}}. \] M1 A1 A1
(ii) Stationary when \(\dfrac{dS}{dx}=0\): \[ -\frac{82}{x^2}+8\pi x=0 \;\Rightarrow\;8\pi x^3=82 \;\Rightarrow\; x^3=\frac{41}{4\pi}. \] Hence \[ \boxed{a=\left(\frac{41}{4\pi}\right)^{\!1/3}}. \] M1 A1 A1
(c)
(i) Second derivative: \[ \frac{d^2S}{dx^2}=\frac{164}{x^3}+8\pi. \] A1 A1
(ii) Justifying a minimum (two acceptable methods):
- Method 1 (substitution): Using \(a^3=\dfrac{41}{4\pi}\), \[ \frac{d^2S}{dx^2}\Big|_{x=a} =\frac{164}{a^3}+8\pi =164\cdot\frac{4\pi}{41}+8\pi =16\pi+8\pi =24\pi\;(>0). \] Therefore \(S\) has a local minimum at \(x=a\). M1 A1 (AG)
- Method 2 (shape of \(S”\)): Sketch or note \(\dfrac{d^2S}{dx^2}=\dfrac{164}{x^3}+8\pi>0\) for \(x>0\); thus \(S\) is convex and the stationary point at \(x=a\) is a minimum. M1 A1 (AG)
(iii) Minimum surface area \(S_{\min}=S(a)\): \[ S(a)=\frac{82}{a}+4\pi a^2 =82\!\left(\frac{4\pi}{41}\right)^{\!1/3} +4\pi\!\left(\frac{41}{4\pi}\right)^{\!2/3} =\boxed{3(4\pi)^{1/3}41^{2/3}\ \text{cm}^2} \approx \boxed{82.9\ \text{cm}^2}. \] (Exact form shown; decimal rounded to 3 s.f.) M1 A1
Total Marks: 14
