Question
Given \(f (x) = x^2 − 3x^{−1}, x \in {\mathbb{R}}, – 5 \leqslant x \leqslant 5, x \ne 0\),
A football is kicked from a point A (a, 0), 0 < a < 10 on the ground towards a goal to the right of A.
The ball follows a path that can be modelled by part of the graph
\(y = − 0.021x^2 + 1.245x − 6.01, x \in {\mathbb{R}}, y \geqslant 0\).
x is the horizontal distance of the ball from the origin
y is the height above the ground
Both x and y are measured in metres.
Write down the equation of the vertical asymptote.[1]
Find \(f ′(x)\).[2]
Using your graphic display calculator or otherwise, write down the coordinates of any point where the graph of \(y = f (x)\) has zero gradient.[2]
Write down all intervals in the given domain for which \(f (x)\) is increasing.[3]
Using your graphic display calculator or otherwise, find the value of a.[1]
Find \(\frac{{dy}}{{dx}}\).[2]
(i) Use your answer to part (b) to calculate the horizontal distance the ball has travelled from A when its height is a maximum.
(ii) Find the maximum vertical height reached by the football.[4]
Draw a graph showing the path of the football from the point where it is kicked to the point where it hits the ground again. Use 1 cm to represent 5 m on the horizontal axis and 1 cm to represent 2 m on the vertical scale.[4]
The goal posts are 35 m from the point where the ball is kicked.
At what height does the ball pass over the goal posts?[2]
Answer/Explanation
Markscheme
equation of asymptote is x = 0 (A1)
(Must be an equation.)
[1 mark]
\(f ‘(x) = 2x + 3x^{-2}\) (or equivalent) (A1) for each term (A1)(A1)
[2 marks]
stationary point (–1.14, 3.93) (G1)(G1)(ft)
(-1,4) or similar error is awarded (G0)(G1)(ft). Here and also as follow through in part (d) accept exact values \( – {\left( {\frac{3}{2}} \right)^{\frac{1}{3}}}\)for the x coordinate and \(3{\left( {\frac{3}{2}} \right)^{\frac{2}{3}}}\) for the y coordinate.
OR \(2x + \frac{3}{{{x^2}}} = 0\) or equivalent
Correct coordinates as above (M1)
Follow through from candidate’s \(f ′(x)\). (A1)(ft)
[2 marks]
In all alternative answers for (d), follow through from candidate’s x coordinate in part (c).
Alternative answers include:
–1.14 ≤ x < 0, 0 < x < 5 (A1)(A1)(ft)(A1)
OR [–1.14,0), (0,5)
Accept alternative bracket notation for open interval ] [. (Union of these sets is not correct, award (A2) if all else is right in this case.)
OR \( – 1.14 \leqslant x < 5,x \ne 0\)
In all versions 0 must be excluded (A1). -1.14 must be the left bound . 5 must be the right bound (A1). For \(x \geqslant – 1.14\) or \(x > – 1.14\) alone, award (A1). For \( – 1.4 \leqslant x < 0\) together with \(x > 0\) award (A2).
[3 marks]
a = 5.30 (3sf) (Allow (5.30, 0) but 5.3 receives an (AP).) (A1)
[1 mark]
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = – 0.042x + 1.245\) (A1) for each term. (A1)(A1)
[2 marks]
Unit penalty (UP) is applicable where indicated in the left hand column.
(i) Maximum value when \(f ‘ (x) = 0\), \( – 0.042x + 1.245 = 0\), (M1)
(M1) is for either of the above but at least one must be seen.
(x = 29.6.)
Football has travelled 29.6 – 5.30 = 24.3 m (3sf) horizontally. (A1)(ft)
For answer of 24.3 m with no working or for correct subtraction of 5.3 from candidate’s x-coordinate at the maximum (if not 29.6), award (A1)(d).
(UP) (ii) Maximum vertical height, f (29.6) = 12.4 m (M1)(A1)(ft)(G2)
(M1) is for substitution into f of a value seen in part (c)(i). f(24.3) with or without evaluation is awarded (M1)(A0). For any other value without working, award (G0). If lines are seen on the graph in part (d) award (M1) and then (A1) for candidate’s value \( \pm 0.5\) (3sf not required.)
[4 marks]
(not to scale)
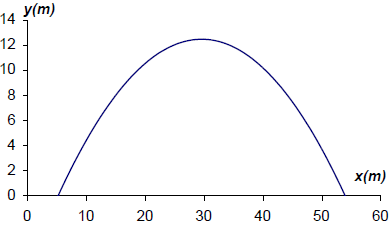(A1)(A1)(A1)(ft)(A1)(ft)
Award (A1) for labels (units not required) and scale, (A1)(ft) for max(29.6,12.4), (A1)(ft) for x-intercepts at 5.30 and 53.9, (all coordinates can be within 0.5), (A1) for well-drawn parabola ending at the x-intercepts.
[4 marks]
Unit penalty (UP) is applicable where indicated in the left hand column.
(UP) f (40.3) = 10.1 m (3sf).
Follow through from (a). If graph used, award (M1) for lines drawn and (A1) for candidate’s value \( \pm 0.5\). (3sf not required). (M1)(A1)(ft)(G2)
[2 marks]
Question
The diagram below shows the graph of a line \(L\) passing through (1, 1) and (2 , 3) and the graph \(P\) of the function \(f (x) = x^2 − 3x − 4\)
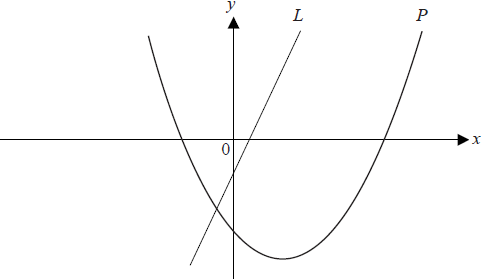
Find the gradient of the line L.[2]
Differentiate \(f (x)\) .[2]
Find the coordinates of the point where the tangent to P is parallel to the line L.[3]
Find the coordinates of the point where the tangent to P is perpendicular to the line L.[4]
Find
(i) the gradient of the tangent to P at the point with coordinates (2, − 6).
(ii) the equation of the tangent to P at this point.[3]
State the equation of the axis of symmetry of P.[1]
Find the coordinates of the vertex of P and state the gradient of the curve at this point.[3]
Answer/Explanation
Markscheme
for attempt at substituted \(\frac{{ydistance}}{{xdistance}}\) (M1)
gradient = 2 (A1)(G2)
[2 marks]
\(2x – 3\) (A1)(A1)
(A1) for \(2x\) , (A1) for \(-3\)
[2 marks]
for their \(2x – 3 =\) their gradient and attempt to solve (M1)
\(x = 2.5\) (A1)(ft)
\(y = -5.25\) ((ft) from their x value) (A1)(ft)(G2)
[3 marks]
for seeing \(\frac{{ – 1}}{{their(a)}}\) (M1)
solving \(2x – 3 = – \frac{1}{2}\) (or their value) (M1)
x = 1.25 (A1)(ft)(G1)
y = – 6.1875 (A1)(ft)(G1)
[4 marks]
(i) \(2 \times 2 – 3 = 1\) ((ft) from (b)) (A1)(ft)(G1)
(ii) \(y = mx + c\) or equivalent method to find \(c \Rightarrow -6 = 2 + c\) (M1)
\(y = x – 8\) (A1)(ft)(G2)
[3 marks]
\(x = 1.5\) (A1)
[1 mark]
for substituting their answer to part (f) into the equation of the parabola (1.5, −6.25) accept x = 1.5, y = −6.25 (M1)(A1)(ft)(G2)
gradient is zero (accept \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0\)) (A1)
[3 marks]
Question
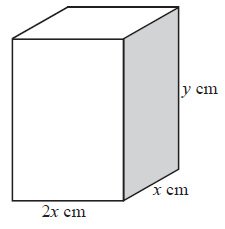
A closed rectangular box has a height \(y{\text{ cm}}\) and width \(x{\text{ cm}}\). Its length is twice its width. It has a fixed outer surface area of \(300{\text{ c}}{{\text{m}}^2}\) .
Factorise \(3{x^2} + 13x – 10\).[2]
Solve the equation \(3{x^2} + 13x – 10 = 0\).[2]
Consider a function \(f(x) = 3{x^2} + 13x – 10\) .
Find the equation of the axis of symmetry on the graph of this function.[2]
Consider a function \(f(x) = 3{x^2} + 13x – 10\) .
Calculate the minimum value of this function.[2]
Show that \(4{x^2} + 6xy = 300\).[2]
Find an expression for \(y\) in terms of \(x\).[2]
Hence show that the volume \(V\) of the box is given by \(V = 100x – \frac{4}{3}{x^3}\).[2]
Find \(\frac{{{\text{d}}V}}{{{\text{d}}x}}\).[2]
(i) Hence find the value of \(x\) and of \(y\) required to make the volume of the box a maximum.
(ii) Calculate the maximum volume.[5]
Answer/Explanation
Markscheme
\((3x – 2)(x + 5)\) (A1)(A1)
[2 marks]
\((3x – 2)(x + 5) = 0\)
\(x = \frac{2}{3}\) or \(x = – 5\) (A1)(ft)(A1)(ft)(G2)
[2 marks]
\(x = \frac{{ – 13}}{6}{\text{ }}( – 2.17)\) (A1)(A1)(ft)(G2)
Note: (A1) is for \(x = \), (A1) for value. (ft) if value is half way between roots in (b).
[2 marks]
Minimum \(y = 3{\left( {\frac{{ – 13}}{6}} \right)^2} + 13\left( {\frac{{ – 13}}{6}} \right) – 10\) (M1)
Note: (M1) for substituting their value of \(x\) from (c) into \(f(x)\) .
\( = – 24.1\) (A1)(ft)(G2)
[2 marks]
\({\text{Area}} = 2(2x)x + 2xy + 2(2x)y\) (M1)(A1)
Note: (M1) for using the correct surface area formula (which can be implied if numbers in the correct place). (A1) for using correct numbers.
\(300 = 4{x^2} + 6xy\) (AG)
Note: Final line must be seen or previous (A1) mark is lost.
[2 marks]
\(6xy = 300 – 4{x^2}\) (M1)
\(y = \frac{{300 – 4{x^2}}}{{6x}}\) or \(\frac{{150 – 2{x^2}}}{{3x}}\) (A1)
[2 marks]
\({\text{Volume}} = x(2x)y\) (M1)
\(V = 2{x^2}\left( {\frac{{300 – 4{x^2}}}{{6x}}} \right)\) (A1)(ft)
\( = 100x – \frac{4}{3}{x^3}\) (AG)
Note: Final line must be seen or previous (A1) mark is lost.
[2 marks]
\(\frac{{{\text{d}}V}}{{{\text{d}}x}} = 100 – \frac{{12{x^2}}}{3}\) or \(100 – 4{x^2}\) (A1)(A1)
Note: (A1) for each term.
[2 marks]
Unit penalty (UP) is applicable where indicated in the left hand column
(i) For maximum \(\frac{{{\text{d}}V}}{{{\text{d}}x}} = 0\) or \(100 – 4{x^2} = 0\) (M1)
\(x = 5\) (A1)(ft)
\(y = \frac{{300 – 4{{(5)}^2}}}{{6(5)}}\) or \(\left( {\frac{{150 – 2{{(5)}^2}}}{{3(5)}}} \right)\) (M1)
\( = \frac{{20}}{3}\) (A1)(ft)
(UP) (ii) \(333\frac{1}{3}{\text{ c}}{{\text{m}}^3}{\text{ }}(333{\text{ c}}{{\text{m}}^3})\)
Note: (ft) from their (e)(i) if working for volume is seen.
[5 marks]
Question
Consider the function \(f:x \mapsto \frac{{kx}}{{{2^x}}}\).
The cost per person, in euros, when \(x\) people are invited to a party can be determined by the function
\(C(x) = x + \frac{{100}}{x}\)
Given that \(f(1) = 2\), show that \(k = 4\).
Write down the values of \(q\) and \(r\) for the following table.
[2]
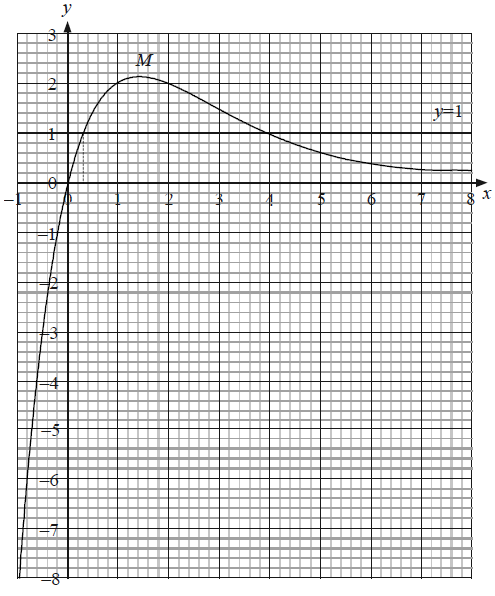
As \(x\) increases from \( – 1\), the graph of \(y = f(x)\) reaches a maximum value and then decreases, behaving asymptotically.
Draw the graph of \(y = f(x)\) for \( – 1 \leqslant x \leqslant 8\). Use a scale of \({\text{1 cm}}\) to represent 1 unit on both axes. The position of the maximum, \({\text{M}}\), the \(y\)-intercept and the asymptotic behaviour should be clearly shown.[4]
Using your graphic display calculator, find the coordinates of \({\text{M}}\), the maximum point on the graph of \(y = f(x)\).[2]
Write down the equation of the horizontal asymptote to the graph of \(y = f(x)\).[2]
(i) Draw and label the line \( y = 1\) on your graph.
(ii) The equation \(f(x) = 1\) has two solutions. One of the solutions is \(x = 4\). Use your graph to find the other solution.[4]
Find \(C'(x)\).[3]
Show that the cost per person is a minimum when \(10\) people are invited to the party.[2]
Calculate the minimum cost per person.[2]
Answer/Explanation
Markscheme
\(f(1) = \frac{k}{{{2^1}}}\) (M1)
Note: (M1) for substituting \(x = 1\) into the formula.
\(\frac{k}{2} = 2\) (M1)
Note: (M1) for equating to 2.
\(k = 4\) (AG)
[2 marks]
\(q = 2\), \(r = 0.125\) (A1)(A1)
[2 marks]
(A4)
Notes: (A1) for scales and labels.
(A1) for accurate smooth curve passing through \((0, 0)\) drawn at least in the given domain.
(A1) for asymptotic behaviour (curve must not go up or cross the \(x\)-axis).
(A1) for indicating the position of the maximum point.
[4 marks]
\({\text{M}}\) (\(1.44\), \(2.12\)) (G1)(G1)
Note: Brackets required, if missing award (G1)(G0). Accept \(x = 1.44\) and \(y = 2.12\).
[2 marks]
\(y = 0\) (A1)(A1)
Note: (A1) for ‘\(y = \)’ provided the right hand side is a constant. (A1) for 0.
[2 marks]
(i) See graph (A1)(A1)
Note: (A1) for correct line, (A1) for label.
(ii) \(x = 0.3\) (ft) from candidate’s graph. (A2)(ft)
Notes: Accept \( \pm 0.1\) from their x. For \(0.310\) award (G1)(G0). For other answers taken from the GDC and not given correct to 3 significant figures award (G0)(AP)(G0) or (G1)(G0) if (AP) already applied.
[4 marks]
\(C'(x) = 1 – \frac{{100}}{{{x^2}}}\) (A1)(A1)(A1)
Note: (A1) for 1, (A1) for \( – 100\) , (A1) for \({x^2}\) as denominator or \({{x^{ – 2}}}\) as numerator. Award a maximum of (A2) if an extra term is seen.
[3 marks]
For studying signs of the derivative at either side of \(x = 10\) (M1)
For saying there is a change of sign of the derivative (M1)(AG)
OR
For putting \(x = 10\) into \(C’\) and getting zero (M1)
For clear sketch of the function or for mentioning that the function changes from decreasing to increasing at \(x = 10\) (M1)(AG)
OR
For solving \(C'(x) = 0\) and getting \(10\) (M1)
For clear sketch of the function or for mentioning that the function changes from decreasing to increasing at \(x = 10\) (M1)(AG)
Note: For a sketch with a clear indication of the minimum or for a table with values of \(x\) at either side of \(x = 10\) award (M1)(M0).
[2 marks]
\(C(10) = 10 + \frac{{100}}{{10}}\) (M1)
\(C(10) = 20\) (A1)(G2)
[2 marks]
Question
Consider the function \(f(x) = 3x + \frac{{12}}{{{x^2}}},{\text{ }}x \ne 0\).
Differentiate \(f (x)\) with respect to \(x\).[3]
Calculate \(f ′(x)\) when \(x = 1\).[2]
Use your answer to part (b) to decide whether the function, \(f\) , is increasing or decreasing at \(x = 1\). Justify your answer.[2]
Solve the equation \(f ′(x) = 0\).[3]
The graph of f has a local minimum at point P. Let T be the tangent to the graph of f at P.
Write down the coordinates of P.[2]
The graph of f has a local minimum at point P. Let T be the tangent to the graph of f at P.
Write down the gradient of T.[1]
The graph of f has a local minimum at point P. Let T be the tangent to the graph of f at P.
Write down the equation of T.[2]
Sketch the graph of the function f, for −3 ≤ x ≤ 6 and −7 ≤ y ≤ 15. Indicate clearly the point P and any intercepts of the curve with the axes.[4]
On your graph draw and label the tangent T.[2]
T intersects the graph of f at a second point. Write down the x-coordinate of this point of intersection.[1]
Answer/Explanation
Markscheme
\(f’ (x) = 3 – \frac{24}{x^3}\) (A1)(A1)(A1)
Note: Award (A1) for 3, (A1) for –24, (A1) for x3 (or x−3). If extra terms present award at most (A1)(A1)(A0).
[3 marks]
\(f ‘(1) = -21\) (M1)(A1)(ft)(G2)
Note: (ft) from their derivative only if working seen.
[2 marks]
Derivative (gradient, slope) is negative. Decreasing. (R1)(A1)(ft)
Note: Do not award (R0)(A1).
[2 marks]
\(3 – \frac{{24}}{{{x^3}}} = 0\) (M1)
\(x^3 = 8\) (A1)
\(x = 2\) (A1)(ft)(G2)
[3 marks]
(2, 9) (Accept x = 2, y = 9) (A1)(A1)(G2)
Notes: (ft) from their answer in (d).
Award (A1)(A0) if brackets not included and not previously penalized.
[2 marks]
0 (A1)
[1 mark]
y = 9 (A1)(A1)(ft)(G2)
Notes: Award (A1) for y = constant, (A1) for 9.
Award (A1)(ft) for their value of y in (e)(i).
[2 marks]
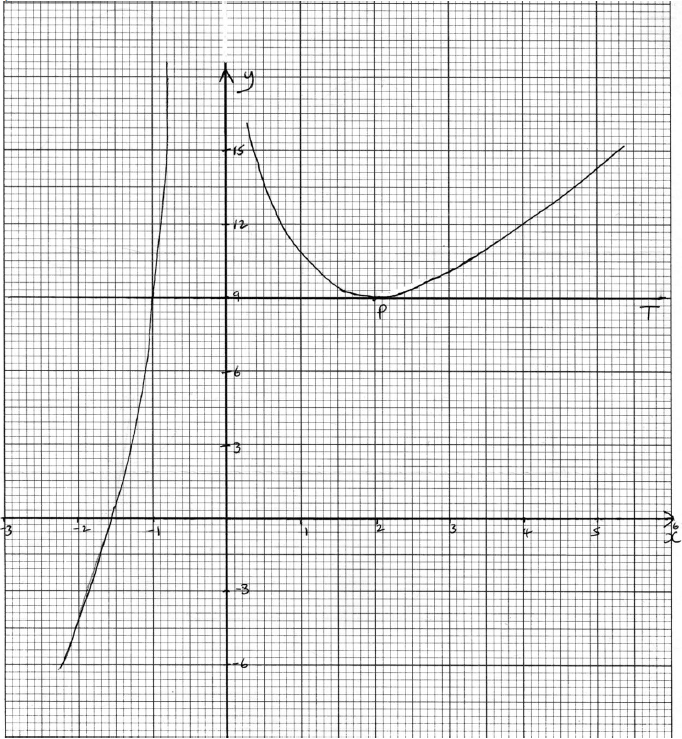(A4)
Notes: Award (A1) for labels and some indication of scale in the stated window.
Award (A1) for correct general shape (curve must be smooth and must not cross the y-axis).
Award (A1) for x-intercept seen in roughly the correct position.
Award (A1) for minimum (P).
[4 marks]
Tangent drawn at P (line must be a tangent and horizontal). (A1)
Tangent labeled T. (A1)
Note: (ft) from their tangent equation only if tangent is drawn and answer is consistent with graph.
[2 marks]
x = −1 (G1)(ft)
[1 mark]