Question
A function f is of the form \(f(t)=pe^{q cos (rt)},p, q, r \epsilon \mathbb{R}^+\). Part of the graph of f is shown.
The points A and B have coordinates A(0 , 6.5) and B(5.2 , 0.2), and lie on f .
The point A is a local maximum and the point B is a local minimum.
Find the value of p, of q and of r.
▶️Answer/Explanation
Ans:

Question
Consider the curve \(y = 2x(4- e^x)\).
(a) Find
(i) \(\frac{dy}{dx}\).
(ii) \(\frac{d^2y}{dx^2}\).
The curve has a point of inflexion at (a, b).
(b) Find the value of a.
▶️Answer/Explanation
Ans:
(a) (i) use of product
\(\frac{dy}{dx}=2(4-e^x)+2x(-e^x)\)
\(=8 – 2e^x – 2xe^x\)
(ii) use of product rule
\(\frac{d^2y}{dx^2}=-2e^x – 2e^x – 2xe^x\)
\(=-4e^x – 2xe^x\)
\(=-2(2+x)e^x\)
(b) \(-2(2+a)e^a = 0\) OR sketch \(\frac{d^2y}{dx^2}\) with x-intercept indicated
OR finding the local maximum of \(\frac{dy}{dx}\) at (-2, 8.27)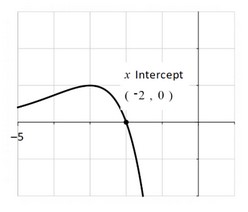
(a=) -2
Question
A slope field for the differential equation \(\frac{dy}{dx}=x^2 + \frac{y}{2}\) is shown.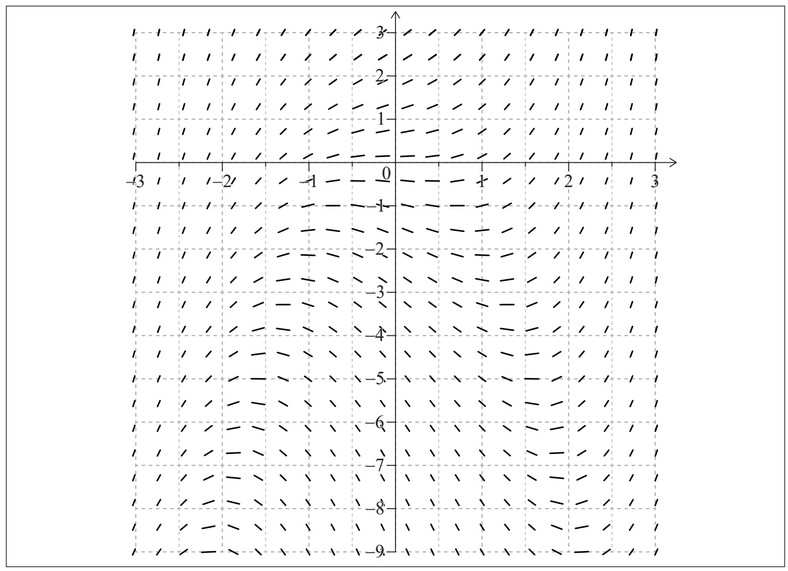
Some of the solutions to the differential equation have a local maximum point and a local
minimum point.
(a) (i) Write down the equation of the curve on which all these maximum and minimum points lie.
(ii) Sketch this curve on the slope field.
The solution to the differential equation that passes through the point (0 , −2) has both a
local maximum point and a local minimum point.
(b) On the slope field, sketch the solution to the differential equation that passes
through (0, −2).
▶️Answer/Explanation
Ans:
(a) (i) \(x^2+\frac{y}{2}=0 (y=-2x^2)\)
(ii) \(y=-2x^2\) drawn on diagram (correct shape with a maximum at (0, 0))
(b)
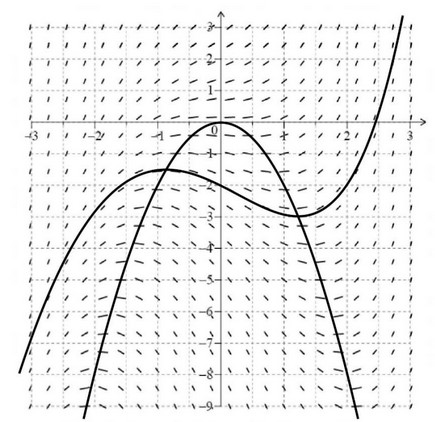
correct shape with a local maximum and minimum, passing through (0, 2)
local maximum and minimum on the graph of \(y=-2x^2\)
Question
Consider the curve \(y = 2x(4- e^x)\).
(a) Find
(i) \(\frac{dy}{dx}\).
(ii) \(\frac{d^2y}{dx^2}\).
The curve has a point of inflexion at (a, b).
(b) Find the value of a.
▶️Answer/Explanation
Ans:
(a) (i) use of product
\(\frac{dy}{dx}=2(4-e^x)+2x(-e^x)\)
\(=8 – 2e^x – 2xe^x\)
(ii) use of product rule
\(\frac{d^2y}{dx^2}=-2e^x – 2e^x – 2xe^x\)
\(=-4e^x – 2xe^x\)
\(=-2(2+x)e^x\)
(b) \(-2(2+a)e^a = 0\) OR sketch \(\frac{d^2y}{dx^2}\) with x-intercept indicated
OR finding the local maximum of \(\frac{dy}{dx}\) at (-2, 8.27)
(a=) -2
Question
A slope field for the differential equation \(\frac{dy}{dx}=x^2 + \frac{y}{2}\) is shown.
Some of the solutions to the differential equation have a local maximum point and a local
minimum point.
(a) (i) Write down the equation of the curve on which all these maximum and minimum points lie.
(ii) Sketch this curve on the slope field.
The solution to the differential equation that passes through the point (0 , −2) has both a
local maximum point and a local minimum point.
(b) On the slope field, sketch the solution to the differential equation that passes
through (0, −2).
▶️Answer/Explanation
Ans:
(a) (i) \(x^2+\frac{y}{2}=0 (y=-2x^2)\)
(ii) \(y=-2x^2\) drawn on diagram (correct shape with a maximum at (0, 0))
(b)

correct shape with a local maximum and minimum, passing through (0, 2)
local maximum and minimum on the graph of \(y=-2x^2\)
