Question
A modern art painting is contained in a square frame. The painting has a shaded region
bounded by a smooth curve and a horizontal line.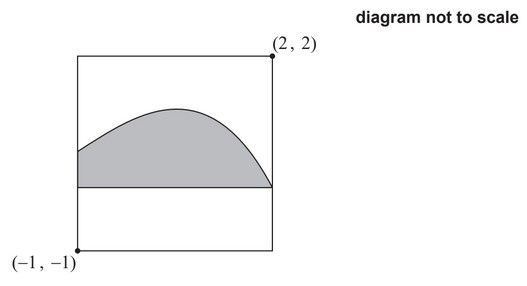
When the painting is placed on a coordinate axes such that the bottom left corner of the
painting has coordinates (−1, −1) and the top right corner has coordinates (2 , 2), the
curve can be modelled by y = f (x) and the horizontal line can be modelled by the x-axis.
Distances are measured in metres.
(a) Use the trapezoidal rule, with the values given in the following table, to approximate
the area of the shaded region.
| x | -1 | 0 | 1 | 2 |
| y | 0.6 | 1.2 | 1.2 | 0 |
The artist used the equation \(y=\frac{-x^3-3x^2+4x+12}{10}\) to draw the curve.
(b) Find the exact area of the shaded region in the painting.
(c) Find the area of the unshaded region in the painting.
Answer/Explanation
Ans:
(a) \(\frac{1}{2}(0.6+0+2(1.2 + 1.2))\)
2.7 \(m^2\)
(b) \(\int_{-1}^{2}\frac{-x^3-3x^2+4x+12}{10}\) OR \(\int_{-1}^{2}f(x)dx\)
2.925 \(m^2\)
(c) 9-2.925
= 6.08 \(m^2\) (6.075)
Question
A small manufacturing company makes and sells \(x\) machines each month. The monthly cost \(C\) , in dollars, of making \(x\) machines is given by
\[C(x) = 2600 + 0.4{x^2}{\text{.}}\]The monthly income \(I\) , in dollars, obtained by selling \(x\) machines is given by
\[I(x) = 150x – 0.6{x^2}{\text{.}}\]\(P(x)\) is the monthly profit obtained by selling \(x\) machines.
Find \(P(x)\) .[2]
Find the number of machines that should be made and sold each month to maximize \(P(x)\) .[2]
Use your answer to part (b) to find the selling price of each machine in order to maximize \(P(x)\) .[2]
Answer/Explanation
Markscheme
\(P(x) = I(x) – C(x)\) (M1)
\( = – {x^2} + 150x – 2600\) (A1) (C2)
\( – 2x + 150 = 0\) (M1)
Note: Award (M1) for setting \(P'(x) = 0\) .
OR
Award (M1) for sketch of \(P(x)\) and maximum point identified. (M1)
\(x = 75\) (A1)(ft) (C2)
Note: Follow through from their answer to part (a).
\(\frac{{7875}}{{75}}\) (M1)
Note: Award (M1) for \(7875\) seen.
\( = 105\) (A1)(ft) (C2)
Note: Follow through from their answer to part (b).
Question
[Maximum mark: 10]
The cost of producing a mathematics textbook is $ 15 and it is then sold for $ x .
(a) Find an expression for the profit made on each book sold. [1]
A total of (100 000 – 4000 x ) books is sold.
(b) Show that the profit made on all the books sold is P= 160000x-4000x2 -1500000 [3]
(c) (i) Find \(\frac{dP}{dx}\)
(ii) Hence calculate the value of x to make a maximum profit [4]
(d) Calculate the number of books sold to make this maximum profit. [2]
Answer/Explanation
Answer:
(a) x – 15
(b) Profit = (x – 15) (100 000 – 4000x)
= 100000x – 4000x2 – 1500 000 + 60 000x= 160 000x – 4000x2 – 1500 000
(c) (i) \(\frac{dP}{dx}=160000-8000x\)
(ii) 160000 – 8000x=0 ⇔ x =\(\frac{160000}{8000}\Leftrightarrow x=20\)
(d) Books sold = 100 000 – 4000 × 20 = 20000
