Question 16. [Maximum mark: 8]
A particle P moves in a straight line, such that its displacement x at time t (t ≥ 0) is defined by the differential equation x ̇ = x cost(e−sin t ).
At time t = 0 , x = \(\frac{1}{c}\) .
a. By using Euler’s method with a step length of 0.1, find an approximate value
for x when t = 0.3 . [3]
b. By solving the differential equation, find the percentage error in your approximation
for x when t = 0.3 . [5]
▶️Answer/Explanation
(a) \(x_{n}=x_{n-1}+h f(x_{n-1},t_{n-1}\)
\(h = 0.1\),\( f (x,t)= xcost (e^{-sint}\)
\(x_{n}=x_{n-1}+ 0.1x_{n-1} cost_{n-1}e^{-sint}\)
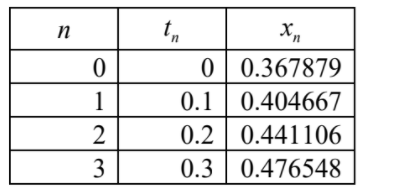
\(x (0.3) ≈ 0.477 (0.476548…)\)
(b) EITHER
\(\int \frac{dx}{x}= \int cost(e^{-sint})dt +c\)
\(ln x = e^{-sint}+ c\)
\(t= 0, x= \frac{1}{e}\Rightarrow c=0\)
\(x = e^{-sint}\)
\(x(0.3)=0.475\)
THEN percentage error \(= |\frac{0.476548.. – 0.475140..}{0.475140..}|\times 100\)
\(= 0.296%(2.96192..)\)
Question
A slope field for the differential equation \(\frac{dy}{dx}=x^2 + \frac{y}{2}\) is shown.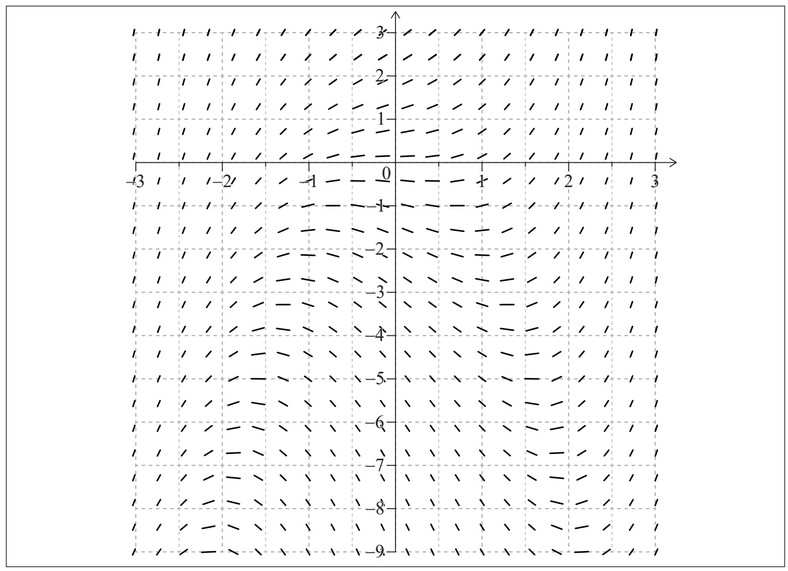
Some of the solutions to the differential equation have a local maximum point and a local
minimum point.
(a) (i) Write down the equation of the curve on which all these maximum and minimum points lie.
(ii) Sketch this curve on the slope field.
The solution to the differential equation that passes through the point (0 , −2) has both a
local maximum point and a local minimum point.
(b) On the slope field, sketch the solution to the differential equation that passes
through (0, −2).
▶️Answer/Explanation
Ans:
(a) (i) \(x^2+\frac{y}{2}=0 (y=-2x^2)\)
(ii) \(y=-2x^2\) drawn on diagram (correct shape with a maximum at (0, 0))
(b)
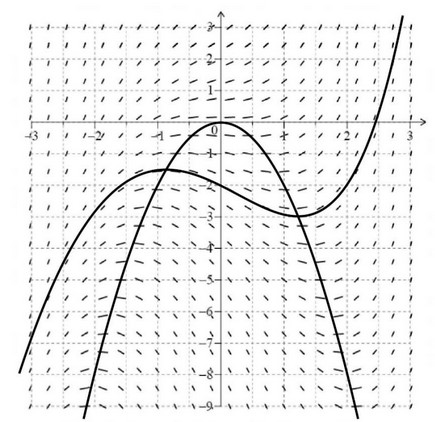
correct shape with a local maximum and minimum, passing through (0, 2)
local maximum and minimum on the graph of \(y=-2x^2\)
Question
Consider the differential equation \(\frac{{{\text{d}}y}}{{{\text{d}}x}} = {y^3} – {x^3}\) for which \(y = 1\) when \(x = 0\). Use Euler’s method with a step length of \(0.1\) to find an approximation for the value of \(y\) when \(x = 0.4\).
▶️Answer/Explanation
Markscheme
use of \(y \to y + h\frac{{{\text{d}}y}}{{{\text{d}}x}}\) (M1)
| \(x\) | \(y\) | \({\text{d}}y{\text{/d}}x\) | \(h{\text{d}}y{\text{/d}}x\) | |
| 0 | 1 | 1 | 0.1 | (A1) |
| 0.1 | 1.1 | 1.33 | 0.133 | A1 |
| 0.2 | 1.233 | 1.866516337 | 0.1866516337 | A1 |
| 0.3 | 1.419651634 | 2.834181181 | 0.283418118 | A1 |
| 0.4 | 1.703069752 | (A1) |
Note: After the first line, award A1 for each subsequent \(y\) value, provided it is correct to 3sf.
approximate value of \(y(0.4) = 1.70\) A1
Note: Accept \(1.7\) or any answers that round to \(1.70\).
[7 marks]
Question
▶️Answer/Explanation
Markscheme
\(\frac{{\text{d}}}{{{\text{d}}x}}({x^2}\tan y) = 2x\tan y + {x^2}{\sec ^2}y\frac{{{\text{d}}y}}{{{\text{d}}x}}\) M1A1A1
\({x^2}\frac{{{\text{d}}y}}{{{\text{d}}x}} + 2x\sin y\cos y = {x^3}{\cos ^2}y\) A1
\( \Rightarrow {x^2}{\sec ^2}y\frac{{{\text{d}}y}}{{{\text{d}}x}} + 2x\tan y = {x^3}\) M1A1
\( \Rightarrow \frac{{\text{d}}}{{{\text{d}}x}}({x^2}\tan y) = {x^3}\) A1
\({x^2}\tan y = \frac{{{x^4}}}{4} + c\) A1
Note: Condone the omission of \(c\) in the line above
when \(x = 1,{\text{ }}y = 0 \Rightarrow c = – \frac{1}{4}\) M1
\(\tan y = \frac{{{x^2}}}{4} – \frac{1}{{4{x^2}}}\)
\(y = \arctan \left( {\frac{{{x^2}}}{4} – \frac{1}{{4{x^2}}}} \right)\) A1
