IBDP Maths AHL 5.17 Area of the region and Volumes of revolution about the x-axis or y-axis AA HL Paper 1- New Syllabus

Step 1: Identify the integration formula
For a rotation about the \( y \)-axis, the volume \( V \) is given by the integral: [cite_start]\( V = \pi \int_{y_1}^{y_2} x^2 \, dy \)[cite: 1599].

Step 2: Determine the limits of integration
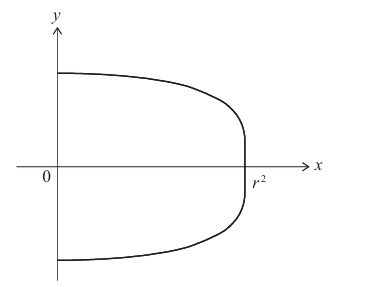
From the equation \( x^2 + y^4 = r^4 \), the curve intersects the \( y \)-axis when \( x = 0 \):
\( 0 + y^4 = r^4 \implies y = \pm r \).
The limits are from \( y = -r \) to \( y = r \).

Step 3: Set up and evaluate the integral
Express \( x^2 \) in terms of \( y \): \( x^2 = r^4 – y^4 \).
Due to the symmetry of the region across the \( x \)-axis, we can integrate from \( 0 \) to \( r \) and double the result:
\( V = 2\pi \int_{0}^{r} (r^4 – y^4) \, dy \).
Integrating with respect to \( y \):
\( V = 2\pi \left[ r^4y – \frac{y^5}{5} \right]_{0}^{r} \).
Substitute the limits:
\( V = 2\pi \left( (r^4 \cdot r – \frac{r^5}{5}) – (0) \right) \)
\( V = 2\pi \left( r^5 – \frac{1}{5}r^5 \right) = 2\pi \left( \frac{4}{5}r^5 \right) \).
\( V = \frac{8}{5}\pi r^5 \).

Final Answer:
\(\boxed{V = \frac{8}{5} \pi r^5}\)