IBDP Maths AHL 5.19Maclaurin series AA HL Paper 2- Exam Style Questions- New Syllabus
Assuming the Maclaurin series for \( \cos x \) and \( \ln(1+x) \), show that the Maclaurin series for \( \cos(\ln(1+x)) \) is:
\[1-\frac{1}{2}x^2+\frac{1}{2}x^{3}-\frac{5}{12}x^{4}+\cdots\] [4]
By differentiating the series in part (a), show that the Maclaurin series for \( \sin(\ln(1+x)) \) is:
\[x -\frac{1}{2}x^2+\frac{1}{6}x^{3}+\cdots\] [4]
Hence determine the Maclaurin series for \( \tan(\ln(1+x)) \) as far as the term in \( x^3 \). [5]
▶️ Answer/Explanation
(a) Maclaurin Series for \( \cos(\ln(1+x)) \):
METHOD 1:
M1: Substitutes \( \ln(1+x) = x – \frac{1}{2}x^2 + \frac{1}{3}x^3 – \frac{1}{4}x^4 +\cdots \) into \( \cos x = 1 – \frac{1}{2}x^2 + \frac{1}{24}x^4 -\cdots \)
M1: Expands up to \( x^4 \) terms:
\( \cos(\ln(1+x)) = 1 – \frac{1}{2}\left(x – \frac{1}{2}x^2 + \frac{1}{3}x^3\right)^2 + \frac{1}{24}x^4 +\cdots \)
A1: Correct expansion:
\( = 1 – \frac{1}{2}\left(x^2 – x^3 + \frac{11}{12}x^4\right) +\cdots \)
A1: Final result: \( \boxed{1-\frac{1}{2}x^2+\frac{1}{2}x^{3}-\frac{5}{12}x^{4}+\cdots} \)
METHOD 2:
M1: Uses \( \cos(\ln(1+x)) = 1 – \frac{1}{2}(\ln(1+x))^2 + \frac{1}{24}(\ln(1+x))^4 -\cdots \)
M1: Finds \( (\ln(1+x))^2 = x^2 – x^3 + \frac{11}{12}x^4 +\cdots \)
A1: Correct computation of terms
A1: Same final result as Method 1
(b) Maclaurin Series for \( \sin(\ln(1+x)) \):
M1: Differentiates part (a) result:
\( \frac{d}{dx}[\cos(\ln(1+x))] = -\sin(\ln(1+x)) \cdot \frac{1}{1+x} = -x + \frac{3}{2}x^2 – \frac{5}{3}x^3 +\cdots \)
M1: Solves for \( \sin(\ln(1+x)) \):
\( \sin(\ln(1+x)) = -(1+x)\left(-x + \frac{3}{2}x^2 – \frac{5}{3}x^3 +\cdots\right) \)
A1: Expands product:
\( = x – \frac{1}{2}x^2 + \frac{1}{6}x^3 +\cdots \)
A1: Final result: \( \boxed{x -\frac{1}{2}x^2+\frac{1}{6}x^{3}+\cdots} \)
(c) Maclaurin Series for \( \tan(\ln(1+x)) \):
METHOD 1:
M1: Sets \( \tan(\ln(1+x)) = \frac{\sin(\ln(1+x))}{\cos(\ln(1+x))} \)
M1: Writes denominator as \( \left(1 – \frac{1}{2}x^2 + \frac{1}{2}x^3\right)^{-1} \approx 1 + \frac{1}{2}x^2 – \frac{1}{2}x^3 +\cdots \)
M1: Multiplies series:
\( \left(x – \frac{1}{2}x^2 + \frac{1}{6}x^3\right)\left(1 + \frac{1}{2}x^2 – \frac{1}{2}x^3\right) \)
A1: Correct expansion:
\( = x – \frac{1}{2}x^2 + \frac{2}{3}x^3 +\cdots \)
A1: Final result: \( \boxed{x -\frac{1}{2}x^2+\frac{2}{3}x^{3}+\cdots} \)
METHOD 2: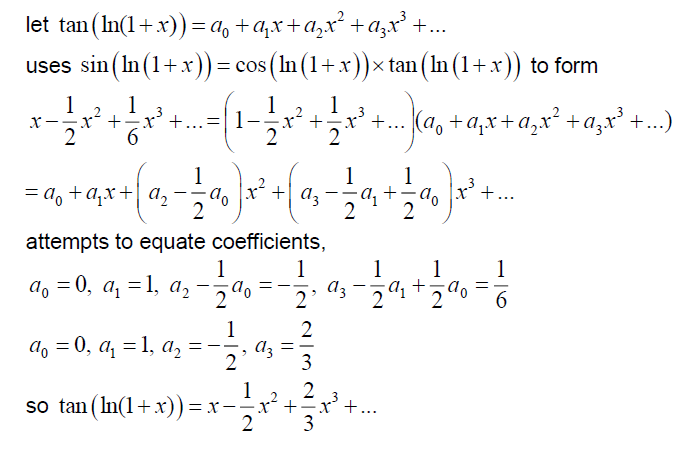
(a) Write down the first three terms of the binomial expansion of \( (1 + t)^{-1} \) in ascending powers of \( t \). [1]
(b) By using the Maclaurin series for \( \cos x \) and the result from part (a), show that the Maclaurin series for \( \sec x \) up to and including the term in \( x^4 \) is:
\[ \boxed{1 + \frac{x^2}{2} + \frac{5x^4}{24}} \] [4]
(c) By using the Maclaurin series for \( \arctan x \) and the result from part (b), find:
\[ \lim_{x\to 0} \frac{x \arctan(2x)}{\sec x – 1} \] [3]
▶️ Answer/Explanation
(a) Binomial Expansion:
\[ (1 + t)^{-1} = 1 – t + t^2 – t^3 + \cdots \] First three terms: \(\boxed{1 – t + t^2}\)
(b) Maclaurin Series for \(\sec x\):
Starting with: \[ \cos x = 1 – \frac{x^2}{2!} + \frac{x^4}{4!} – \cdots = 1 – \frac{x^2}{2} + \frac{x^4}{24} – \cdots \] Using the binomial expansion: \[ \sec x = \left(1 – \frac{x^2}{2} + \frac{x^4}{24}\right)^{-1} \approx 1 + \left(\frac{x^2}{2} – \frac{x^4}{24}\right) + \left(\frac{x^2}{2}\right)^2 \] Combining terms: \[ = 1 + \frac{x^2}{2} – \frac{x^4}{24} + \frac{x^4}{4} = \boxed{1 + \frac{x^2}{2} + \frac{5x^4}{24}} \]
(c) Limit Calculation:
Using series expansions: \[ \arctan(2x) = 2x – \frac{(2x)^3}{3} + \cdots = 2x – \frac{8x^3}{3} + \cdots \] \[ \sec x – 1 \approx \frac{x^2}{2} + \frac{5x^4}{24} \] The limit becomes: \[ \lim_{x\to 0} \frac{x\left(2x – \frac{8x^3}{3}\right)}{\frac{x^2}{2} + \frac{5x^4}{24}} = \lim_{x\to 0} \frac{2x^2 – \frac{8x^4}{3}}{\frac{x^2}{2} + \frac{5x^4}{24}} \] Dividing numerator and denominator by \(x^2\): \[ = \lim_{x\to 0} \frac{2 – \frac{8x^2}{3}}{\frac{1}{2} + \frac{5x^2}{24}} = \frac{2}{\frac{1}{2}} = \boxed{4} \]
