Question
The sum of the first 16 terms of an arithmetic sequence is 212 and the fifth term is 8.
a.Find the first term and the common difference.[4]
b.Find the smallest value of n such that the sum of the first n terms is greater than 600.[3]
▶️Answer/Explanation
Markscheme
\({S_n} = \frac{n}{2}[2a + (n – 1)d]\)
\(212 = \frac{{16}}{2}(2a + 15d)\,\,\,\,\,( = 16a + 120d)\) A1
\({n^{th}}{\text{ term is }}a + (n – 1)d\)
\(8 = a + 4d\) A1
solving simultaneously: (M1)
\(d = 1.5,{\text{ }}a = 2\) A1
[4 marks]
\(\frac{n}{2}[4 + 1.5(n – 1)] > 600\) (M1)
\( \Rightarrow 3{n^2} + 5n – 2400 > 0\) (A1)
\( \Rightarrow n > 27.4…,{\text{ }}(n < – 29.1…)\)
Note: Do not penalize improper use of inequalities.
\( \Rightarrow n = 28\) A1
[3 marks]
Examiners report
This proved to be a good start to the paper for most candidates. The vast majority made a meaningful attempt at this question with many gaining the correct answers. Candidates who lost marks usually did so because of mistakes in the working. In part (b) the most efficient way of gaining the answer was to use the calculator once the initial inequality was set up. A small number of candidates spent valuable time unnecessarily manipulating the algebra before moving to the calculator.
This proved to be a good start to the paper for most candidates. The vast majority made a meaningful attempt at this question with many gaining the correct answers. Candidates who lost marks usually did so because of mistakes in the working. In part (b) the most efficient way of gaining the answer was to use the calculator once the initial inequality was set up. A small number of candidates spent valuable time unnecessarily manipulating the algebra before moving to the calculator.
Question
Each time a ball bounces, it reaches 95 % of the height reached on the previous bounce.
Initially, it is dropped from a height of 4 metres.
a.What height does the ball reach after its fourth bounce?[2]
b.How many times does the ball bounce before it no longer reaches a height of 1 metre?[3]
c.What is the total distance travelled by the ball?[3]
▶️Answer/Explanation
Markscheme
height \( = 4 \times {0.95^4}\) (A1)
= 3.26 (metres) A1
[2 marks]
\(4 \times {0.95^n} < 1\) (M1)
\({0.95^n} < 0.25\)
\( \Rightarrow n > \frac{{\ln 0.25}}{{\ln 0.95}}\) (A1)
\( \Rightarrow n > 27.0\)
Note: Do not penalize improper use of inequalities.
\( \Rightarrow n = 28\) A1
Note: If candidates have used n – 1 rather than n throughout penalise in part (a) and treat as follow through in parts (b) and (c).
[3 marks]
METHOD 1
recognition of geometric series with sum to infinity, first term of \(4 \times 0.95\) and common ratio 0.95 M1
recognition of the need to double this series and to add 4 M1
total distance travelled is \(2\left( {\frac{{4 \times 0.95}}{{1 – 0.95}}} \right) + 4 = 156{\text{ (metres)}}\) A1
[3 marks]
Note: If candidates have used n – 1 rather than n throughout penalise in part (a) and treat as follow through in parts (b) and (c).
METHOD 2
recognition of a geometric series with sum to infinity, first term of 4 and common ratio 0.95 M1
recognition of the need to double this series and to subtract 4 M1
total distance travelled is \({\text{2}}\left( {\frac{4}{{1 – 0.95}}} \right) – 4 = 156{\text{ (metres)}}\) A1
[3 marks]
Question
Find the sum of all the multiples of 3 between 100 and 500.
▶️Answer/Explanation
Markscheme
METHOD 1
102 + 105 + … + 498 (M1)
so number of terms = 133 (A1)
EITHER
\( = \frac{{133}}{2}(2 \times 102 + 132 \times 3)\) (M1)
= 39900 A1
OR
\( = (102 + 498) \times \frac{{133}}{2}\) (M1)
= 39900 A1
OR
\(\sum\limits_{n = 34}^{166} {3n} \) (M1)
= 39900 A1
METHOD 2
\(500 \div 3 = 166.666…{\text{ and }}100 \div 3 = 33.333…\)
\(102 + 105 + … + 498 = \sum\limits_{n = 1}^{166} {3n} – \sum\limits_{n = 1}^{33} {3n} \) (M1)
\(\sum\limits_{n = 1}^{166} {3n} = 41583\) (A1)
\(\sum\limits_{n = 1}^{33} {3n} = 1683\) (A1)
the sum is 39900 A1
[4 marks]
Examiners report
Most candidates got full marks in this question. Some mistakes were detected when trying to find the number of terms of the arithmetic sequence, namely the use of the incorrect value n = 132 ; a few interpreted the question as the sum of multiples between the 100th and 500th terms. Occasional application of geometric series was attempted.
Question
A metal rod 1 metre long is cut into 10 pieces, the lengths of which form a geometric sequence. The length of the longest piece is 8 times the length of the shortest piece. Find, to the nearest millimetre, the length of the shortest piece.
▶️Answer/Explanation
Markscheme
the pieces have lengths \(a,{\text{ }}ar,{\text{ …, }}a{r^9}\) (M1)
\(8a = a{r^9}{\text{ }}({\text{or }}8 = {r^9})\) A1
\(r = \sqrt[9]{8} = 1.259922…\) A1
\(a\frac{{{r^{10}} – 1}}{{r – 1}} = 1\,\,\,\,\,\left( {{\text{or }}a\frac{{{r^{10}} – 1}}{{r – 1}} = 1000} \right)\) M1
\(a = \frac{{r – 1}}{{{r^{10}} – 1}} = 0.0286…\,\,\,\,\,\left( {{\text{or }}a = \frac{{r – 1}}{{{r^{10}} – 1}} = 28.6…} \right)\) (A1)
a = 29 mm (accept 0.029 m or any correct answer regardless the units) A1
[6 marks]
Examiners report
This question was generally well done by most candidates. Some candidates recurred to a diagram to comprehend the nature of the problem but a few thought it was an arithmetic sequence.
A surprising number of candidates missed earning the final A1 mark because they did not read the question instructions fully and missed the accuracy instruction to give the answer correct to the nearest mm.
Question
A geometric sequence has a first term of 2 and a common ratio of 1.05. Find the value of the smallest term which is greater than 500.
▶️Answer/Explanation
Markscheme
\(2 \times {1.05^{n – 1}} > 500\) M1
\(n – 1 > \frac{{\log {\text{ }}250}}{{\log {\text{ }}1.05}}\) M1
\(n – 1 > 113.1675…\) A1
\(n = 115\) (A1)
\({u_{115}} = 521\) A1 N5
Note: Accept graphical solution with appropriate sketch.
[5 marks]
Examiners report
Many candidates misread the question and stopped at showing that the required term was the \({115^{{\text{th}}}}\).
Question
A geometric sequence has a first term of 2 and a common ratio of 1.05.
Find the value of the smallest term that is greater than 500.
▶️Answer/Explanation
Ans
2 × 1.05n–1 > 500 so 1.05n–1 > 250
METHOD A: Trial and error;
The smallest integer that satisfies the inequality is n = 115
METHOD B: Graphical solution by sketching an appropriate graph (GDC)
The smallest integer that satisfies the inequality is n = 115
METHOD C: Using logarithms;
\(n=1>\frac{log250}{log1.02}\)
\(n-1>113.1675…\) so n = 115
Then u115 = 521
Question
The diagram shows a sector AOB of a circle of radius 1 and centre O, where AOB = θ The lines (AB1), (A1B2), (A2B3) are perpendicular to OB. A1B1, A2B2 are all arcs of circles with centre O.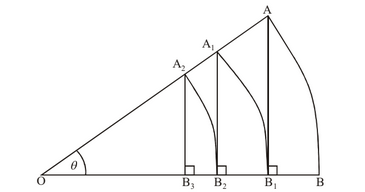
Calculate the sum to infinity of the arc lengths AB + A1B1 + A2B2 + A3B3 + ….
▶️Answer/Explanation
Ans
Arc AB = θ
OB1 = cosθ
Arc A1B1 = θcosθ
Similarly,
Arc A2B2 = θcos2θ
Sum = θ + θcosθ + θcos2θ + ….
=\(\frac {\theta}{1-cos\theta }\)
