IBDP MAA SL 1.5: Laws of exponents with integer HL Paper 1- Exam Questions
Question
(ii) Describe the sequence of transformations required to map the graph of \( y = g^{-1}(x) \) onto the graph of \( y = f(x) \).
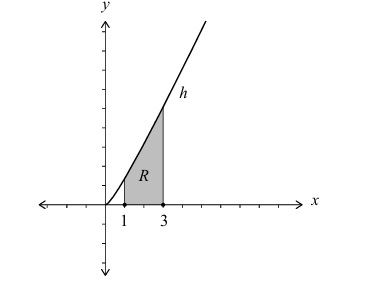
(ii) Hence, calculate the exact area of region \( R \) in the form \( p + q \ln r \), where \( p, q, r \in \mathbb{Q}^+ \).
Syllabus Topic Codes (IB Mathematics AA HL):
• SL 2.2: Concept of a function, domain, range and inverse function — parts (a), (b)(i)
• SL 2.5: Composite functions; Finding the inverse function — parts (b)(i), (c)
• SL 2.11: Transformations of graphs — part (b)(ii)
• SL 5.5: Introduction to integration; definite integrals and area — part (d)(ii)
• SL 5.10: Indefinite integral of \( \frac{1}{x} \); integration by substitution — part (d)(ii)
▶️ Answer/Explanation
(a)
We solve \( 4^x = 8 \).
Write \( 4 = 2^2 \) and \( 8 = 2^3 \): \( (2^2)^x = 2^3 \) → \( 2^{2x} = 2^3 \) → \( 2x = 3 \) → \( x = \frac32 \).
Thus \( f^{-1}(8) = \frac32 \).
\( \boxed{\frac{3}{2}} \)
(b)(i)
Let \( y = g^{-1}(x) \). Then \( g(y) = x \) ⇒ \( 1 + \log_2 y = x \) ⇒ \( \log_2 y = x – 1 \) ⇒ \( y = 2^{x-1} \).
So \( g^{-1}(x) = 2^{x-1} \).
\( \boxed{g^{-1}(x) = 2^{x-1}} \)
(b)(ii)
We have \( g^{-1}(x) = 2^{x-1} \) and \( f(x) = 4^x = 2^{2x} \).
To transform \( y = 2^{x-1} \) into \( y = 2^{2x} \):
1. Horizontal stretch with scale factor \( \frac12 \) (or compression by factor 2) changes \( x \) to \( 2x \): \( y = 2^{2x-1} \).
2. Then vertical stretch with scale factor 2 (or multiply by 2) changes \( 2^{2x-1} \) to \( 2^{2x} \).
Equivalently, a horizontal translation 1 unit left gives \( y = 2^x \), then horizontal stretch with scale factor \( \frac12 \) gives \( y = 2^{2x} \).
Horizontal stretch scale factor \( \frac12 \), then vertical stretch scale factor 2 (order can vary if both are independent stretches).
(c)
\( (f \circ g)(x) = f(g(x)) = 4^{g(x)} = 4^{1 + \log_2 x} \).
Since \( 4 = 2^2 \), \( 4^{1 + \log_2 x} = 2^{2(1+\log_2 x)} = 2^{2 + 2\log_2 x} = 2^2 \cdot 2^{2\log_2 x} = 4 \cdot (2^{\log_2 x})^2 = 4x^2 \).
\( \boxed{(f \circ g)(x) = 4x^2} \)
(d)(i)
Start with the right side: \( \dfrac{4x^2}{2x+1} \).
Rewrite numerator: \( 4x^2 = (2x+1)(2x-1) + 1 \).
Then \( \dfrac{4x^2}{2x+1} = \dfrac{(2x+1)(2x-1)+1}{2x+1} = 2x-1 + \dfrac{1}{2x+1} \).
(d)(ii)
Area \( R = \displaystyle \int_{1}^{3} h(x) \, dx = \int_{1}^{3} \left( 2x – 1 + \frac{1}{2x+1} \right) dx \).
Integrate termwise: \( \displaystyle \int (2x-1) \, dx = x^2 – x \), and \( \displaystyle \int \frac{1}{2x+1} \, dx = \frac12 \ln|2x+1| \).
Thus \( \left[ x^2 – x + \frac12 \ln(2x+1) \right]_{1}^{3} \).
Evaluate: \( \bigl( 9 – 3 + \frac12 \ln 7 \bigr) – \bigl( 1 – 1 + \frac12 \ln 3 \bigr) = 6 + \frac12 \ln 7 – \frac12 \ln 3 = 6 + \frac12 \ln \frac{7}{3} \).
\( \boxed{6 + \frac{1}{2} \ln \frac{7}{3}} \)