Question
The following diagram shows the graph of y = arctan( \(2x+1+\frac{\pi}{4} \)) for \(x \in \mathbb{R}\) with asymptotes at \(y=-\frac{\pi}{4}\) and \(y=\frac{3\pi}{4}\)
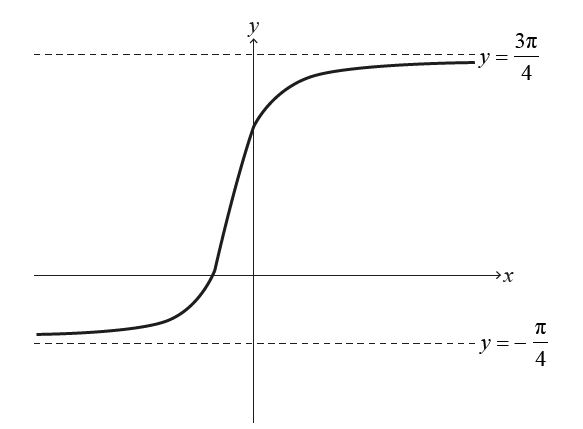
(a) Describe a sequence of transformations that transforms the graph of y = arctan x to the graph of y = arctan( \(2x+1+\frac{\pi}{4} \)) for \(x \in \mathbb{R}\) [3]
(b) Show that arctan arctan p+ arctan q= arctan \(\frac{p+q}{1-pq}\) where p , q > 0 and pq < 1 [4]
(c) Verify that \(arctan(2x+1) = arctan(\frac{x}{x+1})+\frac{\pi}{4}\) for x ∈ \(\mathbb{R}\) , x > 0 . [3]
(d) Using mathematical induction and the result from part (b), prove that
\(\sum_{r=1}^{n}arctan\frac{1}{2r^2}=arctan\frac{n}{n+1}\) for n ∈ \(\mathbb{Z}^+\)
▶️Answer/Explanation
Ans:
(a) By replacing the $x$ in $y=\arctan x$ with $x+1$, we obtain $y=\arctan \left(x+1\right)$, which is a translation of $-1$ units parallel to the $x$-axis.
Next, by replacing the $x$ in $y=\arctan \left(x+1\right)$ with $2x$, we obtain $y=\arctan \left(2x+1\right)$, which is a stretch parallel to the $x$-axis by scale factor $\frac{1}{2}$.
Finally, by replacing the $y$ in $y=\arctan \left(2x+1\right)$ with $y-\frac{\pi}{4}$, we obtain $y-\frac{\pi}{4}=\arctan \left(2x+1\right)$, i.e., $y=\arctan \left(2x+1\right)+\frac{\pi}{4}$, which is a translation of $\frac{\pi}{4}$ units parallel to the $y$-axis.<br>
(b) Taking tangent on both sides in $\arctan p+\arctan q=\arctan\left(\frac{p+q}{1-pq}\right)$, we have $\tan\left(\arctan p+\arctan q\right)=\frac{p+q}{1-pq}$
$$\begin{eqnarray}
\text{LHS} &=& \tan\left(\arctan p+\arctan q\right) \nonumber \\
&=& \frac{p+q}{1-pq} \nonumber \\
&=& \text{RHS}.
\end{eqnarray}$$
(c) Observe that $\arctan 1=\frac{\pi}{4}$. Then, using (b), we have
$$\begin{eqnarray}
\text{RHS} &=& \arctan \left(\frac{x}{x+1}\right)+\frac{\pi}{4} \nonumber \\
&=& \arctan \left(\frac{x}{x+1}\right)+\arctan 1 \nonumber \\
&=& \arctan \left(\frac{1+\frac{x}{x+1}}{1-\frac{x}{x+1}}\right) \nonumber \\
&=& \arctan \left(\frac{2x+1}{x+1-x}\right) \nonumber \\
&=& \arctan \left(2x+1\right) \nonumber \\
&=& \text{LHS}.
\end{eqnarray}$$
(d) Let $\text{P}_n$ be the proposition “$\sum_{r=1}^{n} \arctan\left(\frac{1}{2r^2}\right)=\arctan\left(\frac{n}{n+1}\right)$” for $n\in\mathbb{Z}^+$.<br>
When $n=1$,<br>
$$\begin{eqnarray}
\text{LHS}=\sum_{r=1}^{1} \arctan\left(\frac{1}{2r^2}\right)=\arctan\left(\frac{1}{2}\right) \nonumber \\
\text{RHS}=\arctan\left(\frac{1}{1+1}\right)=\arctan\left(\frac{1}{2}\right).
\end{eqnarray}$$
Since $\text{LHS}=\text{RHS}$, $\text{P}_1$ is true.<br>
Assume that $\text{P}_k$ is true for some $k\in\mathbb{Z}^+$, i.e.,
$$\begin{eqnarray}
\sum_{r=1}^{k} \arctan\left(\frac{1}{2r^2}\right)=\arctan\left(\frac{k}{k+1}\right).
\end{eqnarray}$$
To show that $\text{P}_{k+1}$ is also true, i.e.,
$$\begin{eqnarray}
\sum_{r=1}^{k+1} \arctan\left(\frac{1}{2r^2}\right)=\arctan\left(\frac{k+1}{k+2}\right).
\end{eqnarray}$$
$$\begin{eqnarray}
\text{LHS} &=& \sum_{r=1}^{k+1} \arctan\left(\frac{1}{2r^2}\right) \nonumber \\
&=& \arctan\left(\frac{k}{k+1}\right)+\arctan\left(\frac{1}{2\left(k+1\right)^2}\right) \nonumber \\
&=& \arctan \left[\frac{\frac{k}{k+1}+\frac{1}{2\left(k+1\right)^2}}{1-\frac{k}{2\left(k+1\right)^3}}\right] \nonumber \\
&=& \arctan \left[\frac{2k\left(k+1\right)^2+\left(k+1\right)}{2\left(k+1\right)^3-k}\right] \nonumber \\
&=& \arctan \left[\frac{\left(k+1\right)\left(2k^2+2k+1\right)}{\left(k+2\right)\left(2k^2+2k+1\right)}\right] \nonumber \\
&=& \arctan \left(\frac{k+1}{k+2}\right) \nonumber \\
&=& \text{RHS}.
\end{eqnarray}$$
Since $\text{P}_1$ is true and $\text{P}_k$ is true implies $\text{P}_{k+1}$ is also true, by the principle of mathematical induction, $\text{P}_n$ is true for $n\in\mathbb{Z}^+$.
Question
(a) Express the quadratic \(3{x^2} – 6x + 5\) in the form \(a{(x + b)^2} + c\), where a, b, c \( \in \mathbb{Z}\).
(b) Describe a sequence of transformations that transforms the graph of \(y = {x^2}\) to the graph of \(y = 3{x^2} – 6x + 5\).
▶️Answer/Explanation
Markscheme
(a) attempt at completing the square (M1)
\(3{x^2} – 6x + 5 = 3({x^2} – 2x) + 5 = 3{(x – 1)^2} – 1 + 5\) (A1)
\( = 3{(x – 1)^2} + 2\) A1
\((a = 3,{\text{ }}b = – 1,{\text{ }}c = 2)\)
(b) definition of suitable basic transformations:
\({{\text{T}}_1} = \) stretch in y direction scale factor 3 A1
\({{\text{T}}_2} = \) translation \(\left( {\begin{array}{*{20}{c}}
1 \\
0
\end{array}} \right)\) A1
\({{\text{T}}_3} = \) translation \(\left( {\begin{array}{*{20}{c}}
0 \\
2
\end{array}} \right)\) A1
[6 marks]
Question
The quadratic function \(f(x) = p + qx – {x^2}\) has a maximum value of 5 when x = 3.
Find the value of p and the value of q .[4]
The graph of f(x) is translated 3 units in the positive direction parallel to the x-axis. Determine the equation of the new graph.[2]
▶️Answer/Explanation
Markscheme
METHOD 1
\(f'(x) = q – 2x = 0\) M1
\(f'(3) = q – 6 = 0\)
q = 6 A1
f(3) = p + 18 − 9 = 5 M1
p = −4 A1
METHOD 2
\(f(x) = – {(x – 3)^2} + 5\) M1A1
\( = – {x^2} + 6x – 4\)
q = 6, p = −4 A1A1
[4 marks]
\(g(x) = – 4 + 6(x – 3) – {(x – 3)^2}{\text{ }}( = – 31 + 12x – {x^2})\) M1A1
Note: Accept any alternative form which is correct.
Award M1A0 for a substitution of (x + 3) .
[2 marks]
Question
Let \(f(x) = {x^3} + a{x^2} + bx + c\) , where a , b , \(c \in \mathbb{Z}\) . The diagram shows the graph of y = f(x) .
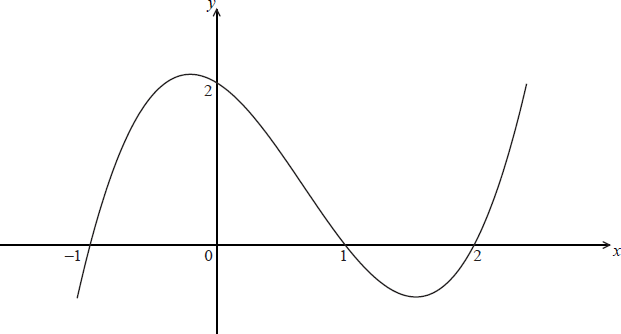
Using the information shown in the diagram, find the values of a , b and c .[4]
If g(x) = 3f(x − 2) ,
(i) state the coordinates of the points where the graph of g intercepts the x-axis.
(ii) Find the y-intercept of the graph of g .[3]
▶️Answer/Explanation
Markscheme
METHOD 1
f(x) = (x + 1)(x − 1)(x − 2) M1
\( = {x^3} – 2{x^2} – x + 2\) A1A1A1
a = −2 , b = −1 and c = 2
METHOD 2
from the graph or using f(0) = 2
c = 2 A1
setting up linear equations using f(1) = 0 and f(–1) = 0 (or f(2) = 0) M1
obtain a = −2 , b = −1 A1A1
[4 marks]
(i) (1, 0) , (3, 0) and (4, 0) A1
(ii) g(0) occurs at 3f(−2) (M1)
= −36 A1
[3 marks]
Question: [Maximum mark: 7]
Consider f (x) = 4sinx + 2.5 and \(g(x) = 4sin\left ( x-\frac{3\pi }{2} \right )+ 2.5 + q,\) where x ∈ R and q > 0. The graph of g is obtained by two transformations of the graph of f .
(a) Describe these two transformations.
The y-intercept of the graph of g is at (0, r).
(b) Given that g(x) ≥ 7, find the smallest value of r.
▶️Answer/Explanation
Ans:
(a) translation (shift) by \(\frac{3\pi }{2}\) to the right OR positive horizontal direction by \(\frac{3\pi }{2}\)
translation (shift) by q upwards OR positive vertical direction by q
Note: accept translation by \(\binom{\frac{3\pi }{2}}{q}\)
Do not accept ‘move’ for translation/shift.
(b)
minimum of \(\left ( x-\frac{3\pi }{2} \right )\) is -4 (may be seen in sketch)
-4 + 2.5 + q ≥7
q≥ 8.5 (accept q = 8.5)
substituting x = 0 and their q (= 8.5) to find r
(r =) \(4sin\left ( \frac{-3\pi }{2} \right )+2.5 + 8.5\)
4 + 2.5 + 8.5
smallest value of r is 15
