Question
a.In triangle \(ABC\),
\(3\sin B + 4\cos C = 6\) and
\(4\sin C + 3\cos B = 1\).
Show that \(\sin (B + C) = \frac{1}{2}\).[6]
b.Robert conjectures that \({\rm{C\hat AB}}\) can have two possible values.
Show that Robert’s conjecture is incorrect by proving that \({\rm{C\hat AB}}\) has only one possible value.[5]
▶️Answer/Explanation
Markscheme
METHOD 1
squaring both equations M1
\(9{\sin ^2}B + 24\sin B\cos C + 16{\cos ^2}C = 36\) (A1)
\(9{\cos ^2}B + 24\cos B\sin C + 16{\sin ^2}C = 1\) (A1)
adding the equations and using \({\cos ^2}\theta + {\sin ^2}\theta = 1\) to obtain \(9 + 24\sin (B + C) + 16 = 37\) M1
\(24(\sin B\cos C + \cos B\sin C) = 12\) A1
\(24\sin (B + C) = 12\) (A1)
\(\sin (B + C) = \frac{1}{2}\) AG
METHOD 2
substituting for \(\sin B\) and \(\cos B\) to obtain
\(\sin (B + C) = \left( {\frac{{6 – 4\cos C}}{3}} \right)\cos C + \left( {\frac{{1 – 4\sin C}}{3}} \right)\sin C\) M1
\( = \frac{{6\cos C + \sin C – 4}}{3}\;\;\;\)(or equivalent) A1
substituting for \(\sin C\) and \(\cos C\) to obtain
\(\sin (B + C) = \sin B\left( {\frac{{6 – 3\sin B}}{4}} \right) + \cos B\left( {\frac{{1 – 3\cos B}}{4}} \right)\) M1
\( = \frac{{\cos B + 6\sin B – 3}}{4}\;\;\;\)(or equivalent) A1
Adding the two equations for \(\sin (B + C)\):
\(2\sin (B + C) = \frac{{(18\sin B + 24\cos C) + (4\sin C + 3\cos B) – 25}}{{12}}\) A1
\(\sin (B + C) = \frac{{36 + 1 – 25}}{{24}}\) (A1)
\(\sin (B + C) = \frac{1}{2}\) AG
METHOD 3
substituting \(\sin B\) and \(\sin C\) to obtain
\(\sin (B + C) = \left( {\frac{{6 – 4\cos C}}{3}} \right)\cos C + \cos B\left( {\frac{{1 – 3\cos B}}{4}} \right)\) M1
substituting for \(\cos B\) and \(\cos B\) to obtain
\(\sin (B + C) = \sin B\left( {\frac{{6 – 3\sin B}}{4}} \right) + \left( {\frac{{1 – 4\sin C}}{3}} \right)\sin C\) M1
Adding the two equations for \(\sin (B + C)\):
\(2\sin (B + C) = \frac{{6\cos C + \sin C – 4}}{3} + \frac{{6\sin B + \cos B – 3}}{4}\;\;\;\)(or equivalent) A1A1
\(2\sin (B + C) = \frac{{(18\sin B + 24\cos C) + (4\sin C + 3\cos B) – 25}}{{12}}\) A1
\(\sin (B + C) = \frac{{36 + 1 – 25}}{{24}}\) (A1)
\(\sin (B + C) = \frac{1}{2}\) AG
[6 marks]
\(\sin A = \sin \left( {180^\circ – (B + C)} \right)\) so \(\sin A = \sin (B + C)\) R1
\(\sin (B + C) = \frac{1}{2} \Rightarrow \sin A = \frac{1}{2}\) A1
\( \Rightarrow A = 30^\circ \) or \(A = 150^\circ \) A1
if \(A = 150^\circ \), then \(B < 30^\circ \) R1
for example, \(3\sin B + 4\cos C < \frac{3}{2} + 4 < 6\), ie a contradiction R1
only one possible value \((A = 30^\circ )\) AG
[5 marks]
Total [11 marks]
Examiners report
Most candidates found this a difficult question with a large number of candidates either not attempting it or making little to no progress. In part (a), most successful candidates squared both equations, added them together, used \({\cos ^2}\theta + {\sin ^2}\theta = 1\) and then simplified their result to show that \(\sin (B + C) = \frac{1}{2}\). A number of candidates started with a correct alternative method (see the markscheme for alternative approaches) but were unable to follow them through fully.
In part (b), a small percentage of candidates were able to obtain \(B + C = 30^\circ {\text{ }}(A = 150^\circ )\) or \(B + C = 150^\circ {\text{ }}(A = 30^\circ )\) but were then unable to demonstrate or explain why \(A = 30^\circ \) is the only possible value for triangle ABC.
Question
Let \(z = r(\cos \alpha + {\text{i}}\sin \alpha )\), where \(\alpha \) is measured in degrees, be the solution of \({z^5} – 1 = 0\) which has the smallest positive argument.
a. (i) Use the binomial theorem to expand \({(\cos \theta + {\text{i}}\sin \theta )^5}\).
(ii) Hence use De Moivre’s theorem to prove
\[\sin 5\theta = 5{\cos ^4}\theta \sin \theta – 10{\cos ^2}\theta {\sin ^3}\theta + {\sin ^5}\theta .\]
(iii) State a similar expression for \(\cos 5\theta \) in terms of \(\cos \theta \) and \(\sin \theta \).[6]
b.Find the value of \(r\) and the value of \(\alpha \).[4]
c.Using (a) (ii) and your answer from (b) show that \(16{\sin ^4}\alpha – 20{\sin ^2}\alpha + 5 = 0\).[4]
d.Hence express \(\sin 72^\circ \) in the form \(\frac{{\sqrt {a + b\sqrt c } }}{d}\) where \(a,{\text{ }}b,{\text{ }}c,{\text{ }}d \in \mathbb{Z}\).[5]
▶️Answer/Explanation
Markscheme
(i) \({(\cos \theta + {\text{i}}\sin \theta )^5}\)
\( = {\cos ^5}\theta + 5{\text{i}}{\cos ^4}\theta \sin \theta + 10{{\text{i}}^2}{\cos ^3}\theta {\sin ^2}\theta + \)
\(10{{\text{i}}^3}{\cos ^2}\theta {\sin ^3}\theta + 5{{\text{i}}^4}\cos \theta {\sin ^4}\theta + {{\text{i}}^5}{\sin ^5}\theta \) A1A1
\(( = {\cos ^5}\theta + 5{\text{i}}{\cos ^4}\theta \sin \theta – 10{\cos ^3}\theta {\sin ^2}\theta – \)
\(10{\text{i}}{\cos ^2}\theta {\sin ^3}\theta + 5\cos \theta {\sin ^4}\theta + {\text{i}}{\sin ^5}\theta )\)
Note: Award first A1 for correct binomial coefficients.
(ii) \({({\text{cis}}\theta )^5} = {\text{cis}}5\theta = \cos 5\theta + {\text{i}}\sin 5\theta \) M1
\( = {\cos ^5}\theta + 5{\text{i}}{\cos ^4}\theta \sin \theta – 10{\cos ^3}\theta {\sin ^2}\theta – 10{\text{i}}{\cos ^2}\theta {\sin ^3}\theta + \)
\(5\cos \theta {\sin ^4}\theta + {\text{i}}{\sin ^5}\theta \) A1
Note: Previous line may be seen in (i)
equating imaginary terms M1
\(\sin 5\theta = 5{\cos ^4}\theta \sin \theta – 10{\cos ^2}\theta {\sin ^3}\theta + {\sin ^5}\theta \) AG
(iii) equating real terms
\(\cos 5\theta = {\cos ^5}\theta – 10{\cos ^3}\theta {\sin ^2}\theta + 5\cos \theta {\sin ^4}\theta \) A1
[6 marks]
\({(r{\text{cis}}\alpha )^5} = 1 \Rightarrow {r^5}{\text{cis}}5\alpha = 1{\text{cis}}0\) M1
\({r^5} = 1 \Rightarrow r = 1\) A1
\(5\alpha = 0 \pm 360k,{\text{ }}k \in \mathbb{Z} \Rightarrow a = 72k\) (M1)
\(\alpha = 72^\circ \) A1
Note: Award M1A0 if final answer is given in radians.
[4 marks]
use of \(\sin (5 \times 72) = 0\) OR the imaginary part of \(1\) is \(0\) (M1)
\(0 = 5{\cos ^4}\alpha \sin \alpha – 10{\cos ^2}\alpha {\sin ^3}\alpha + {\sin ^5}\alpha \) A1
\(\sin \alpha \ne 0 \Rightarrow 0 = 5{(1 – {\sin ^2}\alpha )^2} – 10(1 – {\sin ^2}\alpha ){\sin ^2}\alpha + {\sin ^4}\alpha \) M1
Note: Award M1 for replacing \({\cos ^2}\alpha \).
\(0 = 5(1 – 2{\sin ^2}\alpha + {\sin ^4}\alpha ) – 10{\sin ^2}\alpha + 10{\sin ^4}\alpha + {\sin ^4}\alpha \) A1
Note: Award A1 for any correct simplification.
so \(16{\sin ^4}\alpha – 20{\sin ^2}\alpha + 5 = 0\) AG
[4 marks]
\({\sin ^2}\alpha = \frac{{20 \pm \sqrt {400 – 320} }}{{32}}\) M1A1
\(\sin \alpha = \pm \sqrt {\frac{{20 \pm \sqrt {80} }}{{32}}} \)
\(\sin \alpha = \frac{{ \pm \sqrt {10 \pm 2\sqrt 5 } }}{4}\) A1
Note: Award A1 regardless of signs. Accept equivalent forms with integral denominator, simplification may be seen later.
as \(72 > 60\), \(\sin 72 > \frac{{\sqrt 3 }}{2} = 0.866 \ldots \) we have to take both positive signs (or equivalent argument) R1
Note: Allow verification of correct signs with calculator if clearly stated
\(\sin 72 = \frac{{\sqrt {10 + 2\sqrt 5 } }}{4}\) A1
[5 marks]
Total [19 marks]
Examiners report
In part (i) many candidates tried to multiply it out the binomials rather than using the binomial theorem. In parts (ii) and (iii) many candidates showed poor understanding of complex numbers and made no attempt to equate real and imaginary parts. In a some cases the correct answer to part (iii) was seen although it was unclear how it was obtained.
This question was poorly done. Very few candidates made a good attempt to apply De Moivre’s theorem and most of them could not even equate the moduli to obtain \(r\).
This question was poorly done. From the few candidates that attempted it, many candidates started by writing down what they were trying to prove and made no progress.
Very few made a serious attempt to answer this question. Also very few realised that they could use the answers given in part (c) to attempt this part.
Question
Points A , B and T lie on a line on an indoor soccer field. The goal, [AB] , is 2 metres wide. A player situated at point P kicks a ball at the goal. [PT] is perpendicular to (AB) and is 6 metres from a parallel line through the centre of [AB] . Let PT be \(x\) metros and let \(\alpha = {\rm{A\hat PB}}\) measured in degrees. Assume that the ball travels along the floor.
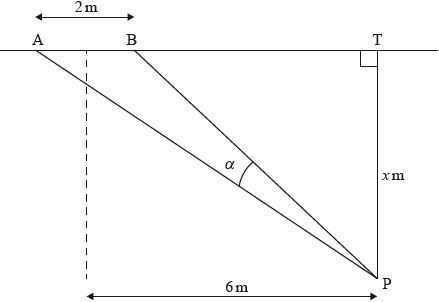
The maximum for \(\tan \alpha \) gives the maximum for \(\alpha \).
Find the value of \(\alpha \) when \(x = 10\).
Show that \(\tan \alpha = \frac{{2x}}{{{x^2} + 35}}\).
(i) Find \(\frac{{\text{d}}}{{{\text{d}}x}}(\tan \alpha )\).
(ii) Hence or otherwise find the value of \(\alpha \) such that \(\frac{{\text{d}}}{{{\text{d}}x}}(\tan \alpha ) = 0\).
(iii) Find \(\frac{{{{\text{d}}^2}}}{{{\text{d}}{x^2}}}(\tan \alpha )\) and hence show that the value of \(\alpha \) never exceeds 10°.
Find the set of values of \(x\) for which \(\alpha \geqslant 7^\circ \).
▶️Answer/Explanation
Markscheme
EITHER
\(\alpha = \arctan \frac{7}{{10}} – \arctan \frac{5}{{10}}{\text{ }}( = 34.992 \ldots ^\circ – 26.5651 \ldots ^\circ )\) (M1)(A1)(A1)
Note: Award (M1) for \(\alpha = {\rm{A\hat PT}} – {\rm{B\hat PT}}\), (A1) for a correct \({\rm{A\hat PT}}\) and (A1) for a correct \({\rm{B\hat PT}}\).
OR
\(\alpha = \arctan {\text{ }}2 – \arctan \frac{{10}}{7}{\text{ }}( = 63.434 \ldots ^\circ – 55.008 \ldots ^\circ )\) (M1)(A1)(A1)
Note: Award (M1) for \(\alpha = {\rm{P\hat BT}} – {\rm{P\hat AT}}\), (A1) for a correct \({\rm{P\hat BT}}\) and (A1) for a correct \({\rm{P\hat AT}}\).
OR
\(\alpha = \arccos \left( {\frac{{125 + 149 – 4}}{{2 \times \sqrt {125} \times \sqrt {149} }}} \right)\) (M1)(A1)(A1)
Note: Award (M1) for use of cosine rule, (A1) for a correct numerator and (A1) for a correct denominator.
THEN
\( = 8.43^\circ \) A1
[4 marks]
EITHER
\(\tan \alpha = \frac{{\frac{7}{x} – \frac{5}{x}}}{{1 + \left( {\frac{7}{x}} \right)\left( {\frac{5}{x}} \right)}}\) M1A1A1
Note: Award M1 for use of \(\tan (A – B)\), A1 for a correct numerator and A1 for a correct denominator.
\( = \frac{{\frac{2}{x}}}{{1 + \frac{{35}}{{{x^2}}}}}\) M1
OR
\(\tan \alpha = \frac{{\frac{x}{5} – \frac{x}{7}}}{{1 + \left( {\frac{x}{5}} \right)\left( {\frac{x}{7}} \right)}}\) M1A1A1
Note: Award M1 for use of xxx, A1 for a correct numerator and A1 for a correct denominator.
\( = \frac{{\frac{{2x}}{{35}}}}{{1 + \frac{{{x^2}}}{{35}}}}\) M1
OR
\(\cos \alpha = \frac{{{x^2} + 35}}{{\sqrt {({x^2} + 25)({x^2} + 49)} }}\) M1A1
Note: Award M1 for either use of the cosine rule or use of \(\cos (A – B)\).
\(\sin \alpha \frac{{2x}}{{\sqrt {({x^2} + 25)({x^2} + 49)} }}\) A1
\(\tan \alpha = \frac{{\frac{{2x}}{{\sqrt {({x^2} + 25)({x^2} + 49)} }}}}{{\frac{{{x^2} + 35}}{{\sqrt {({x^2} + 25)({x^2} + 49)} }}}}\) M1
THEN
\(\tan \alpha = \frac{{2x}}{{{x^2} + 35}}\) AG
[4 marks]
(i) \(\frac{{\text{d}}}{{{\text{d}}x}}(\tan \alpha ) = \frac{{2({x^2} + 35) – (2x)(2x)}}{{{{({x^2} + 35)}^2}}}{\text{ }}\left( { = \frac{{70 – 2{x^2}}}{{{{({x^2} + 35)}^2}}}} \right)\) M1A1A1
Note: Award M1 for attempting product or quotient rule differentiation, A1 for a correct numerator and A1 for a correct denominator.
(ii) METHOD 1
EITHER
\(\frac{{\text{d}}}{{{\text{d}}x}}(\tan \alpha ) = 0 \Rightarrow 70 – 2{x^2} = 0\) (M1)
\(x = \sqrt {35} {\text{ (m) }}\left( { = 5.9161 \ldots {\text{ (m)}}} \right)\) A1
\(\tan \alpha = \frac{1}{{\sqrt {35} }}{\text{ }}( = 0.16903 \ldots )\) (A1)
OR
attempting to locate the stationary point on the graph of
\(\tan \alpha = \frac{{2x}}{{{x^2} + 35}}\) (M1)
\(x = 5.9161 \ldots {\text{ (m) }}\left( { = \sqrt {35} {\text{ (m)}}} \right)\) A1
\(\tan \alpha = 0.16903 \ldots {\text{ }}\left( { = \frac{1}{{\sqrt {35} }}} \right)\) (A1)
THEN
\(\alpha = 9.59^\circ \) A1
METHOD 2
EITHER
\(\alpha = \arctan \left( {\frac{{2x}}{{{x^2} + 35}}} \right) \Rightarrow \frac{{{\text{d}}\alpha }}{{{\text{d}}x}} = \frac{{70 – 2{x^2}}}{{{{({x^2} + 35)}^2} + 4{x^2}}}\) M1
\(\frac{{{\text{d}}\alpha }}{{{\text{d}}x}} = 0 \Rightarrow x = \sqrt {35} {\text{ (m) }}\left( { = 5.9161{\text{ (m)}}} \right)\) A1
OR
attempting to locate the stationary point on the graph of
\(\alpha = \arctan \left( {\frac{{2x}}{{{x^2} + 35}}} \right)\) (M1)
\(x = 5.9161 \ldots {\text{ (m) }}\left( { = \sqrt {35} {\text{ (m)}}} \right)\) A1
THEN
\(\alpha = 0.1674 \ldots {\text{ }}\left( { = \arctan \frac{1}{{\sqrt {35} }}} \right)\) (A1)
\( = 9.59^\circ \) A1
(iii) \(\frac{{{{\text{d}}^2}}}{{{\text{d}}{x^2}}}(\tan \alpha ) = \frac{{{{({x^2} + 25)}^2}( – 4x) – (2)(2x)({x^2} + 35)(70 – 2{x^2})}}{{{{({x^2} + 35)}^4}}}{\text{ }}\left( { = \frac{{4x({x^2} – 105)}}{{{{({x^2} + 35)}^3}}}} \right)\) M1A1
substituting \(x = \sqrt {35} {\text{ }}( = 5.9161 \ldots )\) into \(\frac{{{{\text{d}}^2}}}{{{\text{d}}{x^2}}}(\tan \alpha )\) M1
\(\frac{{{{\text{d}}^2}}}{{{\text{d}}{x^2}}}(\tan \alpha ) < 0{\text{ }}( =- 0.004829 \ldots )\) and so \(\alpha = 9.59^\circ \) is the maximum value of \(\alpha \) R1
\(\alpha \) never exceeds 10° AG
[11 marks]
attempting to solve \(\frac{{2x}}{{{x^2} + 35}} \geqslant \tan 7^\circ \) (M1)
Note: Award (M1) for attempting to solve \(\frac{{2x}}{{{x^2} + 35}} = \tan 7^\circ \).
\(x = 2.55\) and \(x = 13.7\) (A1)
\(2.55 \leqslant x \leqslant 13.7{\text{ (m)}}\) A1
[3 marks]
Examiners report
This question was generally accessible to a large majority of candidates. It was pleasing to see a number of different (and quite clever) trigonometric methods successfully employed to answer part (a) and part (b).
This question was generally accessible to a large majority of candidates. It was pleasing to see a number of different (and quite clever) trigonometric methods successfully employed to answer part (a) and part (b).
The early parts of part (c) were generally well done. In part (c) (i), a few candidates correctly found \(\frac{{\text{d}}}{{{\text{d}}x}}(\tan \alpha )\) in unsimplified form but then committed an algebraic error when endeavouring to simplify further. A few candidates merely stated that \(\frac{{\text{d}}}{{{\text{d}}x}}(\tan \alpha ) = {\sec ^2}\alpha \).
Part (c) (ii) was reasonably well done with a large number of candidates understanding what was required to find the correct value of \(\alpha \) in degrees. In part (c)(iii), a reasonable number of candidates were able to successfully find \(\frac{{{{\text{d}}^2}}}{{{\text{d}}{x^2}}}(\tan \alpha )\) in unsimplified form. Some however attempted to solve \(\frac{{{{\text{d}}^2}}}{{{\text{d}}{x^2}}}(\tan \alpha ) = 0\) for \(\chi \) rather than examine the value of \(\frac{{{{\text{d}}^2}}}{{{\text{d}}{x^2}}}(\tan \alpha )\) at \(x = \sqrt {35} \).
Part (d), which required use of a GCD to determine an inequality, was surprisingly often omitted by candidates. Of the candidates who attempted this part, a number stated that \(x \geqslant 2.55\). Quite a sizeable proportion of candidates who obtained the correct inequality did not express their answer to 3 significant figures.
Question
Let \(f\left( x \right) = {\text{tan}}\left( {x + \pi } \right){\text{cos}}\left( {x – \frac{\pi }{2}} \right)\) where \(0 < x < \frac{\pi }{2}\).
Express \(f\left( x \right)\) in terms of sin \(x\) and cos \(x\).
▶️Answer/Explanation
Markscheme
\({\text{tan}}\left( {x + \pi } \right) = \tan x\left( { = \frac{{{\text{sin}}\,x}}{{{\text{cos}}\,x}}} \right)\) (M1)A1
\({\text{cos}}\left( {x – \frac{\pi }{2}} \right) = {\text{sin}}\,x\) (M1)A1
Note: The two M1s can be awarded for observation or for expanding.
\({\text{tan}}\left( {x + \pi } \right) = {\text{cos}}\left( {x – \frac{\pi }{2}} \right) = \frac{{{\text{si}}{{\text{n}}^2}\,x}}{{{\text{cos}}\,x}}\) A1
[5 marks]
