Question
A company manufactures metal tubes for bicycle frames. The diameters of the tubes, Dmm, are normally distributed with mean 32 and standard deviation s. The interquartile range of the diameters is 0.28.
Find the value of \(\sigma \).
▶️Answer/Explanation
Answer:
METHOD 1
\(Q_1\) = 31.86 OR \(Q_3\) = 32.14 recognition that the area under the normal curve below \(Q_1\) or above \(Q_3\) is 0.25 OR the area between \(Q_1\) and \(Q_3\) is 0.5 (seen anywhere including on a diagram)
EITHER
equating an appropriate correct normal CDF function to its correct probability (0.25 or 0.5 or 0.75)
OR
z = −0.674489… OR z = 0.674489… (seen anywhere)
-0.674489… = \(\frac{31.86 – 32}{\sigma }\) OR 0.674489… = \(\frac{32.14 – 32}{\sigma }\)
THEN
0.207564…
\(\sigma = 0.208\) (mm)
METHOD 2
recognition that the area under the normal curve below \(Q_1\) or above \(Q_3\) is 0.25 OR the area between \(Q_1\) and \(Q_3\) is 0.5 (seen anywhere including on a diagram)
z = −0.674489… OR z = 0.674489…
\((Q_1=) 32 – 0.674489… \sigma \) OR \((Q_3 =) 32 + 0.674489… \sigma \)
\((Q_3 – Q_1 =) 2 \times 0.674489… \sigma \)
2 \(\times \) 0.674489… \(\sigma \) = 0.28
0.207564…
\(\sigma = 0.208\) (mm)
The interquartile range (IQR) is a measure of statistical dispersion, which is the difference between the third quartile (Q3) and the first quartile (Q1) of a dataset. For a normal distribution, the IQR is related to the standard deviation \((\sigma)\) by a factor of approximately 1.35.
\(\text{IQR} = Q_3 – Q_1 = 1.349\sigma\)
Where:
- IQR is the interquartile range
- Q3 is the 75th percentile
- Q1 is the 25th percentile
- σ is the standard deviation
The interquartile range of the diameters is 0.28.
We can substitute the known IQR value into the equation: \(0.28 = 1.349\sigma \)
\(\sigma = \frac{0.28}{1.349} \)
\(\sigma \approx 0.208\)
Question
A survey at a swimming pool is given to one adult in each family. The age of the adult, a years old, and of their eldest child, c years old, are recorded.
The ages of the eldest child are summarized in the following box and whisker diagram.
diagram not to scale

(a) Find the largest value of c that would not be considered an outlier.
The regression line of a on c is \(a = \frac{7}{4}c + 20.\) The regression line of c on a is \(c = \frac{1}{2}a – 9.\)
(b) (i) One of the adults surveyed is 42 years old. Estimate the age of their eldest child.
(ii) Find the mean age of all the adults surveyed.
▶️Answer/Explanation
Ans:
(a) IQR = 10 – 6 (=4)
attempt to find Q3 + 1.5 × IQR
10 + 6
16
(b)
(i) choosing c = \(\frac{1}{2}a – 9\)
\(\frac{1}{2}\times 42-9\)
= 12 (years old)
(ii) attempt to solve system by substitution or elimination
34 (years old)
Question
A research student weighed lizard eggs in grams and recorded the results. The following box and whisker diagram shows a summary of the results where L and U are the lower and upper quartiles respectively.
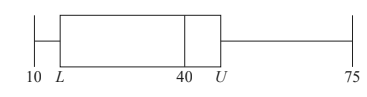
diagram not to scale
The interquartile range is 20 grams and there are no outliers in the results.
(a) Find the minimum possible value of U . [3]
(b) Hence, find the minimum possible value of L . [2]
▶️Answer/Explanation
Ans:

Question
A scientist has 100 female fish and 100 male fish. She measures their lengths to the nearest cm. These are shown in the following box and whisker diagrams.
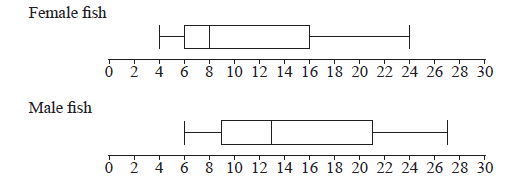
a.Find the range of the lengths of all 200 fish.[3]
Four cumulative frequency graphs are shown below.
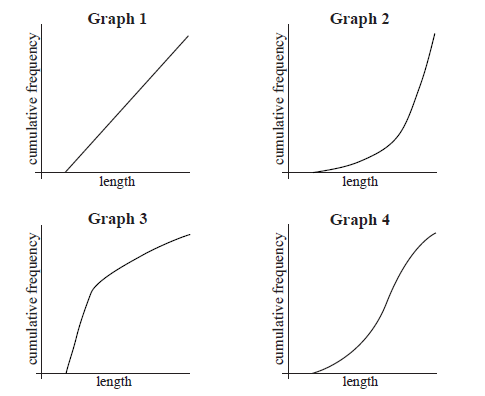
Which graph is the best representation of the lengths of the female fish?[2]
▶️Answer/Explanation
Markscheme
a.correct end points (A1)(A1)
max = 27 , min = 4
range = 23 A1 N3
[3 marks]
Graph 3 A2 N2
[2 marks]
Question
The weekly wages (in dollars) of 80 employees are displayed in the cumulative frequency curve below.
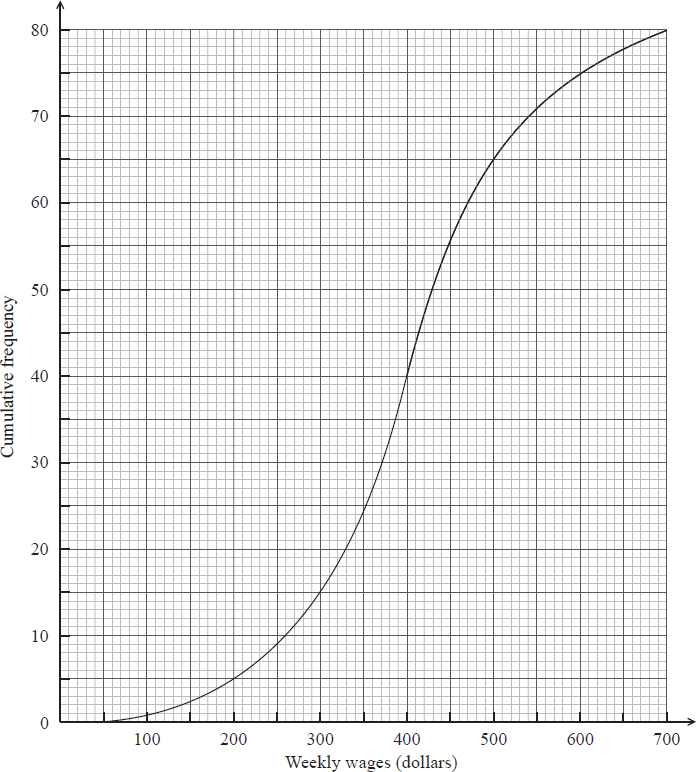
(i) Write down the median weekly wage.
(ii) Find the interquartile range of the weekly wages.[4]
The box-and-whisker plot below displays the weekly wages of the employees.
Write down the value of
(i) \(a\) ;
(ii) \(b\) ;
(iii) \(c\) .[3]
b(i), (ii), (iii). c.Find the median number of hours worked per week.[3]
d.Employees are paid \(\$ 20\) per hour.
Find the number of employees who work more than \(25\) hours per week.[5]
▶️Answer/Explanation
Markscheme
a(i) and (ii).(i) median weekly wage \(= 400\) (dollars) A1 N1
(ii) lower quartile \(= 330\), upper quartile \(= 470\) (A1)(A1)
\({\text{IQR}} = 140\) (dollars) (accept any notation suggesting interval \(330\) to \(470\)) A1 N3
Note: Exception to the FT rule. Award A1(FT) for an incorrect IQR only if both quartiles are explicitly noted.
[4 marks]
(i) \(330\) (dollars) A1 N1
(ii) \(400\) (dollars) A1 N1
(iii) \(700\) (dollars) A1 N1
[3 marks]
valid approach (M1)
e.g. \({\rm{hours = }}\frac{{{\rm{wages}}}}{{{\rm{rate}}}}\)
correct substitution (A1)
e.g. \(\frac{{400}}{{20}}\)
median hours per week \(= 20\) A1 N2
[3 marks]
attempt to find wages for 25 hours per week (M1)
e.g. \({\text{wages}} = {\text{hours}} \times {\text{rate}}\)
correct substitution (A1)
e.g. \(25 \times 20\)
finding wages \(= 500\) (A1)
65 people (earn 500\( \leqslant \)) (A1)
15 people (work more than 25 hours) A1 N3
[5 marks]
Question
The following box-and-whisker plot shows the number of text messages sent by students in a school on a particular day.
a.Find the value of the interquartile range.[2]
b.One student sent k text messages, where k > 11 . Given that k is an outlier, find the least value of k.[4]
▶️Answer/Explanation
Markscheme
a. recognizing Q1 or Q3 (seen anywhere) (M1)
eg 4,11 , indicated on diagram
IQR = 7 A1 N2
[2 marks]
recognizing the need to find 1.5 IQR (M1)
eg 1.5 × IQR, 1.5 × 7
valid approach to find k (M1)
eg 10.5 + 11, 1.5 × IQR + Q3
21.5 (A1)
k = 22 A1 N3
Note: If no working shown, award N2 for an answer of 21.5.
[4 marks]
