IB Mathematics AA AHL Integration by substitution Study Notes - New Syllabus

IB Mathematics AA AHL Informal ideas of limit, continuity and convergence Study Notes

LEARNING OBJECTIVE

Integration by substitution.

Key Concepts:

Integration by substitution.
Integration by parts

When to Use Substitution

Use substitution when the integrand contains a composition of functions of the form $ f(g(x)) \cdot g'(x) $. This is essentially reversing the chain rule from differentiation.

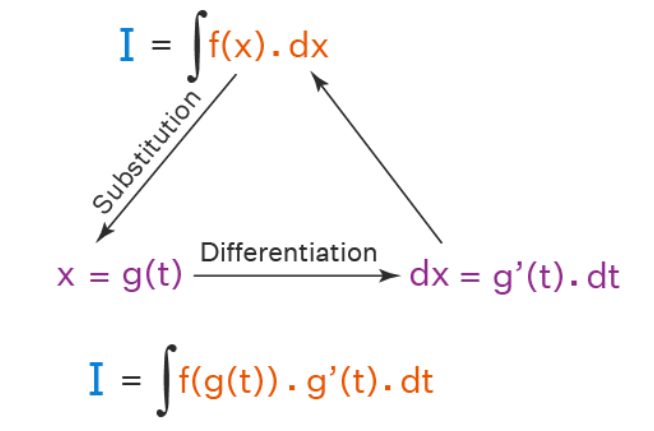
Substitution Method

Let $ u = g(x) $, so that $ \frac{du}{dx} = g'(x) \Rightarrow dx = \frac{du}{g'(x)} $. Substitute into the integral and simplify.

General Rule

$\boxed{ \int f(g(x))g'(x)\, dx = \int f(u)\, du = F(u) + C = F(g(x)) + C} $

Example 1

Evaluate $ \int 2x \cos(x^2 + 1)\, dx $

▶️ Answer/Explanation

Solution:

Let $ u = x^2 + 1 \Rightarrow \frac{du}{dx} = 2x \Rightarrow dx = \frac{du}{2x} $

Now substitute:

$ \int 2x \cos(u) \cdot \frac{du}{2x} = \int \cos(u)\, du $

$ = \sin(u) + C $

Substitute back $ u = x^2 + 1 $:

Final Answer: $ \sin(x^2 + 1) + C $

Example 2

Evaluate $ \int_{1}^{3} \frac{2x}{x^2 + 1}\, dx $

▶️ Answer/Explanation

Solution:

Let $ u = x^2 + 1 \Rightarrow du = 2x\, dx $

Change limits: When $ x = 1 $, $ u = 2 $; when $ x = 3 $, $ u = 10 $

Then:

$ \int_{1}^{3} \frac{2x}{x^2 + 1}\, dx = \int_{2}^{10} \frac{1}{u}\, du = \ln|u| \Big|_{2}^{10} $

Final Answer: $ \ln(10) – \ln(2) = \ln\left(\frac{10}{2}\right) = \ln(5) $

Tips:

Choose a substitution that simplifies the integrand to a basic function.
Always express $ dx $ in terms of $ du $.
For definite integrals, change the limits of integration.

When to Use Integration by Parts

Use integration by parts when the integral is a product of two functions where direct integration is difficult. It is based on reversing the product rule of differentiation.

Integration by Parts Formula

$\boxed{ \int u \, dv = uv – \int v \, du }$

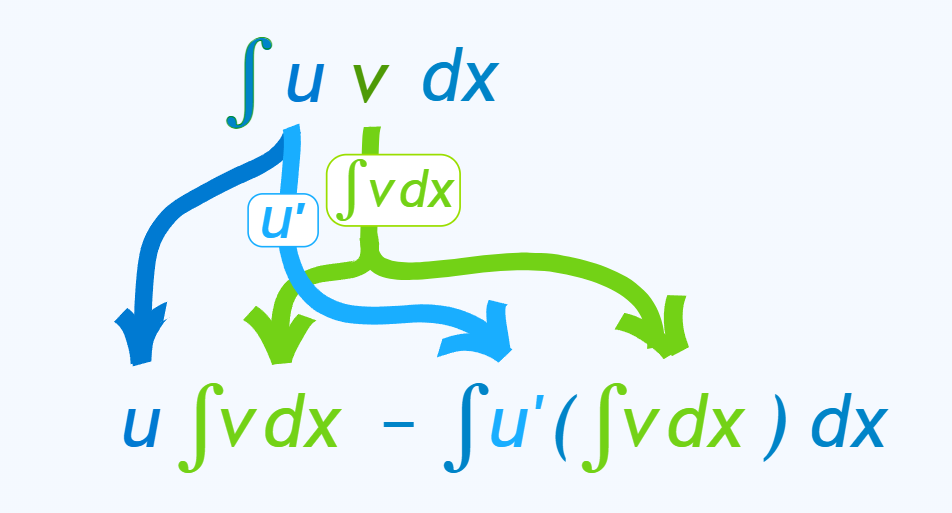
Method

1. Choose $ u = $ function to differentiate and $ dv = $ function to integrate.
2. Compute $ du = \frac{du}{dx} dx $ and $ v = \int dv $.
3. Substitute into the formula $ \int u\, dv = uv – \int v\, du $.
4. Evaluate the remaining integral and add $ + C $ for indefinite integrals.

Example 1

Evaluate $ \int x \sin x \, dx $

▶️ Answer/Explanation

Solution:

Let $ u = x $ so that $ du = dx $.

Let $ dv = \sin x \, dx $, so $ v = -\cos x $.

Apply the formula:

$ \int x \sin x \, dx = uv – \int v\, du = -x \cos x + \int \cos x \, dx $ $ = -x \cos x + \sin x + C $

Example 2

Evaluate $ \int \ln x \, dx $

▶️ Answer/Explanation

Solution:

Let $ u = \ln x $, so $ du = \frac{1}{x} dx $.

Let $ dv = dx $, so $ v = x $.

Apply the formula:

$ \int \ln x \, dx = uv – \int v\, du = x \ln x – \int x \cdot \frac{1}{x} dx = x \ln x – \int 1 \, dx $ $ = x \ln x – x + C $

Example 3

Evaluate $ \int \arcsin x \, dx $

▶️ Answer/Explanation

Solution:

Let $ u = \arcsin x $, so $ du = \frac{1}{\sqrt{1 – x^2}} dx $.

Let $ dv = dx $, so $ v = x $.

Apply the formula:

$ \int \arcsin x \, dx = uv – \int v\, du = x \arcsin x – \int \frac{x}{\sqrt{1 – x^2}} dx $

For the integral, use substitution $ t = 1 – x^2 $ or recall:

$ \int \frac{x}{\sqrt{1 – x^2}} dx = -\sqrt{1 – x^2} + C $

Thus,

$ \int \arcsin x \, dx = x \arcsin x + \sqrt{1 – x^2} + C $

Tips:

Choose $ u $ so that $ du $ simplifies the integral.
$ dv $ should be easily integrable.
Label each part clearly to avoid confusion.

Repeated Integration by Parts

Sometimes, applying integration by parts once is not enough. We may need to apply it multiple times, especially when integrating products like polynomials times exponentials or trigonometric functions.

Strategy:

Apply integration by parts repeatedly until the integral simplifies.
For cyclic integrals (like $ \int e^x \sin x\, dx $), you may need to solve for the integral algebraically after repeating.

Example 1: Evaluate $ \int x^2 e^x \, dx $

▶️ Answer/Explanation

Let $ u = x^2 \Rightarrow du = 2x \, dx $

Let $ dv = e^x dx \Rightarrow v = e^x $

Use integration by parts:

$ \int x^2 e^x \, dx = x^2 e^x – \int 2x e^x \, dx $

Now evaluate $ \int 2x e^x \, dx $ using integration by parts again:

Let $ u = 2x \Rightarrow du = 2 dx $

Let $ dv = e^x dx \Rightarrow v = e^x $

$ \int 2x e^x \, dx = 2x e^x – \int 2 e^x \, dx = 2x e^x – 2 e^x + C $

$ \int x^2 e^x \, dx = x^2 e^x – \left( 2x e^x – 2 e^x \right) + C = e^x (x^2 – 2x + 2) + C $

Example 2: Evaluate $ \int e^x \sin x \, dx $

▶️ Answer/Explanation

Let $ u = \sin x \Rightarrow du = \cos x \, dx $

Let $ dv = e^x dx \Rightarrow v = e^x $

Apply integration by parts:

$ \int e^x \sin x \, dx = e^x \sin x – \int e^x \cos x \, dx $

Evaluate $ \int e^x \cos x \, dx $ similarly:

Let $ u = \cos x \Rightarrow du = -\sin x \, dx $

Let $ dv = e^x dx \Rightarrow v = e^x $

$ \int e^x \cos x \, dx = e^x \cos x – \int e^x (-\sin x) \, dx = e^x \cos x + \int e^x \sin x \, dx $

$ \int e^x \sin x \, dx = e^x \sin x – \left( e^x \cos x + \int e^x \sin x \, dx \right) $ $ \int e^x \sin x \, dx = e^x \sin x – e^x \cos x – \int e^x \sin x \, dx $

$ 2 \int e^x \sin x \, dx = e^x ( \sin x – \cos x ) $ $ \int e^x \sin x \, dx = \frac{e^x}{2} ( \sin x – \cos x ) + C $

Previous Topic Notes

Next Topic Notes

IB Mathematics AA AHL Integration by substitution Study Notes

IB Mathematics AA AHL Integration by substitution Study Notes - New Syllabus

IB Mathematics AA AHL Informal ideas of limit, continuity and convergence Study Notes

Integration by Substitution

Integration by Parts

Repeated Integration by Parts

Resources

Members

Company