IB Mathematics AA HL Polar Forms Euler's Form Study Notes
IB Mathematics AA HL Polar Forms Euler’s Form Study Notes
IB Mathematics AA HL Polar Forms Euler’s Form Study Notes Offer a clear explanation of Polar Forms Euler’s Form , including various formula, rules, exam style questions as example to explain the topics. Worked Out examples and common problem types provided here will be sufficient to cover for topic Polar Forms Euler’s Form.
Modulus–Argument (Polar) Form
Modulus–Argument (Polar) Form
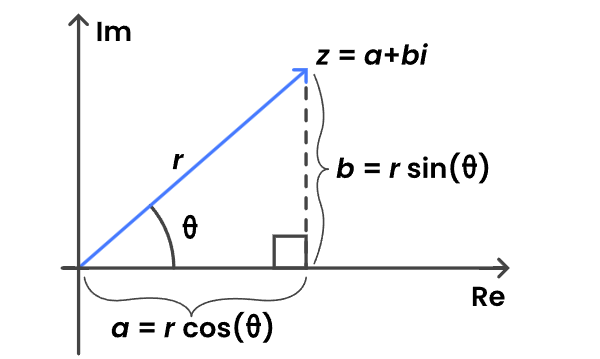
A complex number \( z = a + bi \) can also be expressed in polar form as:
\( z = r(\cos \theta + i\sin \theta) \)
Key Definitions
Modulus (r): The distance from the origin to the point:
\( r = |z| = \sqrt{a^2 + b^2} \)
Argument (θ): The angle with the positive real axis:
\( \theta = \tan^{-1}\left(\frac{b}{a}\right) \)
Notation: \( z = r \text{cis} \theta \) is shorthand for \( z = r(\cos \theta + i \sin \theta) \)
Note: The value of \( \theta \) depends on the quadrant in which the complex number lies.
Examples
- Convert \( z = 4 + 3i \) to polar form.
- Convert \( z = -2 – 5i \) to polar form.
▶️ Answer/Explanation
1.\( z = 4 + 3i \):
- Modulus: \( r = \sqrt{4^2 + 3^2} = \sqrt{16 + 9} = \sqrt{25} = 5 \)
- Argument: \( \theta = \tan^{-1}\left(\frac{3}{4}\right) \approx 0.644 \, \text{rad} \)
- Polar form: \( z = 5(\cos 0.644 + i\sin 0.644) \)
2.\( z = -2 – 5i \):
- Modulus: \( r = \sqrt{(-2)^2 + (-5)^2} = \sqrt{4 + 25} = \sqrt{29} \approx 5.385 \)
- Argument: \( \theta = \tan^{-1}\left(\frac{-5}{-2}\right) = \tan^{-1}(2.5) \approx 1.190 \, \text{rad} \)
- But since it’s in quadrant III, add \( \pi \):
\( \theta \approx 1.190 + \pi \approx 4.332 \, \text{rad} \) - Polar form: \( z \approx 5.385(\cos 4.332 + i\sin 4.332) \)
Euler Form of Complex Numbers
Euler Form of Complex Numbers
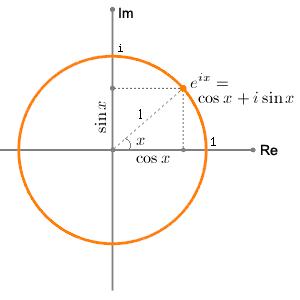
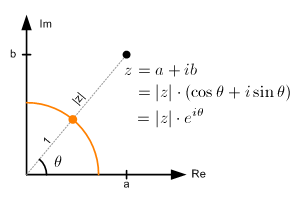
The Euler form of a complex number is a compact way to write it using exponential notation:
\( z = re^{i\theta} \)
Key Concepts
| Concept | Formula |
|---|---|
| Euler’s Formula | \( e^{i\theta} = \cos \theta + i\sin \theta \) |
| Modulus (r) | \( r = |z| = \sqrt{a^2 + b^2} \) |
| Argument (θ) | \( \theta = \arg(z) = \tan^{-1}\left(\frac{b}{a}\right) \) |
| Euler Form | \( z = re^{i\theta} \) |
This is simply the polar form written using Euler’s identity, and it’s especially useful for multiplication, division, and powers/roots of complex numbers.
Why Euler Form?
| Operation | Formula |
|---|---|
| Multiplication | \( z_1 z_2 = r_1 r_2 e^{i(\theta_1 + \theta_2)} \) |
| Division | \( \frac{z_1}{z_2} = \frac{r_1}{r_2} e^{i(\theta_1 – \theta_2)} \) |
| Powers | \( z^n = r^n e^{in\theta} \) |
| Roots | \( \sqrt[n]{z} = \sqrt[n]{r} \cdot e^{i(\frac{\theta + 2k\pi}{n})} \), where \( k = 0, 1, \ldots, n-1 \) |
Examples
- Express \( z = 4 + 4i \) in Euler form.
- Find the cube of \( z = 2e^{i\frac{\pi}{4}} \)
▶️Answer/Explanation
1. \( z = 4 + 4i \)
- Modulus: \( r = \sqrt{4^2 + 4^2} = \sqrt{32} = 4\sqrt{2} \)
- Argument: \( \theta = \tan^{-1}(1) = \frac{\pi}{4} \)
- Euler form: \( z = 4\sqrt{2} \cdot e^{i\frac{\pi}{4}} \)
2. \( z = 2e^{i\frac{\pi}{4}} \Rightarrow z^3 = ? \)
- Use: \( z^n = r^n e^{in\theta} \)
- \( z^3 = 2^3 e^{i3\cdot \frac{\pi}{4}} = 8e^{i\frac{3\pi}{4}} \)
Example
Given: \( z = 3 + 3\sqrt{3}i \)
Convert to: Modulus–Argument (Polar) Form & Euler Form.
▶️ Answer/Explanation
\( r = |z| = \sqrt{3^2 + (3\sqrt{3})^2} = \sqrt{9 + 27} = \sqrt{36} = 6 \)
\( \theta = \tan^{-1}\left(\frac{3\sqrt{3}}{3}\right) = \tan^{-1}(\sqrt{3}) = \frac{\pi}{3} \)
Polar form
\( z = 6(\cos \frac{\pi}{3} + i \sin \frac{\pi}{3}) \)
Euler form
\( z = 6e^{i\frac{\pi}{3}} \)
Complex Number Operation
Complex Number Operation
Sum (Addition/Subtraction) in Cartesian Form
If \( z_1 = a + bi \) and \( z_2 = c + di \), then:
\( z_1 \pm z_2 = (a \pm c) + (b \pm d)i \)
Geometric Interpretation: Addition of complex numbers is like vector addition in the complex plane – the result is the diagonal of the parallelogram formed.
Product in Polar or Euler Form
Let \( z_1 = r_1 \text{cis} \theta_1 \), \( z_2 = r_2 \text{cis} \theta_2 \), or \( z_1 = r_1 e^{i\theta_1} \), \( z_2 = r_2 e^{i\theta_2} \), then:
\( z_1 z_2 = r_1 r_2 \text{cis}(\theta_1 + \theta_2) \) or \( z_1 z_2 = r_1 r_2 e^{i(\theta_1 + \theta_2)} \)
Geometric Interpretation: Multiplication scales the length and rotates the point by the sum of angles.
Quotient in Polar or Euler Form
Let \( z_1 = r_1 \text{cis} \theta_1 \), \( z_2 = r_2 \text{cis} \theta_2 \), or \( z_1 = r_1 e^{i\theta_1} \), \( z_2 = r_2 e^{i\theta_2} \), then:
\( \frac{z_1}{z_2} = \frac{r_1}{r_2} \text{cis}(\theta_1 – \theta_2) \) or \( \frac{z_1}{z_2} = \frac{r_1}{r_2} e^{i(\theta_1 – \theta_2)} \)
Geometric Interpretation: Division scales the modulus and rotates in the opposite direction of the divisor’s argument.
Example : Sum in Cartesian Form
Given: \( z_1 = 4 + 3i \), \( z_2 = -2 + 5i \)
Find: \( z_1 + z_2 \)
▶️ Answer/Explanation
Real part: \( 4 + (-2) = 2 \)
Imaginary part: \( 3i + 5i = 8i \)
Answer: \( z_1 + z_2 = 2 + 8i \)
Example : Product in Polar Form
Given: \( z_1 = 3\text{cis}45^\circ \), \( z_2 = 2\text{cis}30^\circ \)
Find: \( z_1 \cdot z_2 \)
▶️ Answer/Explanation
Multiply moduli: \( 3 \cdot 2 = 6 \)
Add arguments: \( 45^\circ + 30^\circ = 75^\circ \)
Answer: \( z_1 \cdot z_2 = 6\text{cis}75^\circ \)
Example : Quotient in Euler Form
Given: \( z_1 = 8e^{i\frac{\pi}{3}} \), \( z_2 = 2e^{i\frac{\pi}{6}} \)
Find: \( \frac{z_1}{z_2} \)
▶️ Answer/Explanation
Divide moduli: \( \frac{8}{2} = 4 \)
Subtract exponents: \( \frac{\pi}{3} – \frac{\pi}{6} = \frac{\pi}{6} \)
Answer: \( \frac{z_1}{z_2} = 4e^{i\frac{\pi}{6}} \)
