IB Mathematics AA Intersections of a line with a planes Study Notes - New Syllabus
IB Mathematics AA Intersections of a line with a planes Study Notes
IB Mathematics AA Intersections of a line with a planes Notes Offer a clear explanation of Intersections of a line with a planes, including various formula, rules, exam style questions as example to explain the topics. Worked Out examples and common problem types provided here will be sufficient to cover for topic Intersections of a line with a planes.
Intersections of Lines and Planes
Intersection of a line with a plane:
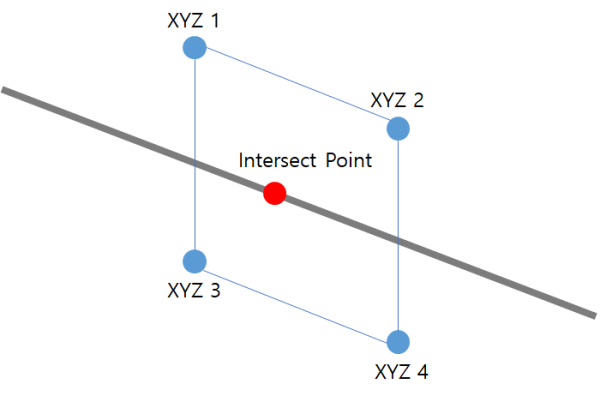
Given line: \( \mathbf{r} = \mathbf{a} + t \mathbf{b} \)
Given plane: \( \mathbf{r} \cdot \mathbf{n} = d \) or \( Ax + By + Cz = D \)
Substitute parametric equation of the line into the plane and solve for \( t \).
Intersection of two planes:
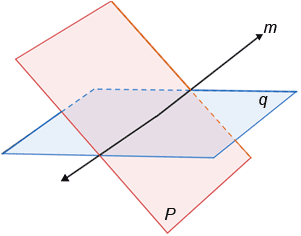
If planes are not parallel, their intersection is a line.
Direction vector of the line: \( \mathbf{d} = \mathbf{n_1} \times \mathbf{n_2} \)
Find a point on both planes and write: \( \mathbf{r} = \mathbf{p} + s \mathbf{d} \)
Intersection of three planes:

Solve the system of equations:
Unique solution: All planes meet at a point.
Infinite solutions: Planes intersect along a common line.
No solution: Planes do not all meet (inconsistent system).
Example :
Find the point where the line \( \mathbf{r} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + t \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix} \) meets the plane \( 3x – y + 2z = 10 \).
▶️Answer/Explanation
Substitute into plane:
\( 3(1 + 2t) – (2 – t) + 2(3 + t) = 10 \)
\( 3 + 6t – 2 + t + 6 + 2t = 10 \Rightarrow 7 + 9t = 10 \Rightarrow t = \frac{1}{9} \)
Point:
\( \mathbf{r} = \begin{pmatrix} 1 + 2 \cdot \frac{1}{9} \\ 2 – \frac{1}{9} \\ 3 + \frac{1}{9} \end{pmatrix} = \begin{pmatrix} \frac{11}{9} \\ \frac{17}{9} \\ \frac{28}{9} \end{pmatrix} \)
Example :
Find the line of intersection of:
- \( x + y + z = 6 \)
- \( 2x – y + z = 3 \)
▶️ Answer/Explanation
Subtract equations:
\( x – 2y = -3 \Rightarrow x = -3 + 2y \)
Let \( y = t \). Then:
\( z = 6 – x – y = 6 – (-3 + 2t) – t = 9 – 3t \)
Line of intersection:
\( \mathbf{r} = \begin{pmatrix} -3 \\ 0 \\ 9 \end{pmatrix} + t \begin{pmatrix} 2 \\ 1 \\ -3 \end{pmatrix} \)
Example :
- \( x + y + z = 6 \)
- \( 2x – y + z = 3 \)
- \( 3x + y – z = 2 \)
▶️Answer/Explanation
Solving system yields:
Unique solution: \( x = 1 \), \( y = 2 \), \( z = 3 \)
Angles between Lines and Planes
Angle between a line and a plane:
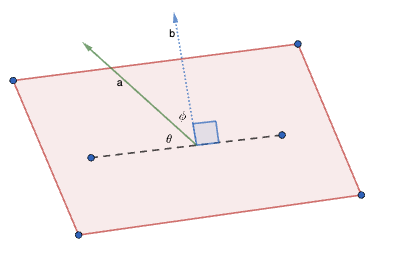
The angle \( \theta \) between a line (with direction vector \( \mathbf{d} \)) and a plane (with normal \( \mathbf{n} \)) satisfies:
\( \sin \theta = \frac{|\mathbf{d} \cdot \mathbf{n}|}{|\mathbf{d}| \, |\mathbf{n}|} \)
Angle between two planes:
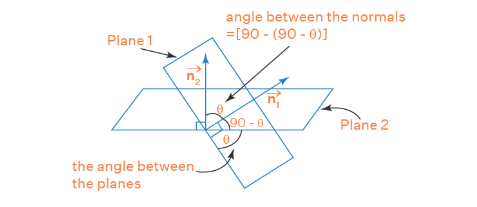
The angle \( \phi \) between two planes is the angle between their normals:
\( \cos \phi = \frac{|\mathbf{n_1} \cdot \mathbf{n_2}|}{|\mathbf{n_1}| \, |\mathbf{n_2}|} \)
Example :
Find the angle between the line \( \mathbf{r} = \begin{pmatrix} 1 \\ 0 \\ 2 \end{pmatrix} + t \begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix} \) and the plane \( x + 2y + 2z = 5 \).
▶️ Answer/Explanation
Direction vector: \( \mathbf{d} = \begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix} \), normal: \( \mathbf{n} = \begin{pmatrix} 1 \\ 2 \\ 2 \end{pmatrix} \)
\( \sin \theta = \frac{|\mathbf{d} \cdot \mathbf{n}|}{|\mathbf{d}| \, |\mathbf{n}|} = \frac{|2 \cdot 1 + 1 \cdot 2 + 2 \cdot 2|}{\sqrt{2^2 + 1^2 + 2^2} \sqrt{1^2 + 2^2 + 2^2}} \)
\( = \frac{|2 + 2 + 4|}{\sqrt{9} \sqrt{9}} = \frac{8}{3 \cdot 3} = \frac{8}{9} \)
\( \theta = \arcsin \left( \frac{8}{9} \right) \approx 62.7^\circ \)
Example :
Find the angle between the planes:
- \( 2x – y + z = 4 \)
- \( x + 2y – z = 1 \)
▶️ Answer/Explanation
Normals: \( \mathbf{n_1} = \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix} \), \( \mathbf{n_2} = \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix} \)
\( \cos \phi = \frac{|\mathbf{n_1} \cdot \mathbf{n_2}|}{|\mathbf{n_1}| |\mathbf{n_2}|} \)
\( = \frac{|2 \cdot 1 + (-1) \cdot 2 + 1 \cdot (-1)|}{\sqrt{4 + 1 + 1} \sqrt{1 + 4 + 1}} \)
\( = \frac{|2 – 2 – 1|}{\sqrt{6} \sqrt{6}} = \frac{1}{6} \)
\( \phi = \arccos \left( \frac{1}{6} \right) \approx 80.4^\circ \)
