IB Mathematics AA Pythagorean identities Study Notes
IB Mathematics AA Pythagorean identities Study Notes
IB Mathematics AA Pythagorean identities Study Notes Offer a clear explanation of Pythagorean identities , including various formula, rules, exam style questions as example to explain the topics. Worked Out examples and common problem types provided here will be sufficient to cover for topic Pythagorean identities.
Pythagorean Identity
Pythagorean Identity
The identity is: \( \cos^2 \theta + \sin^2 \theta = 1 \)
This identity holds true for any real value of \( \theta \).
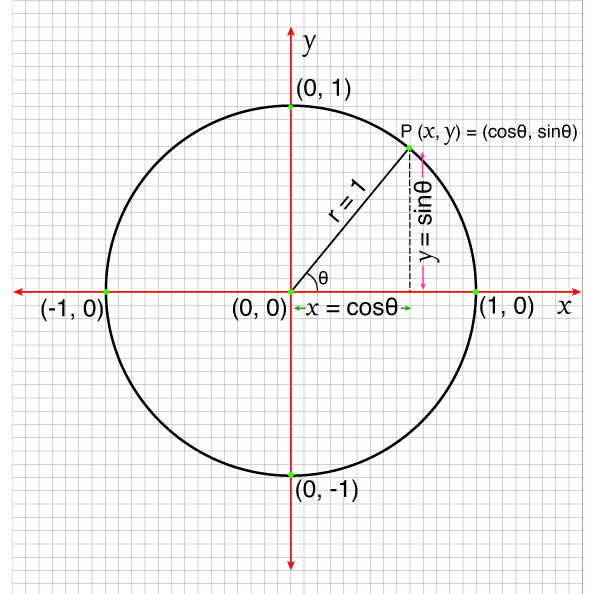
It is derived from the unit circle where any point on the circle satisfies: \( x^2 + y^2 = 1^2 \) and where \( x = \cos \theta \), \( y = \sin \theta \).
Example
Verify the identity for \( \theta = 45^\circ \).
▶️Answer/Explanation
We know: \[ \sin 45^\circ = \cos 45^\circ = \frac{\sqrt{2}}{2} \]
Substitute into the identity: \[ \left( \frac{\sqrt{2}}{2} \right)^2 + \left( \frac{\sqrt{2}}{2} \right)^2 = \frac{2}{4} + \frac{2}{4} = 1 \]
The identity holds for \( \theta = 45^\circ \).
Double Angle Identities
Double Angle Identities
Sine Double Angle Identity: $ \sin(2\theta) = 2 \sin \theta \cos \theta $
Cosine Double Angle Identity: $ \cos(2\theta) = \cos^2 \theta – \sin^2 \theta $ or equivalently: $ \cos(2\theta) = 2 \cos^2 \theta – 1 \quad \text{or} \quad \cos(2\theta) = 1 – 2 \sin^2 \theta $
These identities are useful for simplifying expressions, solving equations, and in integration.
Example
Given \( \theta = 30^\circ \), find \( \sin(60^\circ) \) and \( \cos(60^\circ) \) using double angle identities.
▶️Answer/Explanation
$ \sin 30^\circ = 0.5, \quad \cos 30^\circ = \frac{\sqrt{3}}{2} $
Use sine double angle identity:
$ \sin 60^\circ = \sin(2 \times 30^\circ) = 2 \sin 30^\circ \cos 30^\circ $
$ = 2 \times 0.5 \times \frac{\sqrt{3}}{2} = \frac{\sqrt{3}}{2} $
Use cosine double angle identity:
$ \cos 60^\circ = \cos(2 \times 30^\circ) = \cos^2 30^\circ – \sin^2 30^\circ $
$ = \left( \frac{\sqrt{3}}{2} \right)^2 – (0.5)^2 = \frac{3}{4} – \frac{1}{4} = 0.5 $
Relationships Between Trigonometric Ratios
Relationships Between Trigonometric Ratios
The trigonometric functions are related through identities:
\( \tan \theta = \frac{\sin \theta}{\cos \theta} \)
\( \sin^2 \theta + \cos^2 \theta = 1 \)
\( \sin 2x = 2 \sin x \cos x \)
These relationships allow us to find other ratios without determining \( \theta \) or \( x \) explicitly.
Example
Given \( \sin \theta = \frac{3}{5} \), find the possible values of \( \tan \theta \) (without finding \( \theta \)).
▶️Answer/Explanation
From \( \sin^2 \theta + \cos^2 \theta = 1 \): \[ \left( \frac{3}{5} \right)^2 + \cos^2 \theta = 1 \]
\[ \frac{9}{25} + \cos^2 \theta = 1 \] \[ \cos^2 \theta = 1 – \frac{9}{25} = \frac{16}{25} \]
So \( \cos \theta = \pm \frac{4}{5} \).
Then, \[ \tan \theta = \frac{\sin \theta}{\cos \theta} = \frac{3/5}{\pm 4/5} = \pm \frac{3}{4} \]
Example
Given \( \cos x = \frac{3}{4} \) and \( x \) is acute, find \( \sin 2x \) (without finding \( x \)).
▶️Answer/Explanation
Since \( x \) is acute, \( \sin x \) is positive. \[ \sin^2 x = 1 – \cos^2 x = 1 – \left( \frac{3}{4} \right)^2 = 1 – \frac{9}{16} = \frac{7}{16} \] \[ \sin x = \frac{\sqrt{7}}{4} \]
Use \( \sin 2x = 2 \sin x \cos x \): \[ \sin 2x = 2 \times \frac{\sqrt{7}}{4} \times \frac{3}{4} = \frac{3 \sqrt{7}}{8} \]
