IB Mathematics AA Scalar product of two vectors Study Notes
IB Mathematics AA Scalar product of two vectors Study Notes
IB Mathematics AA Scalar product of two vectors Notes Offer a clear explanation of Scalar product of two vectors, including various formula, rules, exam style questions as example to explain the topics. Worked Out examples and common problem types provided here will be sufficient to cover for topic Scalar product of two vectors.
Scalar (Dot) Product of Two Vectors
Scalar (Dot) Product of Two Vectors
The scalar product (or dot product) of two vectors \( \mathbf{a} \) and \( \mathbf{b} \) is given by:
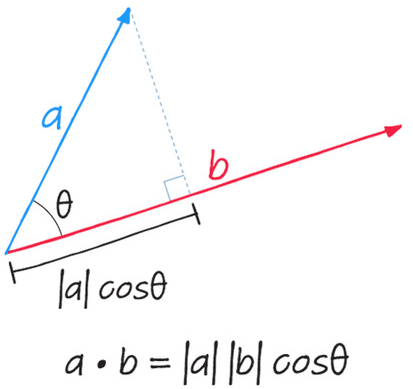
\( \mathbf{a} \cdot \mathbf{b} = |\mathbf{a}| |\mathbf{b}| \cos \theta \)
where:
- \( |\mathbf{a}| \) and \( |\mathbf{b}| \) are the magnitudes of the vectors
- \( \theta \) is the angle between \( \mathbf{a} \) and \( \mathbf{b} \)
Alternative form (component-wise):
If \( \mathbf{a} = (a_1, a_2) \) and \( \mathbf{b} = (b_1, b_2) \), then
In 2D, \( \mathbf{a} \cdot \mathbf{b} = a_1 b_1 + a_2 b_2 \)
In 3D, \( \mathbf{a} \cdot \mathbf{b} = a_1 b_1 + a_2 b_2 + a_3 b_3 \)
Properties of the Scalar (Dot) Product:
- Commutative: \( \mathbf{v} \cdot \mathbf{w} = \mathbf{w} \cdot \mathbf{v} \)
- Distributive: \( \mathbf{u} \cdot (\mathbf{v} + \mathbf{w}) = \mathbf{u} \cdot \mathbf{v} + \mathbf{u} \cdot \mathbf{w} \)
- Scalar multiplication: \( (k \mathbf{v}) \cdot \mathbf{w} = k (\mathbf{v} \cdot \mathbf{w}) \)
- Magnitude squared: \( \mathbf{v} \cdot \mathbf{v} = |\mathbf{v}|^2 \)
Example:
Let \( \mathbf{u} = (1,2) \), \( \mathbf{v} = (3,4) \), \( \mathbf{w} = (5,6) \), and \( k = 2 \). Verify the properties:
- Commutative
- Distributive
- multiplication
- Magnitude squared
▶️ Answer/Explanation
Commutative:
\( \mathbf{v} \cdot \mathbf{w} = 3 \times 5 + 4 \times 6 = 15 + 24 = 39 \)
\( \mathbf{w} \cdot \mathbf{v} = 5 \times 3 + 6 \times 4 = 15 + 24 = 39 \)
Distributive:
\( \mathbf{v} + \mathbf{w} = (8,10) \)
\( \mathbf{u} \cdot ( \mathbf{v} + \mathbf{w} ) = 1 \times 8 + 2 \times 10 = 8 + 20 = 28 \)
\( \mathbf{u} \cdot \mathbf{v} + \mathbf{u} \cdot \mathbf{w} = (1 \times 3 + 2 \times 4) + (1 \times 5 + 2 \times 6) = (3 + 8) + (5 + 12) = 11 + 17 = 28 \)
Scalar multiplication:
\( (2 \mathbf{v}) \cdot \mathbf{w} = (6,8) \cdot (5,6) = 6 \times 5 + 8 \times 6 = 30 + 48 = 78 \)
\( 2 (\mathbf{v} \cdot \mathbf{w}) = 2 \times 39 = 78 \)
Magnitude squared:
\( \mathbf{v} \cdot \mathbf{v} = 3^2 + 4^2 = 9 + 16 = 25 = |\mathbf{v}|^2 \)
Angle Between Two Vectors
Angle Between Two Vectors
The angle \( \theta \) between two vectors \( \mathbf{a} \) and \( \mathbf{b} \) is given by:
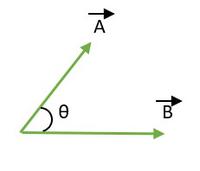
\( \cos \theta = \frac{ \mathbf{a} \cdot \mathbf{b} }{ |\mathbf{a}| \, |\mathbf{b}| } \)
where:
- \( \mathbf{a} \cdot \mathbf{b} \) is the scalar (dot) product of the vectors
- \( |\mathbf{a}| \) and \( |\mathbf{b}| \) are the magnitudes of the vectors
- \( 0^\circ \leq \theta \leq 180^\circ \)
Example:
\( \mathbf{a} = (2, -1, 2) \) and \( \mathbf{b} = (1, 2, 3) \)
▶️ Answer/Explanation
\( \mathbf{a} \cdot \mathbf{b} = 2 \times 1 + (-1) \times 2 + 2 \times 3 = 2 – 2 + 6 = 6 \)
\( |\mathbf{a}| = \sqrt{2^2 + (-1)^2 + 2^2} = \sqrt{4 + 1 + 4} = \sqrt{9} = 3 \)
\( |\mathbf{b}| = \sqrt{1^2 + 2^2 + 3^2} = \sqrt{1 + 4 + 9} = \sqrt{14} \)
\( \cos \theta = \frac{6}{3 \sqrt{14}} = \frac{2}{\sqrt{14}} \)
\( \theta = \arccos \left( \frac{2}{\sqrt{14}} \right) \approx 56.3^\circ \)
Perpendicular & Parallel Vectors:
Perpendicular (Orthogonal) Vectors:
Two vectors \( \mathbf{a} \) and \( \mathbf{b} \) are perpendicular if:
\( \mathbf{a} \cdot \mathbf{b} = 0 \)
Parallel Vectors:
Two vectors \( \mathbf{a} \) and \( \mathbf{b} \) are parallel if:
\( \mathbf{a} = k \mathbf{b} \quad \text{for some scalar } k \)
In other words, one vector is a scalar multiple of the other.

Example:
Check if the given pairs of vectors are perpendicular or parallel
\( \mathbf{a} = (2, 3) \), \( \mathbf{b} = (-3, 2) \)
\( \mathbf{p} = (4, 6) \), \( \mathbf{q} = (2, 3) \)
▶️ Answer/Explanation
Check perpendicularity:
\( \mathbf{a} \cdot \mathbf{b} = 2 \times (-3) + 3 \times 2 = -6 + 6 = 0 \)
Vectors \( \mathbf{a} \) and \( \mathbf{b} \) are perpendicular.
Check parallelism:
\( \mathbf{p} = 2 \times \mathbf{q} \) since \( (4, 6) = 2 \times (2, 3) \)
Vectors \( \mathbf{p} \) and \( \mathbf{q} \) are parallel.
