IB Mathematics AA Vector product of two vectors Study Notes
IB Mathematics AA vector product of two vectors Study Notes
IB Mathematics AA Vector product of two vectors Notes Offer a clear explanation of Vector product of two vectors, including various formula, rules, exam style questions as example to explain the topics. Worked Out examples and common problem types provided here will be sufficient to cover for topic Vector product of two vectors.
Vector Product (Cross Product) of Two Vectors
Vector Product (Cross Product) of Two Vectors
The vector product or cross product of two vectors a and b is a vector that is perpendicular to both a and b. It is denoted by a × b.
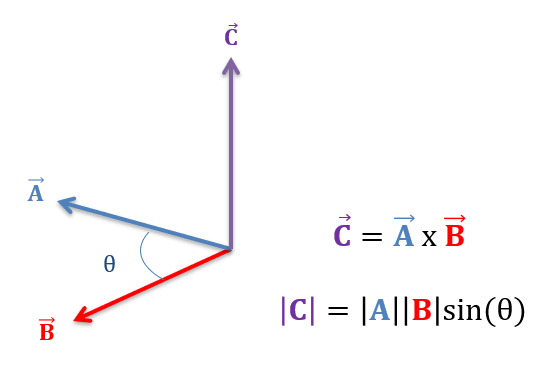
\( \mathbf{a} \times \mathbf{b} = |\mathbf{a}| |\mathbf{b}| \sin \theta \, \mathbf{n} \)
- \( |\mathbf{a}|, |\mathbf{b}| \) are the magnitudes of the vectors.
- \( \theta \) is the angle between a and b, \( 0 \le \theta \le \pi \).
- \( \mathbf{n} \) is a unit vector perpendicular to both a and b (right-hand rule).
Formula for components:
If \( \mathbf{a} = \begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix} \), \( \mathbf{b} = \begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix} \), then
\( \mathbf{a} \times \mathbf{b} = \begin{pmatrix} a_2 b_3 – a_3 b_2 \\ a_3 b_1 – a_1 b_3 \\ a_1 b_2 – a_2 b_1 \end{pmatrix} \)
Geometrical interpretation:
- The vector product gives a vector normal (perpendicular) to the plane containing a and b.
- The magnitude of \( \mathbf{a} \times \mathbf{b} \) equals the area of the parallelogram formed by a and b.
Example
Find the vector product of \( \mathbf{a} = \begin{pmatrix} 2 \\ -1 \\ 3 \end{pmatrix} \) and \( \mathbf{b} = \begin{pmatrix} 0 \\ 4 \\ -2 \end{pmatrix} \).
▶️ Answer/Explanation
\( \mathbf{a} \times \mathbf{b} = \begin{pmatrix} (-1)(-2) – (3)(4) \\ (3)(0) – (2)(-2) \\ (2)(4) – (-1)(0) \end{pmatrix} \)
\( = \begin{pmatrix} 2 – 12 \\ 0 + 4 \\ 8 – 0 \end{pmatrix} \) = \( \begin{pmatrix} -10 \\ 4 \\ 8 \end{pmatrix} \)
Answer: The cross product is \( \mathbf{a} \times \mathbf{b} = \begin{pmatrix} -10 \\ 4 \\ 8 \end{pmatrix} \).
The magnitude is:
\( |\mathbf{a} \times \mathbf{b}| = \sqrt{(-10)^2 + 4^2 + 8^2} \) = \( \sqrt{100 + 16 + 64} = \sqrt{180} \approx 13.42 \)
This represents the area of the parallelogram formed by \( \mathbf{a} \) and \( \mathbf{b} \).
Properties of the Vector Product (Cross Product)
Properties of the Vector Product (Cross Product)
Perpendicularity: The cross product \( \mathbf{a} \times \mathbf{b} \) is perpendicular to both \( \mathbf{a} \) and \( \mathbf{b} \).
\( |\mathbf{a} \times \mathbf{b}| = |\mathbf{a}| |\mathbf{b}| \sin \theta \)
where \( \theta \) is the angle between \( \mathbf{a} \) and \( \mathbf{b} \), \( 0 \le \theta \le \pi \).
Anti-commutative property:
\( \mathbf{a} \times \mathbf{b} = -(\mathbf{b} \times \mathbf{a}) \)
Distributive over addition:
\( \mathbf{a} \times (\mathbf{b} + \mathbf{c}) = \mathbf{a} \times \mathbf{b} + \mathbf{a} \times \mathbf{c} \)
Zero vector:
\( \mathbf{a} \times \mathbf{a} = \mathbf{0} \)
The cross product of a vector with itself is the zero vector.
Scalar multiplication:
\( (k \mathbf{a}) \times \mathbf{b} = k (\mathbf{a} \times \mathbf{b}) \)
\( \mathbf{a} \times (k \mathbf{b}) = k (\mathbf{a} \times \mathbf{b}) \)
where \( k \) is a scalar.
Parallel vectors:
If \( \mathbf{a} \) and \( \mathbf{b} \) are parallel, then \( \mathbf{a} \times \mathbf{b} = \mathbf{0} \).
Right-hand rule:
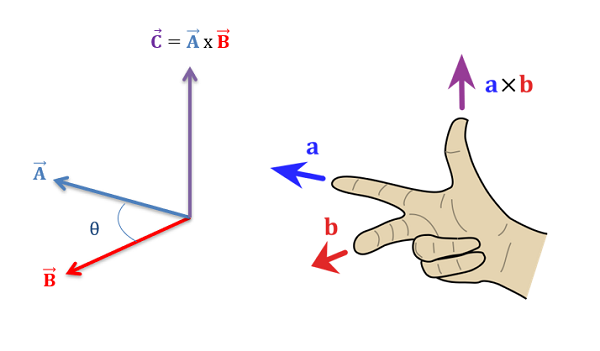
The direction of \( \mathbf{a} \times \mathbf{b} \) is given by the right-hand rule.
Example
A rectangular billboard lies in a plane defined by two vectors: \( \mathbf{a} = \begin{pmatrix} 5 \\ 0 \\ 0 \end{pmatrix} \) (length direction) and \( \mathbf{b} = \begin{pmatrix} 0 \\ 3 \\ 0 \end{pmatrix} \) (height direction).
Find a vector that is perpendicular to the surface of the billboard.
▶️ Answer/Explanation
cross product:
\( \mathbf{a} \times \mathbf{b} = \begin{pmatrix} (0)(0) – (0)(3) \\ (0)(0) – (5)(0) \\ (5)(3) – (0)(0) \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 15 \end{pmatrix} \)
The vector \( \mathbf{n} = \begin{pmatrix} 0 \\ 0 \\ 15 \end{pmatrix} \) is perpendicular to both sides of the billboard. This means it points directly outward, perpendicular to the plane.
normalize this:
\( \mathbf{\hat{n}} = \frac{\mathbf{n}}{|\mathbf{n}|} = \frac{1}{15} \begin{pmatrix} 0 \\ 0 \\ 15 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \)
This is the unit normal vector.
Geometric Interpretation of \( | \mathbf{a} \times \mathbf{b} | \)
Geometric Interpretation of \( | \mathbf{a} \times \mathbf{b} | \)
The magnitude of the cross product \( | \mathbf{a} \times \mathbf{b} | \) represents the area of the parallelogram formed by the vectors \( \mathbf{a} \) and \( \mathbf{b} \).
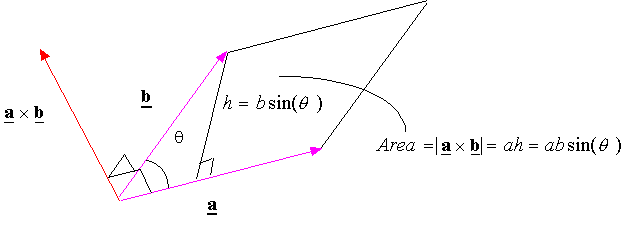
\( | \mathbf{a} \times \mathbf{b} | = | \mathbf{a} | \, | \mathbf{b} | \sin \theta \)
where \( \theta \) is the angle between \( \mathbf{a} \) and \( \mathbf{b} \).
The cross product vector is perpendicular to the plane containing \( \mathbf{a} \) and \( \mathbf{b} \).
Example
Find the area of the parallelogram formed by the vectors \( \mathbf{a} = \begin{pmatrix} 3 \\ 0 \\ 0 \end{pmatrix} \) and \( \mathbf{b} = \begin{pmatrix} 0 \\ 4 \\ 0 \end{pmatrix} \).
▶️ View Solution
cross product:
\( \mathbf{a} \times \mathbf{b} = \begin{pmatrix} 0 \\ 0 \\ (3)(4)-(0)(0) \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 12 \end{pmatrix} \)
Magnitude of cross product:
\( | \mathbf{a} \times \mathbf{b} | = 12 \)
The area of the parallelogram is 12 square units.
