IB Mathematics AI AHL Modulus–argument (polar) form Study Notes - New Syllabus

IB Mathematics AI AHL Modulus–argument (polar) form Study Notes

LEARNING OBJECTIVE

Modulus–argument (polar) form

Key Concepts:

Modulus–argument (polar) form:
Exponential form
Conversion
Geometric interpretation of complex numbers

A complex number $ z = x + yi $ can also be described using polar coordinates $(r, \theta)$:

$ r = $ length of the vector (modulus $ |z| $).
$ \theta = $ angle between the $ x $-axis and the vector (argument $ \arg(z) $).

♦Relations:

$ \cos \theta = \frac{x}{r}, \quad \sin \theta = \frac{y}{r}, \quad \tan \theta = \frac{y}{x} $

Thus, $ z $ can be written in polar form:

$ z = r (\cos \theta + i \sin \theta) $

♦REMARK:

The argument $ \theta $ is not unique. For the principal argument, we agree:

$ -180^\circ < \theta \leq 180^\circ \quad \text{or} \quad -\pi < \theta \leq \pi $

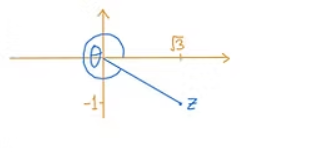
Example

Convert $z = \sqrt{3} – i$ to polar form.

Sketch the final answer on Argand plane.

▶️Answer/Explanation

Solution:

$r = \sqrt{(\sqrt{3})^2 + (-1)^2} = \sqrt{4} = 2$
$\tan \theta = \frac{-1}{\sqrt{3}}$, so $\theta = 150^\circ$ or $330^\circ$?

Since $z$ is in the fourth quadrant:

$\therefore z = 2(\cos 330^\circ + i \sin 330^\circ) = 2 \operatorname{cis} 330^\circ$

Argand diagram

Example

Find the polar form of:

$ z_1 = 1 + i : ? $
$ z_2 = -1 – i : ? $
$ z_3 = 1 – i : ? $
$ z_4 = -1 + i : ? $

▶️Answer/Explanation

Solution:

$ z_1 = 1 + i $: $ \theta = \frac{\pi}{4} $
$ z_2 = -1 – i $: $ \theta = \frac{5\pi}{4} $
$ z_3 = 1 – i $: $ \theta = -\frac{\pi}{4} $
$ z_4 = -1 + i $: $ \theta = \frac{3\pi}{4} $

All have modulus $ \sqrt{2} $.

♦Transformation from Cartesian to Polar Form:

Given $ z = x + yi $, find $ r $ and $ \theta $:
$ r = |z| = \sqrt{x^2 + y^2} $
$ \tan \theta = \frac{y}{x}, \quad \text{considering the quadrant of } (x, y). $

♦Transformation from Polar to Cartesian Form:

Simply compute $ x = r \cos \theta $ and $ y = r \sin \theta $.

GDC Tip: Use the “COMPLEX” mode to switch between forms.

♦CIS FORM AND EULER’S FORM

CIS Form: $ z = r \operatorname{cis} \theta = r (\cos \theta + i \sin \theta) $.
Euler’s Form: $ z = r e^{i\theta} $, where $ e^{i\theta} = \cos \theta + i \sin \theta $.

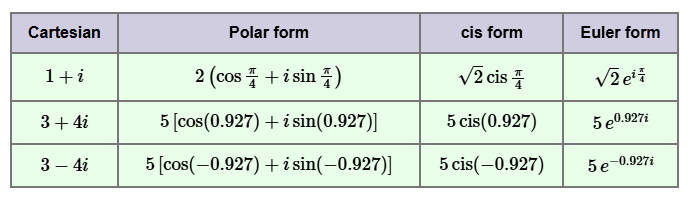
Example

Find All forms of

$ z_1 = 1 + i $,

$ z_2 = 3 + 4i $,

$ z_3 = 3 – 4i $:

▶️Answer/Explanation

Solution:

♦NOTICE

Any complex number with modulus 1 has polar form $ z = \operatorname{cis} \theta $.

For real numbers $ \pm a $, the argument is $ 0 $ (if $ a > 0 $) or $ \pi $ (if $ a < 0 $).
For imaginary numbers $ \pm ai $, the argument is $ \frac{\pi}{2} $ or $ -\frac{\pi}{2} $.
The conjugate of $ z = r (\cos \theta + i \sin \theta) $ is $ \overline{z} = r (\cos \theta – i \sin \theta) = r \operatorname{cis}(-\theta) $.

For $ z_1 = r_1 \operatorname{cis} \theta_1 $ and $ z_2 = r_2 \operatorname{cis} \theta_2 $:

Product:

$ z_1 z_2 = r_1 r_2 \operatorname{cis}(\theta_1 + \theta_2) $.

Quotient:

$ \frac{z_1}{z_2} = \frac{r_1}{r_2} \operatorname{cis}(\theta_1 – \theta_2) $.

Power (De Moivre’s Law):

$ z^n = r^n \operatorname{cis}(n \theta) $.

♦Properties:

Modulus:

$ |z_1 z_2| = |z_1| |z_2| $, $ \left| \frac{z_1}{z_2} \right| = \frac{|z_1|}{|z_2|} $, $ |z^n| = |z|^n $.

Argument:

$ \arg(z_1 z_2) = \arg(z_1) + \arg(z_2) $, $ \arg\left( \frac{z_1}{z_2} \right) = \arg(z_1) – \arg(z_2) $, $ \arg(z^n) = n \arg(z) $.

Example

$ z = 2 \operatorname{cis} \frac{\pi}{6} $ and $ w = \operatorname{cis} \frac{\pi}{3} $.

(i) $ z w=?$

(ii) $ \frac{z}{w}=?$

(iii) $ z^6=?$

▶️Answer/Explanation

Solution:

$ z w = 2 \operatorname{cis} \frac{\pi}{2} = 2i $.
$ \frac{z}{w} = 2 \operatorname{cis}\left( -\frac{\pi}{6} \right) = \sqrt{3} – i $.
$ z^6 = 64 \operatorname{cis} \pi = -64 $.

Example

Calculate

$ (1 + i)^{10} $

Answer it in form of $i$

▶️Answer/Explanation

Solution:

$ 1 + i = \sqrt{2} \operatorname{cis} \frac{\pi}{4} $.
$ (1 + i)^{10} = (\sqrt{2})^{10} \operatorname{cis} \frac{10\pi}{4} = 32 \operatorname{cis} \frac{\pi}{2} = 32i $.

Example

Using De Moivre’s theorem,

Derive trigonometric identities:

$ z = \operatorname{cis} \theta \Rightarrow z^2 = \cos 2\theta + i \sin 2\theta $.

▶️Answer/Explanation

Solution:

$ z = \operatorname{cis} \theta \Rightarrow z^2 = \cos 2\theta + i \sin 2\theta $.
Also, $ z^2 = (\cos \theta + i \sin \theta)^2 = (\cos^2 \theta – \sin^2 \theta) + i (2 \sin \theta \cos \theta) $.
Comparing gives: $ \cos 2\theta = \cos^2 \theta – \sin^2 \theta $, $ \sin 2\theta = 2 \sin \theta \cos \theta $.

Express sums of sinusoidal functions as a single function:

$ A_1 \cos(x + \theta_1) + A_2 \cos(x + \theta_2) = A \cos(x + \theta) $.

Use Euler’s form:

$ A \cos(x + \theta) = \operatorname{Re}(A e^{i(x + \theta)}) $.

Example

For $ f(x) = 4 \cos x $ and $ g(x) = 3 \cos\left(x + \frac{\pi}{4}\right) $:

Add both Functions.

▶️Answer/Explanation

Solution:

$ f(x) + g(x) = \operatorname{Re}(4 e^{ix} + 3 e^{i(x + \pi/4)}) = \operatorname{Re}(6.48 e^{i(x + 0.334)}) = 6.48 \cos(x + 0.334) $.

Application: Adding waves of the same frequency results in a wave of the same frequency.

Example

For $ V_1(t) = 7 \sin(4t – 1) $ and $ V_2(t) = 2 \sin(4t + 3) $

Add both Functions.

▶️Answer/Explanation

Solution:

$ V_1(t) + V_2(t) = 5.89 \sin(4t – 1.26) $.

Modulus

The modulus represents the distance from the origin to the point in the complex plane.

Argument

The argument represents the angle from the positive real axis to the line connecting the origin to the point.

Multiplication of Complex Numbers

Geometrically, multiplying two complex numbers in polar form:

Multiplies their moduli
Adds their arguments

This results in:

A scaling (change in size based on modulus)
A rotation (change in direction based on angle addition)

Division of Complex Numbers

Geometrically, dividing two complex numbers in polar form:

Divides their moduli
Subtracts their arguments

This results in:

Inverse scaling (shrinking or enlarging)
Rotation in the opposite direction (based on angle subtraction)

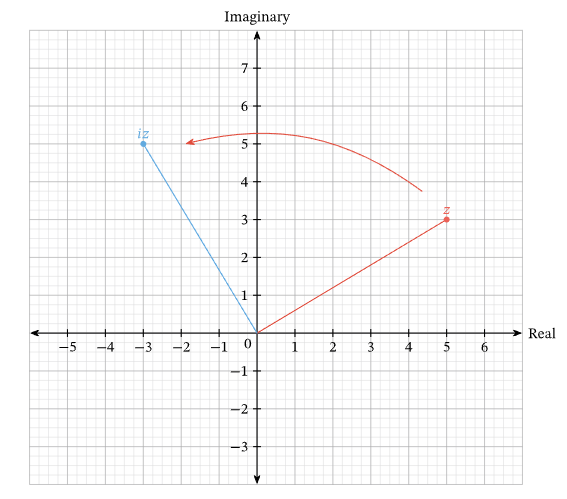
Example

Consider the complex number $z = 5 + 3i$.

If $iz$ is represented on an Argand diagram by the point $A$, in which quadrant of the Argand plane does $A$ lie?

Sketch it on Argand plane.

▶️Answer/Explanation

Solution:

$
\begin{align}
iz &= i(5 + 3i) \\
&= 5i + 3i^2 \\
&= 5i + 3(-1) \\
&= -3 + 5i
\end{align}
$

Now, on an Argand diagram, a complex number $a + bi$ is represented by the point $(a, b)$. So:

$z = 5 + 3i$ corresponds to the point $(5, 3)$
$iz = -3 + 5i$ corresponds to the point $(-3, 5)$

Thus, the point $A$, which represents $iz$, lies in the second quadrant (where real part is negative and imaginary part is positive).

Specifically, the original point was rotated around the origin by an angle of $\frac{\pi}{2}$ radians

Previous Topic Notes

Next Topic Notes

IB Mathematics AI AHL Modulus–argument (polar) form Study Notes - New Syllabus

IB Mathematics AI AHL Modulus–argument (polar) form Study Notes

THE POLAR FORM (MODULUS-ARGUMENT FORM)

CONVERSION BETWEEN DIFFERENT FORMS

PRODUCTS, QUOTIENTS, AND POWERS IN POLAR FORM

ADDING SINUSOIDAL FUNCTIONS

GEOMETRICAL INTERPRETATION OF COMPLEX NUMBERS

Resources

Members

Company