IBDP MAI : Topic 3 Geometry and trigonometry - AHL 3.9 Geometric transformations AI HL Paper 3
Question
Emma, a graphic designer, wants to create an animation in which a sequence of squares is generated by successive enlargements and translations, then rotated about the origin and reduced in size.
Emma outlines her plan with the following storyboards:
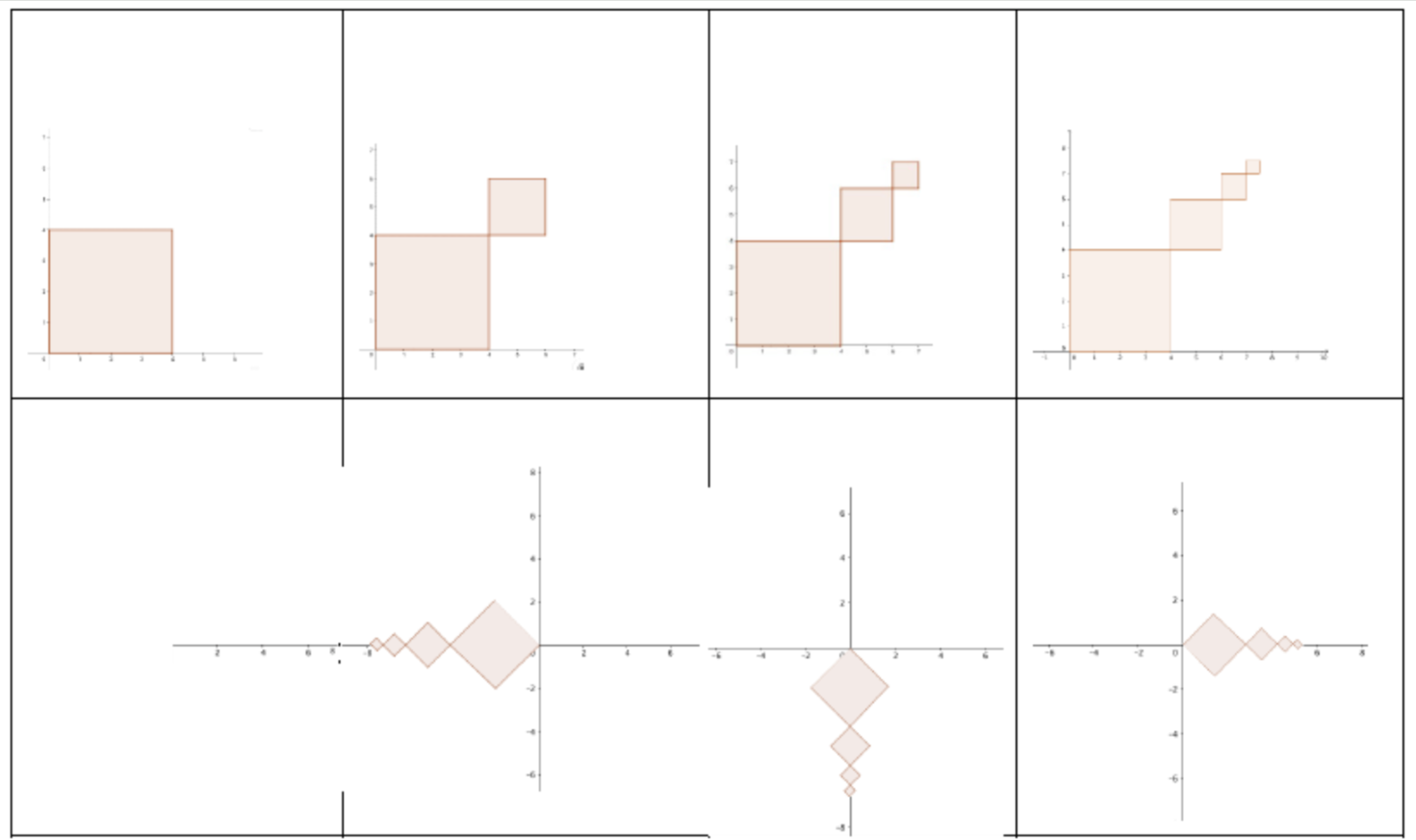
The first four frames of the animation are shown below in greater detail:
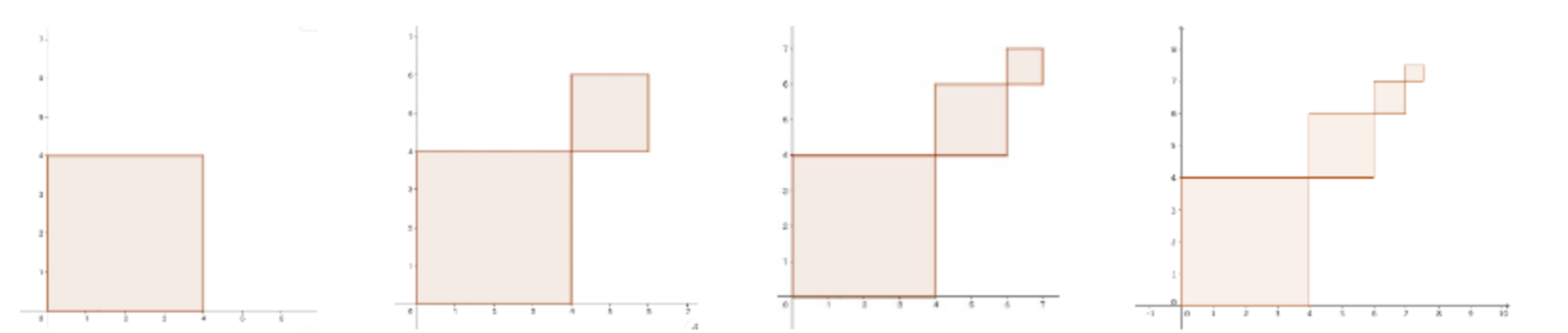
The sides of each successive square are half the size of the adjacent larger square. Let the sequence of squares be \( U_0, U_1, U_2, \ldots \). The first square, \( U_0 \), has sides of length 4 cm.
Emma decides the animation will continue as long as the width of a square is greater than the width of one pixel.
Emma decides to generate the squares using the transformation
\[ \begin{pmatrix} x_n \\ y_n \end{pmatrix} = \boldsymbol{A}_n \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} + \boldsymbol{b}_n \]
where \( \boldsymbol{A}_n \) is a \( 2 \times 2 \) matrix representing an enlargement, \( \boldsymbol{b}_n \) is a \( 2 \times 1 \) column vector representing a translation, \( (x_0, y_0) \) is a point in \( U_0 \), and \( (x_n, y_n) \) is its image in \( U_n \).
By considering the case where \( (x_0, y_0) = (0, 0) \):
Once the sequence of squares is produced, Emma wants to continue the animation by rotating the image counterclockwise about the origin and reducing it in size during the rotation.
Let \( E_\theta \) be the enlargement matrix used when the sequence of squares has been rotated through \( \theta \) degrees. Emma decides the enlargement scale factor, \( s \), should be a linear function of the angle \( \theta \), and after a rotation of 360°, the sequence of squares should be half its original length.
(a) Find an expression for the width of \( U_n \) in centimetres. [2]
(b) Given the width of a pixel is approximately 0.025 cm, find the number of squares in the final image. [3]
(c)
(i) Write down \( \boldsymbol{A}_1 \). [1]
(ii) Write down \( \boldsymbol{A}_n \), in terms of \( n \). [1]
(i) Write down \( \boldsymbol{A}_1 \). [1]
(ii) Write down \( \boldsymbol{A}_n \), in terms of \( n \). [1]
(d)
(i) State the coordinates, \( (x_1, y_1) \), of the image of \( (0, 0) \) in \( U_1 \). [1]
(ii) Hence find \( \boldsymbol{b}_1 \). [2]
(iii) Show that \( \boldsymbol{b}_n = \begin{pmatrix} 8 \left( 1 – 2^{-n} \right) \\ 8 \left( 1 – 2^{-n} \right) \end{pmatrix} \). [3]
(i) State the coordinates, \( (x_1, y_1) \), of the image of \( (0, 0) \) in \( U_1 \). [1]
(ii) Hence find \( \boldsymbol{b}_1 \). [2]
(iii) Show that \( \boldsymbol{b}_n = \begin{pmatrix} 8 \left( 1 – 2^{-n} \right) \\ 8 \left( 1 – 2^{-n} \right) \end{pmatrix} \). [3]
(e) Hence or otherwise, find the coordinates of the top left-hand corner of \( U_7 \). [3]
(f)
(i) Find \( s \), in the form \( s(\theta) = m \theta + c \). [4]
(ii) Write down \( E_\theta \). [1]
(iii) Hence find the image of \( (1, 1) \) after it is rotated 135° and enlarged. [4]
(i) Find \( s \), in the form \( s(\theta) = m \theta + c \). [4]
(ii) Write down \( E_\theta \). [1]
(iii) Hence find the image of \( (1, 1) \) after it is rotated 135° and enlarged. [4]
(g) Find the value of \( \theta \) at which the enlargement scale factor equals zero. [1]
(h) After the enlargement scale factor equals zero, Emma continues to rotate the image for another two revolutions. Describe the animation for these two revolutions, stating the final position of the sequence of squares. [2]
▶️ Answer/Explanation
Markscheme
(a)
The side length of \( U_0 \) is 4 cm, and each successive square is half the size. M1
Width of \( U_n \): \( 4 \times \left( \dfrac{1}{2} \right)^n = 4 \cdot 2^{-n} \). A1
[2 marks]
The side length of \( U_0 \) is 4 cm, and each successive square is half the size. M1
Width of \( U_n \): \( 4 \times \left( \dfrac{1}{2} \right)^n = 4 \cdot 2^{-n} \). A1
[2 marks]
(b)
Pixel width is 0.025 cm. Set \( 4 \cdot 2^{-n} > 0.025 \). A1
Solve: \( 2^{-n} > \dfrac{0.025}{4} = 0.00625 \), so \( 2^n < \dfrac{1}{0.00625} = 160 \).
Since \( 2^7 = 128 < 160 \) and \( 2^8 = 256 > 160 \), \( n \leq 7 \). A1
Number of squares: \( n = 0, 1, \ldots, 7 \), so 8 squares. A1
[3 marks]
Pixel width is 0.025 cm. Set \( 4 \cdot 2^{-n} > 0.025 \). A1
Solve: \( 2^{-n} > \dfrac{0.025}{4} = 0.00625 \), so \( 2^n < \dfrac{1}{0.00625} = 160 \).
Since \( 2^7 = 128 < 160 \) and \( 2^8 = 256 > 160 \), \( n \leq 7 \). A1
Number of squares: \( n = 0, 1, \ldots, 7 \), so 8 squares. A1
[3 marks]
(c)(i)
For \( U_1 \), scale factor is \( \dfrac{1}{2} \): \( \boldsymbol{A}_1 = \begin{pmatrix} \dfrac{1}{2} & 0 \\ 0 & \dfrac{1}{2} \end{pmatrix} \). A1
[1 mark]
For \( U_1 \), scale factor is \( \dfrac{1}{2} \): \( \boldsymbol{A}_1 = \begin{pmatrix} \dfrac{1}{2} & 0 \\ 0 & \dfrac{1}{2} \end{pmatrix} \). A1
[1 mark]
(c)(ii)
For \( U_n \), scale factor is \( \left( \dfrac{1}{2} \right)^n \): \( \boldsymbol{A}_n = \begin{pmatrix} \dfrac{1}{2^n} & 0 \\ 0 & \dfrac{1}{2^n} \end{pmatrix} \). A1
[1 mark]
For \( U_n \), scale factor is \( \left( \dfrac{1}{2} \right)^n \): \( \boldsymbol{A}_n = \begin{pmatrix} \dfrac{1}{2^n} & 0 \\ 0 & \dfrac{1}{2^n} \end{pmatrix} \). A1
[1 mark]
(d)(i)
Image of \( (0, 0) \) in \( U_1 \): \( (4, 4) \). A1
[1 mark]
Image of \( (0, 0) \) in \( U_1 \): \( (4, 4) \). A1
[1 mark]
(d)(ii)
Using \( \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} = \boldsymbol{A}_1 \begin{pmatrix} 0 \\ 0 \end{pmatrix} + \boldsymbol{b}_1 = \begin{pmatrix} 4 \\ 4 \end{pmatrix} \): M1
\( \boldsymbol{b}_1 = \begin{pmatrix} 4 \\ 4 \end{pmatrix} \). A1
[2 marks]
Using \( \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} = \boldsymbol{A}_1 \begin{pmatrix} 0 \\ 0 \end{pmatrix} + \boldsymbol{b}_1 = \begin{pmatrix} 4 \\ 4 \end{pmatrix} \): M1
\( \boldsymbol{b}_1 = \begin{pmatrix} 4 \\ 4 \end{pmatrix} \). A1
[2 marks]
(d)(iii)
Translation vector \( \boldsymbol{b}_n \) follows a geometric series: \( 4 + 2 + 1 + \cdots + \dfrac{4}{2^{n-1}} \). M1
Sum: \( 4 \left( 1 + \dfrac{1}{2} + \cdots + \dfrac{1}{2^{n-1}} \right) = 4 \cdot \dfrac{1 – \left( \dfrac{1}{2} \right)^n}{1 – \dfrac{1}{2}} = 8 \left( 1 – \dfrac{1}{2^n} \right) \). M1 A1
Thus, \( \boldsymbol{b}_n = \begin{pmatrix} 8 \left( 1 – 2^{-n} \right) \\ 8 \left( 1 – 2^{-n} \right) \end{pmatrix} \). AG
[3 marks]
Translation vector \( \boldsymbol{b}_n \) follows a geometric series: \( 4 + 2 + 1 + \cdots + \dfrac{4}{2^{n-1}} \). M1
Sum: \( 4 \left( 1 + \dfrac{1}{2} + \cdots + \dfrac{1}{2^{n-1}} \right) = 4 \cdot \dfrac{1 – \left( \dfrac{1}{2} \right)^n}{1 – \dfrac{1}{2}} = 8 \left( 1 – \dfrac{1}{2^n} \right) \). M1 A1
Thus, \( \boldsymbol{b}_n = \begin{pmatrix} 8 \left( 1 – 2^{-n} \right) \\ 8 \left( 1 – 2^{-n} \right) \end{pmatrix} \). AG
[3 marks]
(e)
Top left corner of \( U_0 \): \( (0, 4) \). Using \( \begin{pmatrix} x_7 \\ y_7 \end{pmatrix} = \boldsymbol{A}_7 \begin{pmatrix} 0 \\ 4 \end{pmatrix} + \boldsymbol{b}_7 \): M1
\( \boldsymbol{A}_7 = \begin{pmatrix} \dfrac{1}{2^7} & 0 \\ 0 & \dfrac{1}{2^7} \end{pmatrix} \), \( \boldsymbol{b}_7 = \begin{pmatrix} 8 \left( 1 – \dfrac{1}{2^7} \right) \\ 8 \left( 1 – \dfrac{1}{2^7} \right) \end{pmatrix} \). A1
Compute: \( \dfrac{4}{2^7} = \dfrac{4}{128} = 0.03125 \), \( 8 \left( 1 – \dfrac{1}{2^7} \right) = 8 \left( 1 – \dfrac{1}{128} \right) = 8 \cdot \dfrac{127}{128} = 7.9375 \).
Coordinates: \( (7.9375, 7.9375 + 0.03125) = (7.9375, 7.96875) \). A1
[3 marks]
Top left corner of \( U_0 \): \( (0, 4) \). Using \( \begin{pmatrix} x_7 \\ y_7 \end{pmatrix} = \boldsymbol{A}_7 \begin{pmatrix} 0 \\ 4 \end{pmatrix} + \boldsymbol{b}_7 \): M1
\( \boldsymbol{A}_7 = \begin{pmatrix} \dfrac{1}{2^7} & 0 \\ 0 & \dfrac{1}{2^7} \end{pmatrix} \), \( \boldsymbol{b}_7 = \begin{pmatrix} 8 \left( 1 – \dfrac{1}{2^7} \right) \\ 8 \left( 1 – \dfrac{1}{2^7} \right) \end{pmatrix} \). A1
Compute: \( \dfrac{4}{2^7} = \dfrac{4}{128} = 0.03125 \), \( 8 \left( 1 – \dfrac{1}{2^7} \right) = 8 \left( 1 – \dfrac{1}{128} \right) = 8 \cdot \dfrac{127}{128} = 7.9375 \).
Coordinates: \( (7.9375, 7.9375 + 0.03125) = (7.9375, 7.96875) \). A1
[3 marks]
(f)(i)
Scale factor \( s(\theta) = m \theta + c \). At \( \theta = 0 \), \( s = 1 \), so \( c = 1 \). M1 A1
At \( \theta = 360 \), \( s = \dfrac{1}{2} \), so \( \dfrac{1}{2} = 360 m + 1 \). A1
Solve: \( 360 m = -\dfrac{1}{2} \), \( m = -\dfrac{1}{720} \). Thus, \( s(\theta) = -\dfrac{\theta}{720} + 1 \). A1
[4 marks]
Scale factor \( s(\theta) = m \theta + c \). At \( \theta = 0 \), \( s = 1 \), so \( c = 1 \). M1 A1
At \( \theta = 360 \), \( s = \dfrac{1}{2} \), so \( \dfrac{1}{2} = 360 m + 1 \). A1
Solve: \( 360 m = -\dfrac{1}{2} \), \( m = -\dfrac{1}{720} \). Thus, \( s(\theta) = -\dfrac{\theta}{720} + 1 \). A1
[4 marks]
(f)(ii)
Enlargement matrix: \( E_\theta = \begin{pmatrix} -\dfrac{\theta}{720} + 1 & 0 \\ 0 & -\dfrac{\theta}{720} + 1 \end{pmatrix} \). A1
[1 mark]
Enlargement matrix: \( E_\theta = \begin{pmatrix} -\dfrac{\theta}{720} + 1 & 0 \\ 0 & -\dfrac{\theta}{720} + 1 \end{pmatrix} \). A1
[1 mark]
(f)(iii)
For \( \theta = 135^\circ \), \( s = -\dfrac{135}{720} + 1 = \dfrac{585}{720} = \dfrac{13}{16} \). Rotation matrix: \( \begin{pmatrix} \cos 135^\circ & -\sin 135^\circ \\ \sin 135^\circ & \cos 135^\circ \end{pmatrix} = \begin{pmatrix} -\dfrac{\sqrt{2}}{2} & -\dfrac{\sqrt{2}}{2} \\ \dfrac{\sqrt{2}}{2} & -\dfrac{\sqrt{2}}{2} \end{pmatrix} \). M1 A1
Combined: \( E_{135} \cdot \text{Rotation} = \dfrac{13}{16} \begin{pmatrix} -\dfrac{\sqrt{2}}{2} & -\dfrac{\sqrt{2}}{2} \\ \dfrac{\sqrt{2}}{2} & -\dfrac{\sqrt{2}}{2} \end{pmatrix} \). A1
Apply to \( (1, 1) \): \( \dfrac{13}{16} \begin{pmatrix} -\dfrac{\sqrt{2}}{2} & -\dfrac{\sqrt{2}}{2} \\ \dfrac{\sqrt{2}}{2} & -\dfrac{\sqrt{2}}{2} \end{pmatrix} \begin{pmatrix} 1 \\ 1 \end{pmatrix} = \dfrac{13}{16} \begin{pmatrix} -\sqrt{2} \\ 0 \end{pmatrix} \approx (-1.15, 0) \). A1
[4 marks]
For \( \theta = 135^\circ \), \( s = -\dfrac{135}{720} + 1 = \dfrac{585}{720} = \dfrac{13}{16} \). Rotation matrix: \( \begin{pmatrix} \cos 135^\circ & -\sin 135^\circ \\ \sin 135^\circ & \cos 135^\circ \end{pmatrix} = \begin{pmatrix} -\dfrac{\sqrt{2}}{2} & -\dfrac{\sqrt{2}}{2} \\ \dfrac{\sqrt{2}}{2} & -\dfrac{\sqrt{2}}{2} \end{pmatrix} \). M1 A1
Combined: \( E_{135} \cdot \text{Rotation} = \dfrac{13}{16} \begin{pmatrix} -\dfrac{\sqrt{2}}{2} & -\dfrac{\sqrt{2}}{2} \\ \dfrac{\sqrt{2}}{2} & -\dfrac{\sqrt{2}}{2} \end{pmatrix} \). A1
Apply to \( (1, 1) \): \( \dfrac{13}{16} \begin{pmatrix} -\dfrac{\sqrt{2}}{2} & -\dfrac{\sqrt{2}}{2} \\ \dfrac{\sqrt{2}}{2} & -\dfrac{\sqrt{2}}{2} \end{pmatrix} \begin{pmatrix} 1 \\ 1 \end{pmatrix} = \dfrac{13}{16} \begin{pmatrix} -\sqrt{2} \\ 0 \end{pmatrix} \approx (-1.15, 0) \). A1
[4 marks]
(g)
Set \( s(\theta) = -\dfrac{\theta}{720} + 1 = 0 \): \( \theta = 720^\circ \). A1
[1 mark]
Set \( s(\theta) = -\dfrac{\theta}{720} + 1 = 0 \): \( \theta = 720^\circ \). A1
[1 mark]
(h)
After \( \theta = 720^\circ \), the scale factor becomes negative and increases in magnitude, causing the image to expand from zero size in the opposite (third) quadrant. A1
It continues rotating counterclockwise for two revolutions (\( 720^\circ \)), ending in the third quadrant. A1
[2 marks]
After \( \theta = 720^\circ \), the scale factor becomes negative and increases in magnitude, causing the image to expand from zero size in the opposite (third) quadrant. A1
It continues rotating counterclockwise for two revolutions (\( 720^\circ \)), ending in the third quadrant. A1
[2 marks]
Total Marks: 22
