IBDP Physics- A.3 Work, energy and power- IB Style Questions For HL Paper 2 -FA 2025
Question
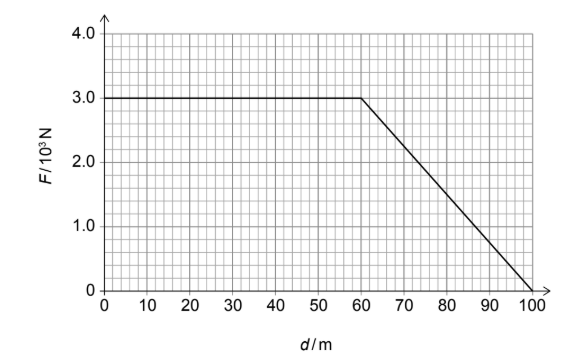
(ii) Calculate the final speed of the car.
Most-appropriate topic code (IB Physics):
▶️ Answer/Explanation
(a)
(i) The area under a force–distance graph represents the work done on the car, which is equal to the change in kinetic energy.
(ii) The total area under the graph is found by adding the areas of a rectangle and a triangle.
Area of rectangle \(= 3.0 \times 10^{3} \times 60 = 1.8 \times 10^{5}\,\text{J}\)
Area of triangle \(= \frac{1}{2} \times 3.0 \times 10^{3} \times (100 – 60) = 0.6 \times 10^{5}\,\text{J}\)
Total work done \(= 2.4 \times 10^{5}\,\text{J}\).
Using \(\frac{1}{2}mv^2 = 2.4 \times 10^{5}\):
\(v^2 = 300\)
\(v = \sqrt{300} \approx 17\,\text{m s}^{-1}\).
(b)
At constant speed, the driving force equals the resistive force. Since power \(P = Fv\):
\(F = \frac{140 \times 10^{3}}{45} \approx 3.11 \times 10^{3}\,\text{N}\).
Using \(F_d = cv^2\):
\(c = \frac{3.11 \times 10^{3}}{45^2} \approx 1.5\).
The unit of \(c\) is obtained from \(c = \frac{F}{v^2}\):
\( \frac{\text{kg m s}^{-2}}{\text{m}^2 \text{s}^{-2}} = \text{kg m}^{-1}\).
Answer: \(c = 1.5\,\text{kg m}^{-1}\).
