Home / B.3 Gas laws HL Paper 2- IBDP Physics 2025- Exam Style Questions

IBDP Physics- B.3 Gas laws- IB Style Questions For HL Paper 2 -FA 2025

IBDP Physics HL Paper 2 -FA 2025- All Chapters

Question

(a) Explain how thermal energy is transferred by the process of conduction.
The diagram illustrates a wall separating the interior of a room from the external surroundings. A heater maintains the room at a constant temperature.
The following information is provided:
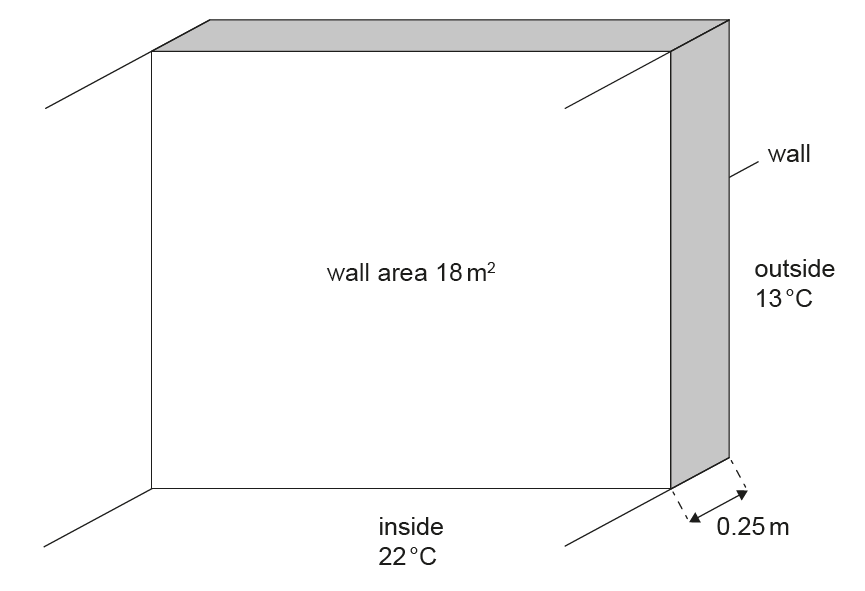
Thickness of the wall \(= 0.25\,m\)
Area of the wall \(= 18\,m^{2}\)
Thermal conductivity of the wall material \(= 1.3\,W\,m^{-1}\,K^{-1}\)
Constant temperature inside the room \(= 22^{\circ}C\)
Constant temperature outside \(= 13^{\circ}C\)
(b) Estimate the rate at which thermal energy is transferred out of the room through the wall, stating the answer with a suitable unit.
(c) During the night, the outside temperature drops below \(13^{\circ}C\). The heater is switched off at time \(t = 0\). The graph shows how the temperature \(T\) of the room varies with time \(t\).
(i) Explain why the magnitude of the gradient of the graph becomes smaller with time.
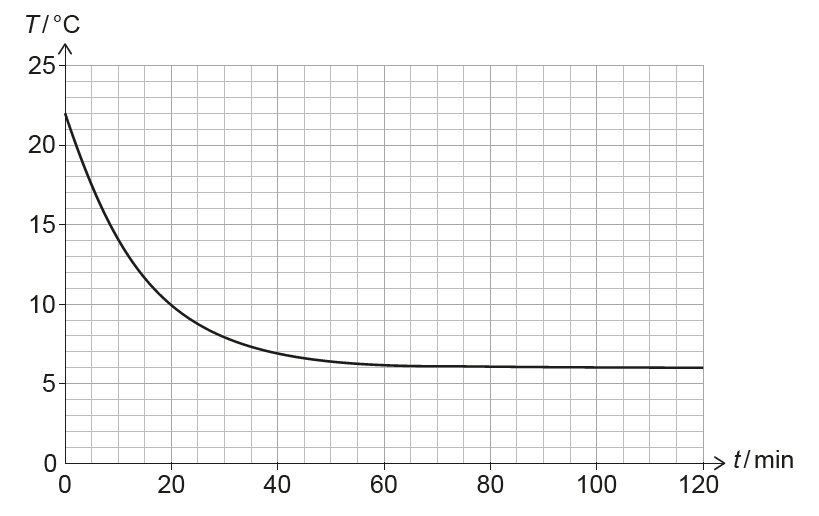
(ii) The pressure and volume of the air in the room remain constant, but the number of air molecules increases. Calculate the percentage increase in the number of air molecules in the room between \(t = 0\) and \(t = 120\,min\).
(d) Discuss how the second law of thermodynamics is illustrated by the cooling of the room.

Most-appropriate topic codes (IB Physics):

• Topic B.1: Thermal energy transfers (Conduction) — part (a), (b), (c)(i)
• Topic B.3: Gas laws — part (c)(ii)
• Topic B.4: Thermodynamics (Entropy / Second Law) — part (d)
▶️ Answer/Explanation
Detailed solution

(a)
In conduction, thermal energy is transferred through collisions between neighbouring atoms or molecules. In metals, free electrons also move through the material and transfer energy by collisions.

(b)
Using \(\dfrac{\Delta Q}{\Delta t} = kA\dfrac{\Delta T}{\Delta x}\):
\[ \text{Rate} = \frac{1.3 \times 18 \times (22 – 13)}{0.25} \approx 8.4 \times 10^{2}\,W \]

(c)
(i) The rate of heat transfer depends on the temperature difference between the room and the surroundings. As the room cools, this temperature difference becomes smaller, so the rate of cooling (the gradient) decreases.
(ii) From \(PV = NkT\), with \(P\) and \(V\) constant, \(NT = \text{constant}\).
At \(t=0\): \(T_1 = 22^\circ C = 295\,K\). At \(t=120\,min\): \(T_2 = 6^\circ C = 279\,K\).
\[ \frac{N_2}{N_1} = \frac{T_1}{T_2} = \frac{295}{279} \approx 1.057 \] Percentage increase \(\approx 5.7\%\).

(d)
Thermal energy flows naturally from the warmer room to the cooler surroundings. This process increases the total entropy of the universe, in accordance with the second law of thermodynamics.

More B.3 Gas laws HL Paper 2 Questions..
Scroll to Top