IBDP Physics- C.1 Simple harmonic motion- IB Style Questions For SL Paper 1A -FA 2025
Question
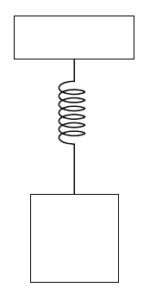
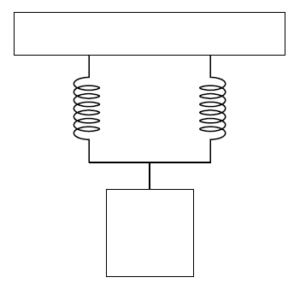
(B) \(\frac{1}{\sqrt{2}}\)
(C) \(\sqrt{2}\)
(D) 2
▶️ Answer/Explanation
1. Period of a Spring–Mass System:
\(T = 2\pi\sqrt{\frac{m}{k}}\).
2. Effect of Parallel Springs:
For two identical springs connected in parallel, the effective spring constant is \(k_{\text{eff}} = k + k = 2k\).
3. Compare the Time Periods:
- \(T_{1} = 2\pi\sqrt{\frac{m}{k}}\)
- \(T_{2} = 2\pi\sqrt{\frac{m}{2k}} = \frac{1}{\sqrt{2}}T_{1}\)
4. Ratio of Periods:
\(\frac{T_{2}}{T_{1}} = \frac{1}{\sqrt{2}}\).
✅ Answer: (B)
Question
| Option | Displacement | Velocity |
|---|---|---|
| A | positive maximum | zero |
| B | negative maximum | zero |
| C | positive maximum | negative maximum |
| D | negative maximum | negative maximum |
▶️Answer/Explanation
Question
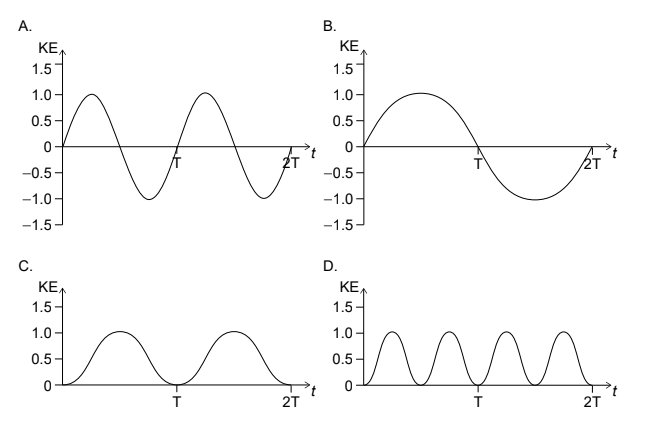
▶️ Answer/Explanation
In SHM, the velocity varies sinusoidally, for example \(v = v_{\max}\sin(\omega t + \phi)\).
The kinetic energy is \( \mathrm{KE} = \tfrac12 mv^2 \), so
\( \mathrm{KE} \propto \sin^2(\omega t + \phi) \).
Since \(\sin^2(\cdot)\) is always \(\ge 0\), the KE graph never goes negative.
Also, \(\sin^2(\omega t)\) has period \(\tfrac{\pi}{\omega} = \tfrac{T}{2}\), so over the time interval \(0 \to 2T\) there are \( \dfrac{2T}{T/2} = 4 \) identical “humps”.
Therefore the correct graph is the one that stays above zero and repeats every \(T/2\): Graph D.
✅ Answer: (D)
