Home / IBDP Physics- C.3 Wave phenomena- IB Style Questions For SL Paper 1A

IBDP Physics- C.3 Wave phenomena- IB Style Questions For SL Paper 1A -FA 2025

IBDP Physics SL Paper 1 -FA 2025- All Chapters

Question

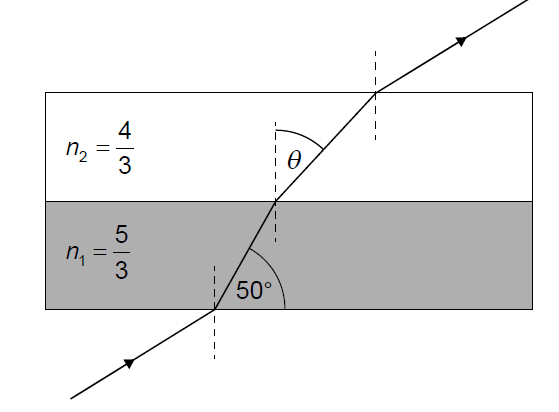
Light passes through two parallel layers as shown in figure below. The refractive indices for light travelling between air and the media are  \(n_{1}\) and \(n_{2}\). What is  angle \(\theta\) in image below?
(A) \(31^{\circ}\)
(B) \(38^{\circ}\)
(C) \(53^{\circ}\)
(D) \(73^{\circ}\)
▶️ Answer/Explanation
Detailed solution

1. Apply Snell’s Law at the Interface:
\(n_1 \sin \theta_1 = n_2 \sin \theta_2\)
Here, medium 1 is the bottom layer and medium 2 is the top layer.

  • \(n_1 = 5/3\)
  • \(\theta_1 = 50^{\circ}\) (angle of incidence with normal)
  • \(n_2 = 4/3\)
  • \(\theta_2 = \theta\) (angle of refraction)

2. Set up Equation:
\(\frac{5}{3} \sin 50^{\circ} = \frac{4}{3} \sin \theta\)

3. Solve:
Cancel the \(/3\):
\(5 \sin 50^{\circ} = 4 \sin \theta\)
\(\sin \theta = \frac{5}{4} \sin 50^{\circ}\)
\(\sin \theta \approx 1.25 \times 0.766 = 0.9575\)
\(\theta = \arcsin(0.9575) \approx 73.2^{\circ}\).
✅ Answer: (C)

Question

A group of students perform an experiment to find the refractive index of a glass block. They measure various values of the angle of incidence \(i\) and the angle of refraction \(r\) for a ray entering the glass from air. They plot a graph of \( \sin r \) against \( \sin i \).
C.3 Wave phenomena SL Paper 2
They determine the gradient of the graph to be \(m\).
Which of the following gives the critical angle of the glass?
(A) \( \sin^{-1}(m) \)
(B) \( \sin^{-1}\!\left(\dfrac{1}{m}\right) \)
(C) \( m \)
(D) \( \dfrac{1}{m} \)
▶️ Answer/Explanation
Detailed solution
Using Snell’s law for air to glass:
\(n_1 \sin i = n_2 \sin r\).
With \(n_1=1\) (air) and \(n_2=n\) (glass), \( \sin r = \dfrac{1}{n}\sin i \).
Therefore the gradient of the graph is \[ m=\frac{\sin r}{\sin i}=\frac{1}{n} \] so \(n=\dfrac{1}{m}\).
Total internal reflection occurs for a ray going from glass (denser) to air (rarer). At the critical angle \(\theta_c\), the refracted angle is \(90^\circ\), so \[ n\sin\theta_c = 1\cdot \sin 90^\circ = 1 \;\Rightarrow\; \sin\theta_c=\frac{1}{n}. \]
Since \(\dfrac{1}{n}=m\), we get \[ \theta_c=\sin^{-1}(m). \]

✅ Answer: (A)

Question

Two identical sources oscillate in phase and produce constructive interference at a point \(P\). The intensity recorded at \(P\) is \(I\).
What is the intensity at \(P\) from one source?
(A) \(\sqrt{2}\,I\)
(B) \(I\)
(C) \(\dfrac{I}{2}\)
(D) \(\dfrac{I}{4}\)
▶️ Answer/Explanation
Detailed solution

For two identical coherent sources oscillating in phase, the wave amplitudes add at a point of constructive interference.

Let the intensity at \(P\) due to one source be \(I_1\).
Intensity is proportional to the square of amplitude: \(I \propto A^2\).

With two sources in phase, the resultant amplitude is doubled: \(A_{\text{total}} = 2A\).
Hence the resultant intensity is \[ I_{\text{total}} \propto (2A)^2 = 4A^2. \] So \(I_{\text{total}} = 4I_1\).

Given \(I_{\text{total}} = I\), we have \(I_1 = \dfrac{I}{4}\).

✅ Answer: (D)

More C.3 Wave phenomena SL Paper 1 Questions..
Scroll to Top