Home / IBDP Physics- C.5 Doppler effect- IB Style Questions For HL Paper 2

IBDP Physics- C.5 Doppler effect- IB Style Questions For HL Paper 2 -FA 2025

IBDP Physics HL Paper 2 -FA 2025- All Chapters

Question

(a) A sound detector travels along a straight line joining it to a stationary loudspeaker. The loudspeaker emits sound waves of frequency \(1700\,Hz\). The speed of sound in air is \(340\,m\,s^{-1}\). The frequency measured by the detector is \(1600\,Hz\).
(i) State the direction in which the detector is moving.
(ii) Calculate the speed of the detector.
(b) The loudspeaker and the detector are now fixed in position above a water surface. The loudspeaker is at point L and the detector at point D, with L and D at the same height above the water. Sound reaches D by two paths: the direct path LD and the reflected path LPD.
The following information is provided:
Frequency of the sound wave \(= 1700\,Hz\)
Speed of sound in air \(= 340\,m\,s^{-1}\)
Speed of sound in water \(= 1500\,m\,s^{-1}\)
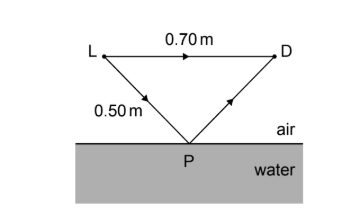
Distance \(LD = 0.70\,m\)
Distance \(LP = 0.50\,m\)
(i) Calculate the wavelength of the sound wave in air.
(ii) Explain why the sound arriving at D undergoes destructive interference.
(c) Predict whether the sound wave is able to enter the water at point P.

Most-appropriate topic codes (IB Physics):

• Topic C.5: Doppler effect — part (a)
• Topic C.3: Wave phenomena (interference, refraction) — parts (b) and (c)
▶️ Answer/Explanation
Detailed solution

(a)
(i) The detected frequency (\(1600\,Hz\)) is lower than the emitted frequency (\(1700\,Hz\)), indicating that the detector is moving away from the loudspeaker.
(ii) Using the Doppler equation for a moving observer, \[ f’ = f\left(\frac{v – u_o}{v}\right) \] \[ 1600 = 1700\left(\frac{340 – u_o}{340}\right) \] \[ u_o = 20\,m\,s^{-1}. \]

(b)
(i) The wavelength in air is \[ \lambda = \frac{v}{f} = \frac{340}{1700} = 0.20\,m. \] (ii) The reflected path length is \(LP + PD = 0.50 + 0.50 = 1.00\,m\), while the direct path length is \(0.70\,m\). The path difference is therefore \(0.30\,m\). Since \(\frac{0.30}{0.20} = 1.5\lambda\), the waves arrive at D out of phase, resulting in destructive interference.

(c)
At point P, the angle of incidence is approximately \(44^\circ\). Sound travels much faster in water than in air. Applying Snell’s law shows that refraction would require \(\sin\theta_r > 1\), which is not possible. Therefore, the sound undergoes total internal reflection and cannot enter the water.

More DP Physics HL Paper 2 Questions..
Scroll to Top