Home / IBDP Physics- C.5 Doppler Effect- IB Style Questions For SL Paper 1A

IBDP Physics- C.5 Doppler Effect- IB Style Questions For SL Paper 1A -FA 2025

IBDP Physics SL Paper 1 -FA 2025- All Chapters

Question

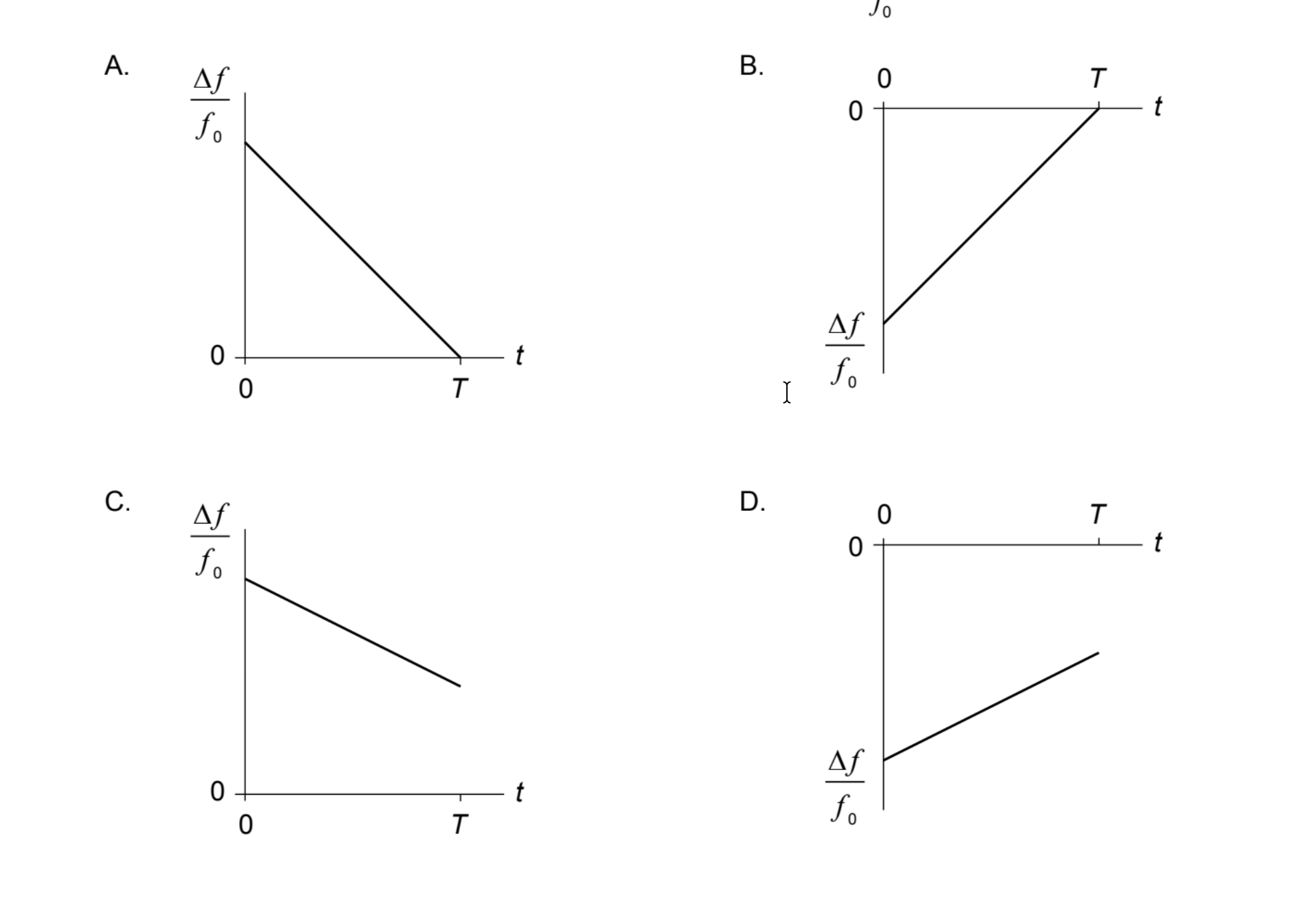
A sound source emitting waves of frequency \(f_{0}\) moves towards a stationary observer. At time \(t=0\), the source starts to slow down and comes to rest at \(t=T\), without ever passing the observer. The speed of the source remains much smaller than the speed of sound throughout. How does the relative frequency change \(\frac{\Delta f}{f_{0}}\) of the sound detected by the observer vary with time \(t\)?
 
▶️ Answer/Explanation
Detailed solution

1. Doppler Effect Formula:
\(\frac{\Delta f}{f_0} \approx \frac{v}{c}\) where \(v\) is the source velocity and \(c\) is the speed of sound.
Because the source is approaching, the observed frequency is increased (\(\Delta f > 0\)).

2. Analyze Motion:
The source slows down until it comes to rest.
At \(t=0\), the velocity \(v\) is greatest, so \(\frac{\Delta f}{f_0}\) is at its maximum positive value.
At \(t=T\), the velocity is zero, so \(\frac{\Delta f}{f_0} = 0\).
With uniform deceleration, the velocity — and hence \(\frac{\Delta f}{f_0}\) — decreases linearly with time.

3. Match Graph:
The correct graph begins at a positive value and decreases linearly to zero at \(t=T\).
Graph A satisfies these conditions.
✅ Answer: (A)

Question

A radar speed detector is used to measure the speed of a car. The car moves towards the detector with speed \(v\)

The detector emits microwaves of frequency \(f\) and speed \(c\). Which of the following is the change in frequency of the microwaves measured at the detector after reflection by the car?
(A) \(-\dfrac{2vf}{c}\)
(B) \(-\dfrac{vf}{c}\)
(C) \(\dfrac{vf}{c}\)
(D) \(\dfrac{2vf}{c}\)
▶️ Answer/Explanation
Detailed solution
First Doppler shift (car as moving observer):
Frequency received by the car:
\(f’ \approx f\left(1+\dfrac{v}{c}\right)\)
Second Doppler shift (reflected wave back to detector):
The reflected wave is Doppler shifted again on the return trip, so the detector receives:
\(f” \approx f’\left(1+\dfrac{v}{c}\right)\)
Hence,
\(f” \approx f\left(1+\dfrac{v}{c}\right)\left(1+\dfrac{v}{c}\right) = f\left(1+\dfrac{v}{c}\right)^2\)
For \(v \ll c\), use \((1+x)^2 \approx 1+2x\):
\(f” \approx f\left(1+\dfrac{2v}{c}\right)\)
Therefore the change in frequency is
\(\Delta f = f”-f \approx f\dfrac{2v}{c} = \dfrac{2vf}{c}\)

✅ Answer: (D)

Question

A fire engine with its siren sounding approaches and then passes a stationary observer. The frequency of the sound emitted by the siren is \(f_s\). The frequency of the sound measured by the observer is \(f_o\). Which of the following describes the relationship between \(f_o\) and \(f_s\)?
\[ \begin{array}{|c|c|c|} \hline \textbf{Option} & \textbf{Fire engine approaching observer} & \textbf{Fire engine moving away from observer} \\ \hline \text{A} & f_o > f_s & f_o < f_s \\ \hline \text{B} & f_o < f_s & f_o < f_s \\ \hline \text{C} & f_o > f_s & f_o > f_s \\ \hline \text{D} & f_o < f_s & f_o > f_s \\ \hline \end{array} \]
▶️ Answer/Explanation
Detailed solution

When a sound source moves towards a stationary observer, the wavefronts reach the observer more frequently. As a result, the observed frequency is higher than the source frequency: \(f_o > f_s\).

After the fire engine passes the observer and moves away, the wavefronts reach the observer less frequently. Hence, the observed frequency becomes lower than the source frequency: \(f_o < f_s\).

This corresponds to option A in the table.

✅ Answer: (A)

More C.5 Doppler Effect SL Paper 1 Questions..
Scroll to Top