IBDP Physics- E.2 Quantum physics- IB Style Questions For HL Paper 2 -FA 2025
Question
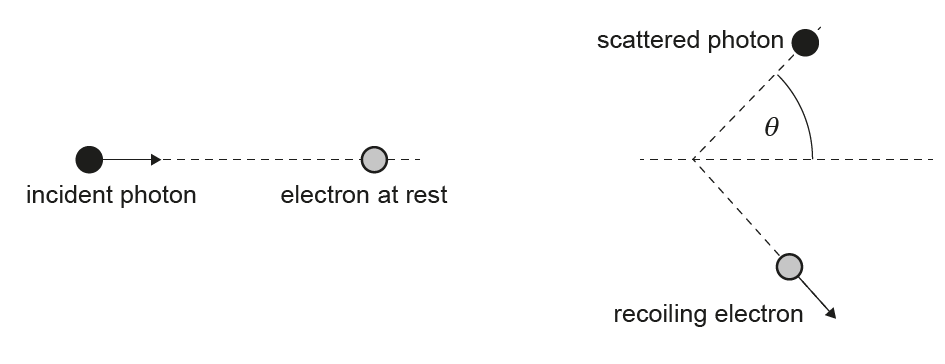
(ii) Calculate the kinetic energy of the recoiling electron.
(iii) For an electron, \(\frac{h}{m_{e}c}=2.43\times10^{-12}\,m\). Determine the value of \(\theta\).
Most-appropriate topic codes (IB Physics):
▶️ Answer/Explanation
(a)
In Compton scattering, a photon collides with an electron and the interaction can be treated as a particle-like collision in which momentum is exchanged. The measurable change in the photon’s wavelength (and hence momentum) is direct evidence of photon momentum.
The photoelectric effect shows that light energy is quantized, but it does not as directly demonstrate a momentum-exchange “collision” between light and a particle.
(b)
During the scattering, the photon transfers some of its energy to the electron (the electron gains kinetic energy). The scattered photon therefore has lower energy than the incident photon. Since \(E=\frac{hc}{\lambda}\), a decrease in photon energy implies an increase in wavelength, so the scattered wavelength is longer.
(c)
(i)
Using \(E=\frac{hc}{\lambda}\) and \(hc \approx 1.24\times10^{-6}\,eV\,m\):
\(E_s=\frac{1.24\times10^{-6}}{7.47\times10^{-12}}\,eV \approx 1.66\times10^{5}\,eV = 0.166\,MeV \approx 0.17\,MeV.\)
(ii)
By energy conservation (electron initially at rest):
\(K_e = E_i – E_s = 0.194\,MeV – 0.166\,MeV = 0.028\,MeV.\)
(iii)
Compton shift: \(\Delta\lambda=\lambda_s-\lambda_i=\frac{h}{m_ec}(1-\cos\theta)\).
\(\Delta\lambda=(7.47-6.40)\times10^{-12}\,m = 1.07\times10^{-12}\,m.\)
\(1.07\times10^{-12} = (2.43\times10^{-12})(1-\cos\theta)\)
\(1-\cos\theta = \frac{1.07}{2.43}\approx 0.44\)
\(\cos\theta \approx 0.56 \Rightarrow \theta \approx 56^\circ\) (about \(0.98\,rad\)).
