Internal energy IB DP Physics Study Notes - 2025 Syllabus

Internal energy IB DP Physics Study Notes

Internal energy IB DP Physics Study Notes at IITian Academy focus on specific topic and type of questions asked in actual exam. Study Notes focus on IB Physics syllabus with Students should understand

The change in internal energy, as given by \( \Delta U = \frac{3}{2} Nk_B \Delta T = \frac{3}{2} nR\Delta T \), of a system is related to the change in its temperature.
Entropy (\( S \)) is a thermodynamic quantity that relates to the degree of disorder of the particles in a system.
Entropy can be determined in terms of macroscopic quantities, such as thermal energy and temperature, as given by \( \Delta S = \frac{\Delta Q}{T} \), and also in terms of the properties of individual particles of the system as given by \( S = k_B \ln \Omega \), where \( k_B \) is the Boltzmann constant and \( \Omega \) is the number of possible microstates of the system.

Standard level and higher level: There is no Standard level content
Additional higher level: 8 hours

IB DP Physics 2025 -Study Notes -All Topics

Internal Energy

Materials have internal energy, \( U \).
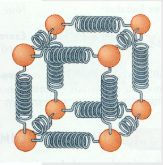
This is the KE of random motions of atoms + PE due to forces between atoms.
Can be modeled as vibrating springs joining atoms to each other in solids or within molecules.
\( U \) is the sum of all KE and PE of atoms/molecules in the material. \( \Delta U \) is the change of internal energy.
If \( \Delta U > 0 \), then its the “systems” internal energy which is being increased
If \( \Delta U < 0 \), then its the “systems” internal energy which is being decreased.

FYI:

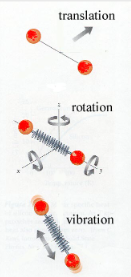
In polyatomic gases, the molecules can store energy in rotations and vibrations in addition to translations. This adds more degrees of freedom, increasing internal energy at a given temperature. As a result, complex gases warm up more slowly.

Without proof, for each degree of freedom, energy stored is:

\( \text{Energy} = \frac{1}{2} k_b T \)

In 3D space, there are 3 translational degrees of freedom. So for an ideal gas with \( N \) particles:

\( U = \frac{3}{2} N k_b T \)

Hence, \( U \propto T \)

\( \Delta U = \frac{3}{2} N k_b \Delta T = \frac{3}{2} n R \Delta T \)

Example:

An ideal monatomic gas contains \( 2.0 \, \text{mol} \) of particles. If its temperature rises from \( 300 \, \text{K} \) to \( 500 \, \text{K} \), calculate the increase in internal energy.

▶️ Answer/Explanation

Use: \( \Delta U = \frac{3}{2} n R \Delta T \)

Here, \( n = 2.0 \), \( R = 8.31 \, \text{J·mol}^{-1} \text{K}^{-1} \), \( \Delta T = 200 \, \text{K} \)

\( \Delta U = \frac{3}{2} \cdot 2.0 \cdot 8.31 \cdot 200 = \boxed{4986 \, \text{J}} \)

The internal energy of the gas increases by 4986 J.

Microstates

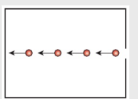
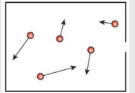
To better understand entropy, we need to consider the idea of microstates. Let’s start by considering 2 states, speed and direction.
Each of the possible speeds would be a microstate. Likewise each of the possible directions would be a microstate.
Since the particles here can only travel in one direction with one speed, they have few microstates and low entropy.
In this example, the particles have more speed microstates and more directions microstates, meaning that they also have greater entropy.

Entropy calculations using microstates

We use the symbol \( \Omega \) to represent the number of microstates of particles in a system. Since microstates can be the number of particles, directions, speeds, and positions, \( \Omega \) can be a very large number, so we use \( \ln \Omega \) instead.
To calculate the entropy of a system of particles:
Where \( S \) is the entropy value in \( \text{J K}^{-1} \) and \( k_B \) is Stephan-Boltzmann’s constant.

EXAMPLE:

What is the entropy of a system of gas particles, which has \( 1 \times 10^{22} \) microstates?

▶️Answer/Explanation

SOLUTION:

\[
S = k_B \ln \Omega = (1.38 \times 10^{-23}) \ln (1 \times 10^{22}) = 7.0 \times 10^{-22} \, \text{J K}^{-1}
\]

Changes in Entropy

While the previous calculation works, it is often not practical as measuring microstates is difficult.
However, using the properties of internal energy and temperature, we can more easily measure changes in entropy
Again ΔS has the units J K^-1. Remember that temperature is always in Kelvin.
Since we are often looking at the entropy change, this formula proves to be very useful in looking at entropy problems.

Example:

Calculate the change in entropy when 100 J of thermal energy is transferred to a system at a constant temperature of 300 K.

▶️ Answer/Explanation

Formula:

\( \Delta S = \frac{Q}{T} \)

Substitute:

\( \Delta S = \frac{100 \, \text{J}}{300 \, \text{K}} = \boxed{0.33 \, \text{J·K}^{-1}} \)

The system’s entropy increases by 0.33 J·K^-1.

Internal energy IB DP Physics Study Notes - 2025 Syllabus