IBDP Chemistry - Structure 1.5 Ideal gases- IB Style Questions For SL Paper 1A - FA 2025
Question
| Gas | Pressure | Temperature | |
| A | Phosphine, \(PH_{3}\) | Low | High |
| B | Ammonia, \(NH_{3}\) | Low | High |
| C | Phosphine, \(PH_{3}\) | High | Low |
| D | Ammonia, \(NH_{3}\) | High | Low |
▶️ Answer/Explanation
1. Ideal Gas Conditions:
Gases behave most ideally at low pressure (negligible volume of particles) and high temperature (negligible intermolecular forces). This eliminates options C and D.
2. Intermolecular Forces:
To deviate the least, the gas should have the weakest intermolecular forces.
- Ammonia (\(NH_{3}\)): Exhibits hydrogen bonding (strong).
- Phosphine (\(PH_{3}\)): Exhibits dipole-dipole forces and London dispersion forces, but no hydrogen bonding (P is not electronegative enough).
Since \(PH_{3}\) has weaker intermolecular forces than \(NH_{3}\), it will behave more ideally.
3. Conclusion:
\(PH_{3}\) at Low Pressure and High Temperature.
✅ Answer: (A)
Question
| Mass of gas | \(40.0\ \text{g}\) |
| Volume | \(220\ \text{cm}^3\) |
| Temperature | \(17^{\circ}\text{C}\) |
| Pressure | \(98\ \text{kPa}\) |
▶️ Answer/Explanation
For an ideal gas: \[ pV = nRT \] so the number of moles is \[ n = \frac{pV}{RT}. \]
The molar mass \(M\) is \[ M = \frac{\text{mass}}{n} = \frac{m}{pV/(RT)} = \frac{mRT}{pV}. \]
Convert the data: \(T = 17^{\circ}\text{C} = 290\ \text{K}\), \(V = 220\ \text{cm}^3 = 0.220\ \text{dm}^3\) (unit-compatible with \(p = 98\ \text{kPa}\)).
Substitute into \(M = \dfrac{mRT}{pV}\): \[ M = \frac{40.0 \times 8.31 \times 290}{98 \times 0.220}, \] which corresponds to option A.
✅ Answer: (A)
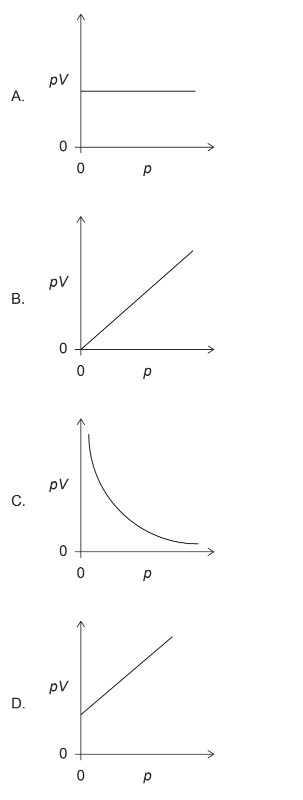
Question
▶️ Answer/Explanation
For an ideal gas: \[ pV = nRT \] where \(n\) is the number of moles, \(R\) is the gas constant and \(T\) is the temperature.
In this experiment the mass of gas is fixed (\(n\) constant) and the temperature is constant (\(T\) constant), so \[ pV = \text{constant}. \]
A plot of \(pV\) against \(p\) must therefore be a horizontal line, showing that \(pV\) does not change as \(p\) varies. This corresponds to option A.
✅ Answer: (A)