IBDP Physics HL Paper 1B- Data-Based Question- New Syllabus

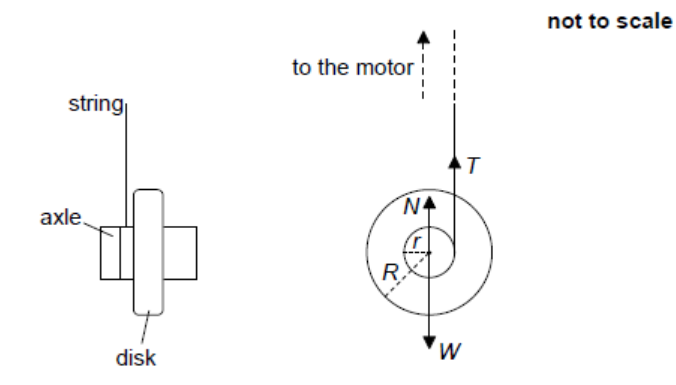
(a)
The line of action of the weight passes through the axis of rotation, so it produces no turning effect.
\( \boxed{0\,\text{N m}} \)

(b)(i)
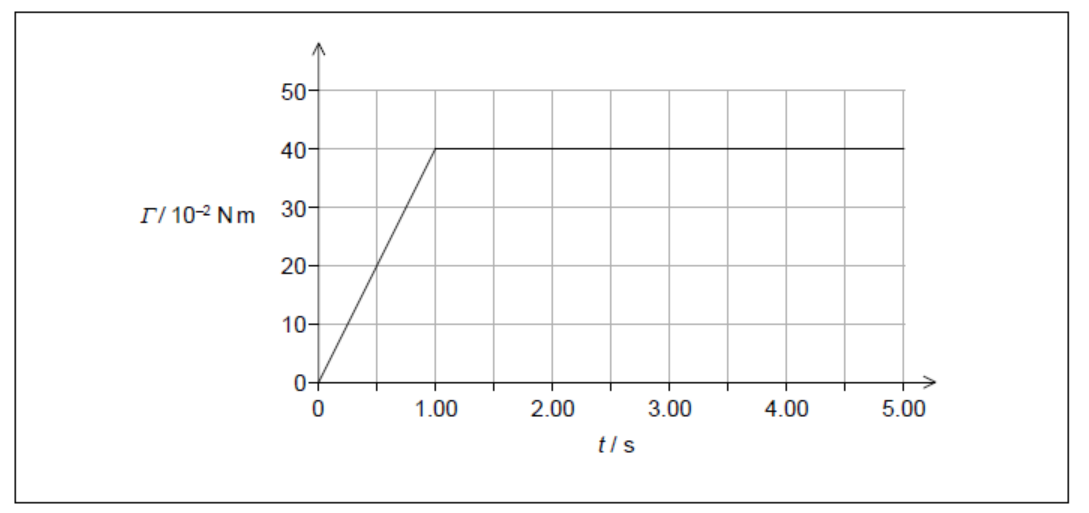
The area under a torque–time graph represents the change in angular momentum (angular impulse).

(b)(ii)
Area under the graph \(= \Delta L = 1.80\,\text{kg m}^2\text{s}^{-1}\).
Using \( \Delta L = I\omega \):
\( 1.80 = \left(\frac{1}{2} \times 5.00 \times 0.060^2\right)\omega \)
\( \omega = 200\,\text{rad s}^{-1} \).

(b)(iii)
Maximum torque \( \Gamma_{\max} = Tr \).
\( T = \dfrac{0.40}{0.012} = 33.3\,\text{N} \).

(c)(i)
Translational equilibrium occurs when the resultant force on a body is zero.
Rotational equilibrium occurs when the resultant torque on a body is zero.

(c)(ii)
The angular displacement before stopping is \( \theta = 2\pi \times 8000 \).
Using \( 0 = \omega^2 + 2\alpha\theta \):
\( \alpha = -0.398\,\text{rad s}^{-2} \).
Frictional torque: \( \tau = I\alpha = 0.398 \times \left(\frac{1}{2} \times 5.00 \times 0.060^2\right) \).
\( \boxed{3.58 \times 10^{-3}\,\text{N m}} \).