IBDP Physics- A.1 Kinematics- IB Style Questions For SL Paper 1A -FA 2025

Question

A stone is released from rest and falls vertically. Air resistance is negligible. What is correct about the stone during each consecutive second of its motion?

(A) The change in velocity is constant.
(B) The change in displacement is constant.
(C) The change in acceleration decreases.
(D) The change in speed increases.

▶️ Answer/Explanation

Correct Answer: \( \boxed{\mathrm{A}} \)

The stone is in free fall, so it has a constant acceleration due to gravity:

\(a=g\)

Acceleration is the rate of change of velocity:

\(a=\frac{\Delta v}{\Delta t}\)

Since \(g\) is constant, the velocity changes by the same amount during every equal time interval.

For each consecutive \(1\,\mathrm{s}\) interval,

\(\Delta v=g(1)=g\)

Therefore, the change in velocity is constant.

The displacement during each second is not constant because the speed increases continuously.

Hence, the correct answer is \( \boxed{\mathrm{A}} \).

Question

A projectile is launched horizontally from the top of a cliff with a speed of \(10\,\mathrm{m\,s^{-1}}\). The projectile hits the ground at a distance of \(30\,\mathrm{m}\) from the base of the cliff. Air resistance is negligible.

What is the height of the cliff?

(A) \(15\,\mathrm{m}\)
(B) \(30\,\mathrm{m}\)
(C) \(45\,\mathrm{m}\)
(D) \(90\,\mathrm{m}\)

▶️ Answer/Explanation

Correct Answer: \( \boxed{\mathrm{C}} \)

The horizontal motion is at constant velocity because there is no horizontal acceleration.

Using

\(x=v_xt\)

we find the time of flight:

\(30=10t\)

\(t=3.0\,\mathrm{s}\)

The initial vertical velocity is zero. Therefore, the vertical displacement is

\(y=u_yt+\frac{1}{2}gt^2\)

Since \(u_y=0\),

\(y=\frac{1}{2}gt^2\)

Taking \(g=10\,\mathrm{m\,s^{-2}}\),

\(y=\frac{1}{2}(10)(3)^2\)

\(y=45\,\mathrm{m}\)

Thus, the height of the cliff is

\( \boxed{45\,\mathrm{m}} \)

Hence, the correct answer is \( \boxed{\mathrm{C}} \).

Question

A car travels clockwise around a circular track of radius \(R\). What is the magnitude of displacement from \(X\) to \(Y\)?

(A) \(R \dfrac{3\pi}{2}\)
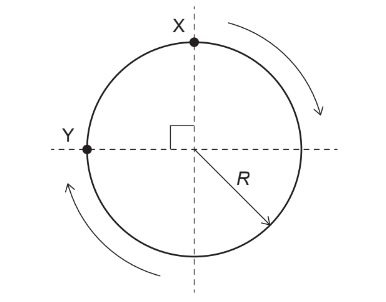
(B) \(R \dfrac{\pi}{2}\)
(C) \(R\sqrt{2}\)
(D) \(R\)

▶️ Answer/Explanation

Detailed solution

The displacement from \(X\) to \(Y\) is the straight-line distance (the chord), not the distance travelled along the track.

From the diagram, \(X\) and \(Y\) are \(90^\circ\) apart around the circle, so the radii to \(X\) and \(Y\) are perpendicular. This forms a right-angled triangle with legs \(R\) and \(R\).
Therefore, the displacement magnitude is
\(XY = \sqrt{R^2 + R^2} = R\sqrt{2}\).

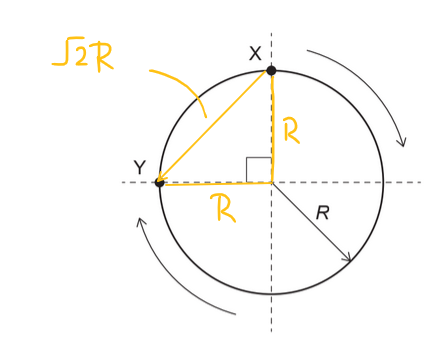
✅ Answer: (C)

IBDP Physics- A.1 Kinematics- IB Style Questions For SL Paper 1A -FA 2025

Question

Question

Question

Resources

Members

Company