Home / IB DP / IB Physics 2026, 2027 & 2028 / IB Physics SL / IBDP Physics- B.2 Greenhouse effect- IB Style Questions For SL Paper 1A

IBDP Physics- B.2 Greenhouse effect- IB Style Questions For SL Paper 1A -FA 2025

IBDP Physics SL Paper 1 -FA 2025- All Chapters

Question

Which of the following is primary cause of the enhanced greenhouse effect?
(A) Melting of ice at Earth’s poles
(B) Increases in volcanic activity
(C) Deforestation of rain forests
(D) Burning of fossil fuels
▶️ Answer/Explanation
Detailed solution

1. Definition:
The enhanced greenhouse effect refers to the additional warming of the Earth caused by human activities increasing the concentration of greenhouse gases.

2. Evaluate Options:

  • (A) Melting ice is an effect/feedback loop, not a primary cause.
  • (B) Volcanic activity is a natural cause, not the primary driver of the enhanced effect.
  • (C) Deforestation contributes, but less than fossil fuels.
  • (D) Burning fossil fuels releases massive amounts of \(CO_2\), which is the most significant contributor to the enhanced effect.

✅ Answer: (D)

Question

Light of intensity \(500\,\text{W m}^{-2}\) is incident on concrete and on snow. \(300\,\text{W m}^{-2}\) is reflected from the concrete and \(400\,\text{W m}^{-2}\) is reflected from the snow.
What is \(\dfrac{\text{albedo of concrete}}{\text{albedo of snow}}\)?
A. \(\dfrac{1}{2}\)
B. \(\dfrac{3}{4}\)
C. \(\dfrac{4}{3}\)
D. \(2\)
▶️ Answer / Explanation

Albedo is the ratio of reflected intensity to incident intensity:
\[ \alpha = \frac{I_{\text{reflected}}}{I_{\text{incident}}} \]
For concrete:
\[ \alpha_{\text{concrete}}=\frac{300}{500}=0.6 \]
For snow:
\[ \alpha_{\text{snow}}=\frac{400}{500}=0.8 \]
Therefore,
\[ \frac{\alpha_{\text{concrete}}}{\alpha_{\text{snow}}} = \frac{0.6}{0.8} = \frac{6}{8} = \frac{3}{4} \]

✅ Answer: B

Question

A planet has an albedo of \(0.30\). A simplified energy balance for the planet is shown.
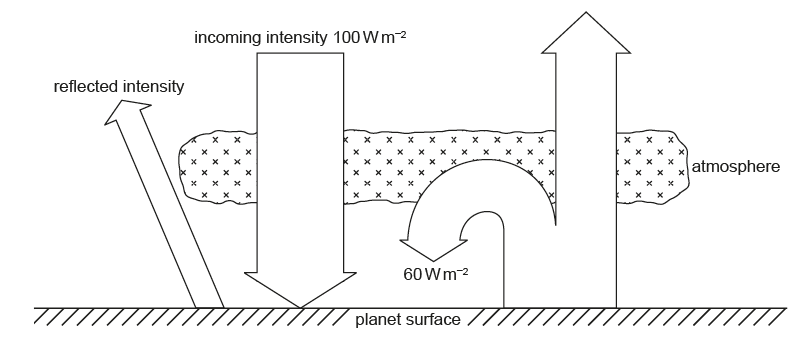
B.2 Greenhouse effect SL Paper 1
What is the intensity radiated by the surface of the planet?
A. \(70\,\text{W m}^{-2}\)
B. \(90\,\text{W m}^{-2}\)
C. \(100\,\text{W m}^{-2}\)
D. \(130\,\text{W m}^{-2}\)
▶️ Answer / Explanation
Incoming intensity is \(100\,\text{W m}^{-2}\). Albedo \(=0.30\), so the absorbed intensity is
\[ I_{\text{absorbed}} = (1-0.30)\times 100 = 0.70\times 100 = 70\,\text{W m}^{-2}. \]
The atmosphere radiates back to the surface \(60\,\text{W m}^{-2}\).

At equilibrium, the surface must radiate the total energy it receives:
\[ I_{\text{surface}} = I_{\text{absorbed}} + I_{\text{back radiation}} = 70 + 60 = 130\,\text{W m}^{-2}. \]

✅ Answer: D
More B.2 Greenhouse effect SL Paper 1 Questions..
Scroll to Top