Question
Pip and Ali share $785 in the ratio Pip:Ali = 4 :1.
Work out Pip’s share.
▶️Answer/Explanation
To work out Pip’s share, we need to calculate the fraction of the total amount that corresponds to Pip’s ratio.
The total ratio is 4 + 1 = 5.
Pip’s fraction of the total amount can be calculated as:
Pip’s fraction = (Pip’s ratio / Total ratio) × Total amount
Pip’s fraction\(=\frac{4}{5}785\)
Pip’s share \(= \frac{4}{5}785\)
Pip’s share ≈\( $628\)
Therefore, Pip’s share is approximately\( $628.\)
Question
Ravi cycles from home to the bank.
It takes him 15 minutes, cycling at a constant speed of 14km/h.
(a) Work out how far Ravi cycles from home to the bank.
(b) Ravi stays at the bank for 18 minutes.
He then cycles home at a constant speed for 12 minutes.
Draw the travel graph to show Ravi’s journey since he left home.
▶️Answer/Explanation
(a) To work out the distance Ravi cycles from home to the bank, we can use the formula:
Distance = Speed × Time
Ravi’s speed is 14 km/h and the time it takes him is 15 minutes. However, we need to convert the time from minutes to hours to match the speed unit.
15 minutes\(=\frac{15}{60}hours \)= 0.25 hours
Distance \(= 14 kmh^{-1}\times 0.25\) hours
Distance = 3.5 km
Therefore, Ravi cycles a distance of 3.5 km from home to the bank.
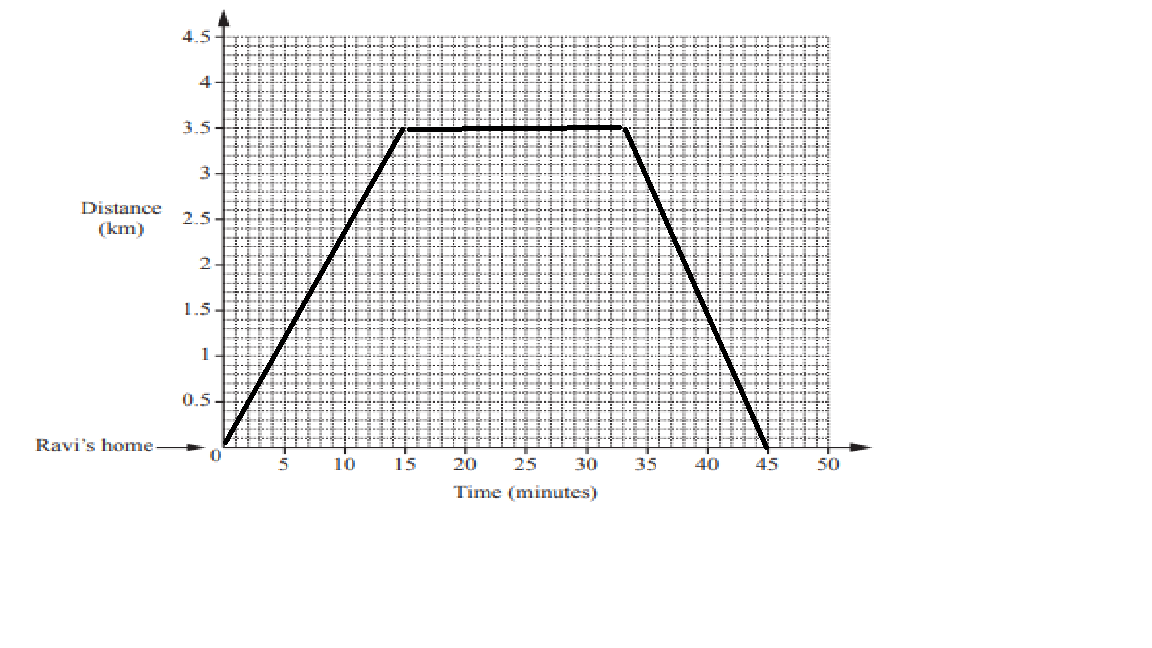
(b) To draw the travel graph to show Ravi’s journey, we can use a distance-time graph.
Let’s assume the x-axis represents time in minutes and the y-axis represents distance in kilometers.
Starting from the origin (0, 0), we plot the following points:
– At time 0 minutes, the distance is 0 km (starting point).
– At time 15 minutes, the distance is 3.5 km (reached the bank).
– At time 33 minutes (15 minutes + 18 minutes), the distance is still 3.5 km (Ravi stays at the bank).
– At time 45 minutes (33 minutes + 12 minutes), the distance is 0 km (reached home).
The graph would have a straight line segment from (0, 0) to (15, 3.5) representing Ravi’s journey from home to the bank. Then, a horizontal line segment from (15, 3.5) to (33, 3.5) representing his stay at the bank. Finally, another straight line segment from (33, 3.5) to (45, 0) representing his journey back home.
The travel graph would look like this:
Question
Ahmed, Batuk and Chand share $1000 in the ratio 8:7:5.
Calculate the amount each receives.
▶️Answer/Explanation
To calculate the amount each person receives, we need to divide the total amount of $1000 in the given ratio of 8:7:5.
First, we need to find the total parts in the ratio:
8 + 7 + 5 = 20
Next, we can calculate the amount each person receives by multiplying their respective ratio parts with the total amount:
Ahmed’s share:
Amount \(=\frac{8}{20}\times 1000\)
Amount\( = $400\)
Batuk’s share:
Amount \(=\frac{7}{20}\times 1000\)
Amount =\( $350\)
Chand’s share:
Amount \(=\frac{5}{20}\times 1000\)
Amount \(= $250\)
Therefore, Ahmed receives \($400\), Batuk receives \($350\), and Chand receives \($250.\)
Question
Divide 120 in the ratio 1 : 2.
▶️Answer/Explanation
To divide 120 in the ratio 1:2, we need to determine the amount each part represents.
In this ratio, the total number of parts is 1 + 2 = 3.
To find the value of each part, we divide 120 by the total number of parts:
Value of each part =\frac{120}{3}= 40.
Now, we can calculate the amounts for each part based on the ratio:
First part: 1\times 40 = 40.
Second part: 2\times 40 = 80.
Therefore, when dividing 120 in the ratio 1:2 is 40:80.
Question
Share 518 in the ratio 2 : 5.
____ , ____
▶️Answer/Explanation
To share 518 in the ratio 2:5, we need to determine the amount each part represents.
In this ratio, the total number of parts is 2 + 5 = 7.
To find the value of each part, we divide 518 by the total number of parts:
Value of each part \(= \frac{518}{7}≈ 74.\)
Now, we can calculate the amounts for each part based on the ratio:
First part: \(2 \times 74 = 148.\)
Second part: \(5\times 74 = 370.\)
Therefore, when sharing 518 in the ratio 2:5, the first part is 148 and the second part is 370.
