Question
(a) Here are the first four terms of a sequence.
18 25 32 39
(i) Write down the next term.
(ii) Explain how you worked out your answer.
(b) The nth term of another sequence is \(n^2 + 3\).
Write down the first three terms of this sequence.
(c) Simplify.
(i) 6a + 5h − 4a − 8h
(ii) 5(x + 3) + 4(2x − 6)
(d) Factorise.
6g + 15
(e) A rectangle has length (x + 6) cm and width 5cm.
The area of this rectangle is 85cm2.
Find the value of x.
x = ………………………………………..
Answer/Explanation
Answer:
(a) (i) 46
(ii) Add 7 oe
(b) 4, 7, 12
(c) (i) 2a – 3h final answer
(ii) 13x – 9 final answer
(d) 3( 2g + 5) final answer
(e) 11 nfww
Question
(a) Multiply out the brackets and simplify.
5(2x + 3) -2(x + 4)
(b) (i) An equilateral triangle has side length 2x.
Write down an expression, in terms of x, for the perimeter of the triangle.
Give your answer in its simplest form.
(ii) A square has a perimeter of 20a.
Write down an expression, in terms of a, for the length of one side of the square.
Give your answer in its simplest form.
(c) The diagram shows a rectangle.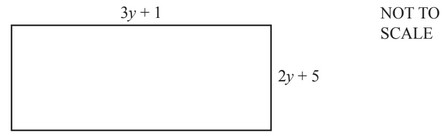
Find an expression, in terms of y, for the perimeter of the rectangle.
Give your answer in its simplest form.
(d) One mint costs m cents.
One toffee costs 6 cents more than one mint.
The cost of 3 mints and 7 toffees is 182 cents.
Write an equation, in terms of m, and solve it to find the cost of one mint.
Cost of one mint = ………………………… cents
Answer/Explanation
Ans:
(a) 8x + 7 final answer
(b) (i) 6x final answer
(ii) 5a final answer
(c) 10y + 12 or 2(5y + 6)
final answer
(d) 7(m + 6) + 3m = 182 or
7m + 42 + 3m = 182
14
Question
(a) Simplify.
4c+2d-c+6d
………………………………………….
(b) h=5m-2n
Calculate h when m = 4 and n = -6.
………………………………………….
(c) Solve.
7(x – 3) = 56
x = …………………………………………
(d) Make t the subject of the formula r = 6t + 7.
t = …………………………………………
(e) The diagram shows a triangle.
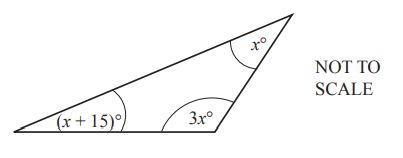
Use the diagram to write down an equation and solve it to find the value of x.
x = …………………………………………
Answer/Explanation
(a) 3c + 8d
(b) 32
(c) 11
(d) \(\frac{r-7}{6}\)
(e) 3x + x + x + 15 = 180 or better leading to [x = ] 33
