Question
(a) Here are the first four terms of a sequence.
18 25 32 39
(i) Write down the next term.
(ii) Explain how you worked out your answer.
(b) The nth term of another sequence is \(n^2 + 3\).
Write down the first three terms of this sequence.
(c) Simplify.
(i) 6a + 5h − 4a − 8h
(ii) 5(x + 3) + 4(2x − 6)
(d) Factorise.
6g + 15
(e) A rectangle has length (x + 6) cm and width 5cm.
The area of this rectangle is 85cm2.
Find the value of x.
x = ………………………………………..
Answer/Explanation
Answer:
(a) (i) 46
(ii) Add 7 oe
(b) 4, 7, 12
(c) (i) 2a – 3h final answer
(ii) 13x – 9 final answer
(d) 3( 2g + 5) final answer
(e) 11 nfww
Question
(a) These are the first four terms of a sequence.
–2 6 14 22
(i) Write down the next term.
(ii) Write down the rule for continuing the sequence.
(iii) Find an expression for the nth term.
(b) The nth term of another sequence is 5 1 ^n+ -h 6.
Write down the second term of this sequence.
(c) These are the first four terms of a different sequence.
–2 1 8 19
Write down the next term of this sequence.
Answer/Explanation
Ans:
(a)(i) 30
(ii) add 8 oe
(iii) 8n – 10 oe final answer
(b) 9
(c) 34
Question
(a) The diagram shows a rectangle with length 7a and width 2a.
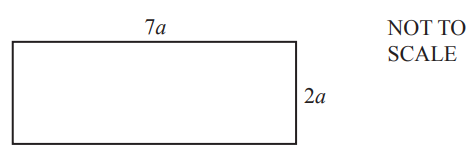
Write an expression, in its simplest form, for
(i) the perimeter,[2]
(ii) the area.[2]
(b) The nth term of a sequence is n2 + 5.
Find the first three terms of this sequence.
___ , ___ , ___ [2]
(c) (i) Complete the table of values for \(y=\frac{12}{x},x\neq 0.\)[3]

(ii) On the grid, draw the graph of \(y=\frac{12}{x}\) for \(-6\leqslant x\leqslant -1\) and \(1\leqslant x\leqslant 6\).[4]
(iii) On the grid, draw the line y = 8. [1]
(iv) Use your graph to solve \(\frac{12}{x}=8\).
x = [1]
Answer/Explanation
Ans:
5(a)(i) 18a final answer
5(a)(ii) 14a2 final answer
5(b) 6 9 14
5(c)(i) −4 −6 −12 6 4 3
5(c)(ii) Correct curve
5(c)(iii) Correct ruled line drawn
5(c)(iv) 1.3 to 1.7
